矩阵空间一类保持矩阵的秩1且保持体积不变的线性变换
陈荣群
(莆田学院基础教育学院,福建莆田351200
矩阵空间一类保持矩阵的秩1且保持体积不变的线性变换
陈荣群
矩阵体积是矩阵行列式绝对值的推广,也是向量长度的推广.在理解矩阵体积定义的基础上,研究了矩阵空间一类保持矩阵的秩1且保持体积不变的线性变换所满足的条件.
矩阵体积;保持秩1;线性变换;矩阵代数
矩阵体积的定义是在1992年由Adi Ben-Israel第一次提出,文[1]提出了每个矩阵都有相应的体积,并且应用矩阵体积来解决广义逆中的一些问题;在文[2-3]中利用矩阵体积的概念来处理各类曲线、曲面积分的计算问题,并给出了其在推广勾股定理、n维球面面积的计算以及概率中的应用.
线性保持问题主要是刻画保持一些不变量的线性算子的形式,在文[4-6]中,涉及到线性保持问题.现在来考虑保持矩阵体积不变的问题.那么对任意一个矩阵是否存在一个保持它的体积不变的线性变换?本文探讨矩阵空间一类保持矩阵的秩1且保持体积不变的线性变换所具备的形式.
1 预备知识
首先介绍矩阵体积及其相关的一些概念与符号.
设A∈Rm×nr(表示秩为r的m×n矩阵),r>0,约定:
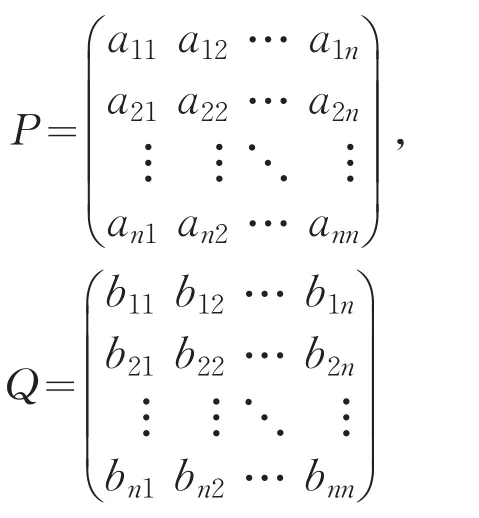
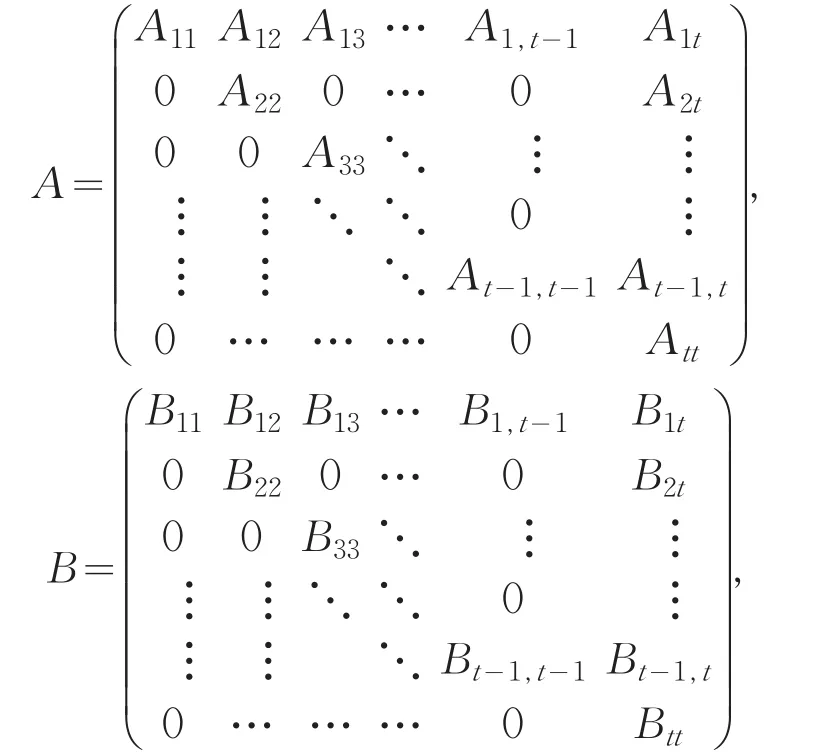
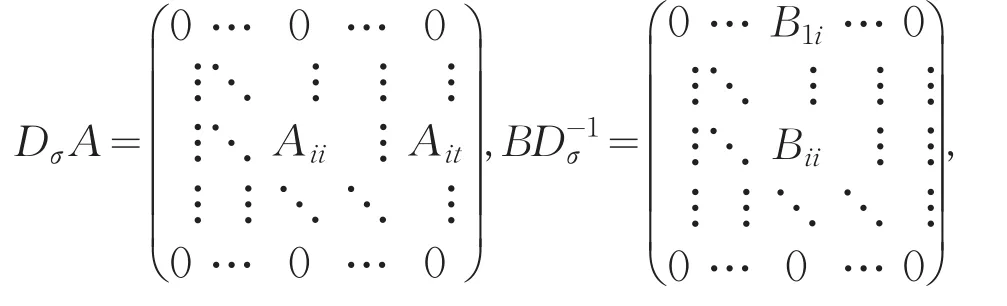
Qr,m={I={i1,…,ir}∶1≤i1 I∈Qr,m∶rankAI*=r表示A中最大的行线性无关集合的指标集.表示A中最大的列线性无关集合的指标集.表示A中最大的非退化子矩阵集合的指标集记Eij为(i,j)位置为1,其他位置均为0的n阶基本矩阵.Mn(F)是域上所有n阶矩阵构成的F一代数.定义1设矩阵的体积volA定义为:若r=0,volA=0;若r>0,则,约定.即表示A的所有非零r阶子式的平方和[1].定义2设(表示秩为r的复m×n矩阵集合),矩阵A的体积volA定义为:若r=0,则volA=0;若r>0,为了方便,约定.即表示A的所有非零r阶子式及其共轭乘积的和. 引理1对特征为0的代数封闭域C上矩阵代数Mn(C),如果φ是保持秩1的线性映射,那么任意一个矩阵A∈Mn() C,都存在可逆矩阵P,Q∈Mn() C,使或(A′是A的转置矩阵)[6]. 假设n是正整数n1,n2,…,nt也是正整数,使得n1+n2+…+nt=n,则称C={n1,n2,…,nt}是n的一个分解. 设F是一个域,对于n的每一个分解C,都对应着F中一个具有如下形式的n阶分块三角矩阵,这样的矩阵可构成一个F一代数Ω(C): 其中Aij是ni×nj矩阵块. 设C={n1,n2,…,nt}是n的一个分解,令C={nt,nt-1,…,n1}.如果σ是下标集合{1,2,…,t}的一个置换,令σ(C)={nσ(1),nσ(2),…,nσ(t)}. 引理3设C={n1,n2,…,nt},分别为n,m的分解,φ:分块三角矩阵Ω() C→Ω() C′是一个保持秩1的线性满射,那么n=m并且下列两种情况之一成立: (2)C=σ(C+)且,其中,其中 (a)A,B是Ω(C)中的满秩矩阵; (b)J是次对角线位置上的元素全是1,其它位置上的元素全是0的n阶矩阵; (c)σ是下标集合{1,2,…,t}满足下列条件的一个置换:σ(1)=1,σ(t)=t,nσ(i)=ni; (d)Dσ是由n确定的一个由t×t个矩阵块构成的n阶分块矩阵,其第σ(i)行第i列的块是一个nσ(i)阶单位矩阵,i=1,2,…,t,其余的块是零矩阵[6]. 定理1若φ是特征为0的代数封闭域C上矩阵代数Mn(C)的保持秩1的线性映射,则存在非奇异矩阵P,Q∈Mn() C,且P,Q满足两个条件:(1)P的每一列元素的平方和与Q的每一行元素的平方和的积都等于1;或P的每一行元素的平方和与Q的每一列元素的平方和的积都等于1;(2)P的任意不同的两列(行)的内积都等于0.使下面命题成立: (1)对任意的矩阵A∈Mn() C,有φ(A)=PAQ且volA=vol(PAQ)或φ(A)=PA′Q且volA=vol() PA′Q. (2)φ∶Mn(C)→Mn(C),A↦PAQ或A↦PA′Q是保持体积不变的线性变换. 证明(1)由引理1得:对矩阵代数Mn(C),如果φ是保持秩1的线性映射,那么任意一个矩阵A∈Mn() C,存在非奇异矩阵P,Q∈Mn() C,使φ(A)= PAQ或φ(A)=PA′Q. 下面对φ(A)=PAQ的情况进行讨论,对φ(A)= PA′Q的情况利用矩阵的性质也可得到相应的结论. 一方面,设 则易知P,Q不为零矩阵.由于rank(PAQ)=rank(A)= 1,令A=Eij,所以 另一方面, 故 上面只对矩阵的行式的情况进行讨论,利用矩阵列式的性质也可得到相应的结论. 将(1)用线性变换来刻画,即得到(2). 所以上述命题成立.证毕. 推论若φ是域C上n阶上三角矩阵空间Tn(C)的保持秩1的线性变换,则上述结论对n阶上三角矩阵空间Tn(C)也成立. 定理2设φ是分块三角矩阵Ω() C→Ω() C′是一个保持秩1的线性满射,对任意的分块三角矩阵T∈Ω() C,volT=1,则存在非奇异矩阵A,B∈Ω() C且A,B满足两个条件: (1)Aii的每一列元素的平方和与Bii的每一行元素的平方和的积都等于1;或Aii的每一行元素的平方和与Bii的每一列元素的平方和的积都等于1; (2)Aii的任意不同的两列(行)的内积都等于0(1,2,…,t);当n=m时,下面命题成立. 证明(1)由引理3得:若φ是矩阵代数Ω(C)的保持秩1的线性映射,则对任意的分块三角矩阵T∈Ω() C,存在非奇异矩阵A,B∈Ω() C,使φ(T)=或 一方面,设 则易知A,B不为零矩阵. 其中Dii是ni×ni单位矩阵块,即其 中Tii是ni×ni矩阵块. 由于 由定理1得,Aii与Bii必须满足两个条件(1)Aii的每一列元素的平方和与Bii的每一行元素的平方和的积都等于1;(2)Aii的任意不同的两列的内积都等于0; 上面只对矩阵的行式的情况进行讨论,利用矩阵列式的性质也可得到相应的结论. 将(1)用线性变换来刻画,即得到(2). 所以上述命题成立.证毕. [1]Ben-Israel A.A volume associated withmatrices[J].Lin⁃ear Algebra and its Applications,1992(167):87-111. [2]Ben-Israel A. The change of variables formula using matrixvolume[ J ]. SIAM. J. Matrix Analysis,1999(21):300-312. [3]Ben-Israel A. An application of the matrix volume in proba⁃bility[ J ]. Linear Algebra and its Applications,2001(321):9-25. [4]Ben- Israel B. Generalized inverses:theory and applications[M]. Berlin-Heidelberg-New York: Springer-Verlag,2002. [5]Botta P. Linear maps preserving rank less than or equal toone[ J ]. Linear and Muhilinear Algebra,1987,20:197-201. [6]黄冲,曹佑安. 一类分块三角矩阵代数的保持秩1 的线性满射[ J ]. 湘潭大学学报:自然科学版,2003,25(3):6-11. [7]李明,方宜. 矩阵的体积及其应用[ J ]. 西北师范大学学报:自然科学版,2005,41(6):86-90. [2] [3] [4] [5] [6] [7] Ben-Israel A.The change of variables formula using matrix volume[J].SIAM.J.Matrix Analysis,1999(21):300-312. Ben-Israel A.An application of the matrix volume in proba⁃bility[J].Linear Algebra and its Applications,2001(321):9-25. Ben-Israel B.Generalized inverses:theory and applications [M].Berlin-Heidelberg-New York:Springer-Verlag,2002. Botta P.Linear maps preserving rank less than or equal to one[J].Linear and Muhilinear Algebra,1987,20:197-201.黄冲,曹佑安.一类分块三角矩阵代数的保持秩1的线性满射[J].湘潭大学学报:自然科学版,2003,25(3):6-11.李明,方宜.矩阵的体积及其应用[J].西北师范大学学报:自然科学版,2005,41(6):86-90. 责任编辑:毕和平 The Linear Transformation of Preserving Matrix Rank One and Constant Volume on Matrix Space CHEN Ronqun The volume of matrix is a generalization of the determinant,also a generalization of the vector length.Based on the understanding of the definition of the matrix volume,the linear transformation with the conditions of preserving matrix rank 1 and constant volume is studied on matrix space. volume of matrix;preserving matrix rank 1;linear transformation;matrix of algebra O 151.21 A 1674-4942(2014)04-0373-04 2014-06-19



2 主要结论及证明


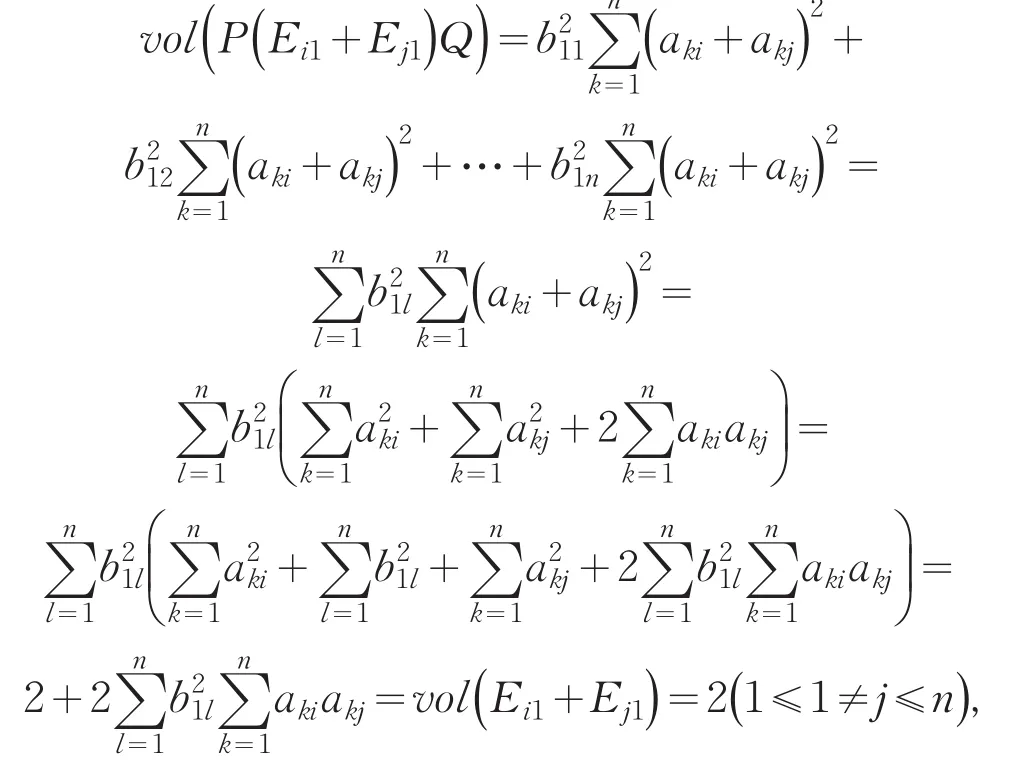




(College of Basic Education,Putian University,Putian 351200,China)

