Logistic模型参数估计研究
姜爱平,郝慧娟
(1.宁夏大学数学计算机学院,宁夏银川750021;20宁夏大学民族预科学院,宁夏银川750021
Logistic模型参数估计研究
姜爱平1,郝慧娟2
(1.宁夏大学数学计算机学院,宁夏银川750021;20宁夏大学民族预科学院,宁夏银川750021
logistic模型的应用非常广泛.其模型参数是影响精度的重要因素之一,文章在现有文献基础上,提出一种新的改进方法,即牛顿插值法和最优权重法对模型参数进行估计.实例分析表明,该方法在一定程度上提高了模型相关系数,降低了模型偏差,且具有较为理想的预测效果.
logistic模型;参数估计;牛顿插值
Logistic模型又称阻滞增长模型,不仅可以描述生物增长规律[1-3],也适用于描述耐用消费品拥有量增长规律[4],而模型参数是影响模型精度的重要因素之一.关于参数a和r,大多采用最小二乘法,即RSS准则进行估计[5-8].对于饱和值的K估计,一般要求数据为等间距时间序列,显然很多实验数据不能满足此要求.即使数据为等间距序列,在选取中间数据时,由于存在人为因素,模型误差波动性较大.文献[6]在对饱和值K进行估计时,采用几何平均法进行取值,该方法简单易懂但较为粗糙.文献[7-8]采用交替迭代法对未知参数进行估计,虽模型精度理想,但计算量大且公式复杂.文献[5]采用差商近似导数方法和数据拟合的思想,对未知参数a和r进行估计时,对向前差分本文采用牛顿插值法和最优权重法对模型未知参数进行估计,研究表明该建模方法预测效果理想,同时也为参数估计研究提供参考.
1 logistic模型理论介绍
Logistic模型由比利时数学家Verhulst于1840年在malthus模型基础上提出,其形式为

2 模型参数估计
2.1 值的估计
当原始数据为非等间距序列时,由于三点法要求数据满足t1+t3=2t2,这在实际数据中常常不能实现,故这里采用插值法求出中间数据来解决此问题.根据logistic曲线函数性质可知,在拐点处,有,即,因此,只要知道曲线的拐点以及的值,便可根据上式求出参数K的估计值.这里采用牛顿插值法计算拟合曲线的拐点t*及定义称为函数f(x)关于点x0,xk的一阶均差.

称为函数f(x)的二阶均差.
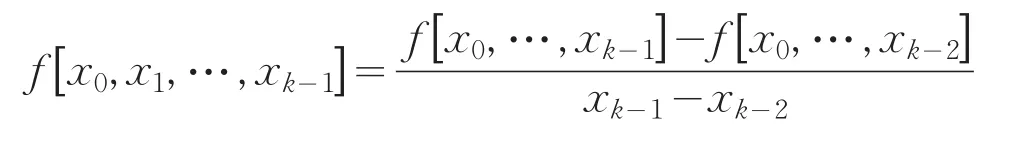
为函数f(x)的k-1阶均差.

为函数f(x)的k阶均差.
假设x是[a,b]上一点,由Newton插值公式可得

只需把后式代入前式,便得
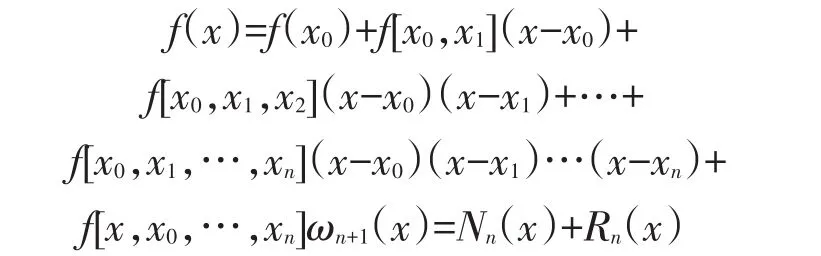

Newton均差插值多项式为

把(t,Δx(t)/Δt)作为插值节点,求出插值曲线拐点t*,利用插值公式求出的值,从而求得的估计值为x(t*).


具体步骤如下:


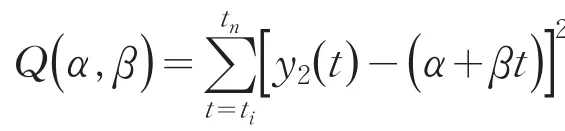
3 算例分析
算例1引用文献[6]中例子,即蓟马产卵实验数据进行分析,计算结果详见表1,表2.
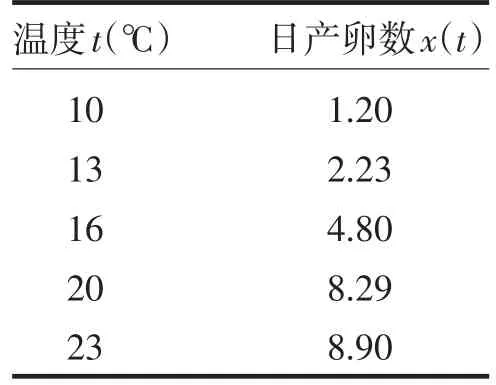
表1 蓟马产卵实验数据Tab.1Experimental data of thrips laying eggs

表2 模型结果比较Tab.2Comparison and analysis of model
由上述结果可知,由于三点法所选数据满足t1+ t3=2t2,这里选取x(10),x(20)作为始点和终点,运用牛顿插值法求出当t=15时,x(15)的值.利用公式求出环境最大容量K值.比较上述三种方法发现,运用插值法,直接求出模型拐点这种方法,具有最小均方误差和最大相关系数的优点.
算例2引用文献[5]的例子,即城镇居民家庭彩色电视机平均每百户拥有量数据进行分析对比研究,根据RSS准则求出最优权重ω=0.38,计算结果详见表3,表4.
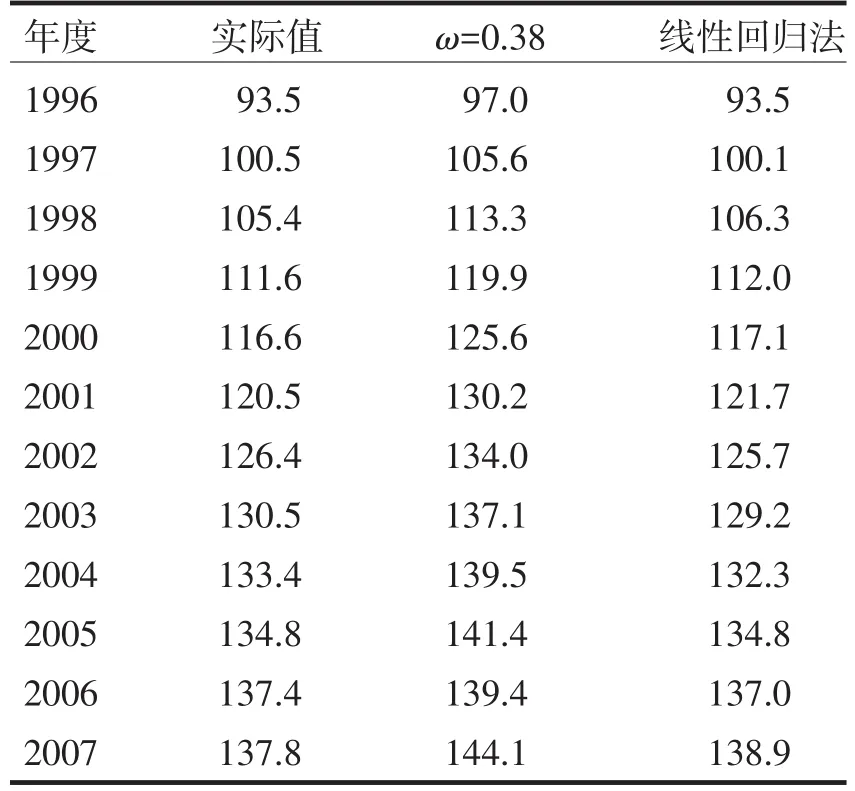
表3 模型预测结果Tab.3The prediction result of model

表4 模型结果比较Tab.4Comparison and analysis of model
由上述结果可知,在差商近似导数方面,对于向前差商和向后差商,采用不同权重在一定程度上提高了模型相关系数,同时降低模型偏差.对于文献[5]中的例子,采用牛顿插值拐点法分析发现,城镇居民百户电视机拥有量增长变化率在1992年—1993年达到最大,此后变化率逐渐减少.根据logistic曲线几何性质可知,该拟合曲线的饱和,通过模型拟合验证了其合理性,同时完善了文献[5]中的相关结论.
4 结论
关于logistic模型参数K的估计,本文采用牛顿插值拐点法,求出曲线的拐点,结合模型相关系数,对估计值进行修正.实例表明,该方法在一定程度上提高了模型相关系数R值,同时具有较小的模型偏差.对于参数a和r的估计,针对向前差商和向后差商,通过赋予不同的权重来提高模型的相关系数,降低模型偏差,使得模型具有较高精度.但与线性回归法相比,误差较大.其主要原因在于差商近似导数时存在系统误差,即或者成立的前提是Δti→ 0,事实上,这是一个很苛刻的条件,因为实际问题中常常不能满足此要求.
[1]黄润龙,帅友良.人口增长的logistic模型及其应用研究[J].南京人口管理干部学院学报,2000,16(3):24-27.
[2]郭石磊,王云鹏.改进的logistic模型预测人口数量[J].宁波职业技术学院学报,2010,14(2):44-45.
[3]王勇.logistic人口模型的求解问题[J].哈尔滨商业大学学报,2006,22(5):58-59.
[4]何文章,张宪彬.利用logistic模型预测耐用消费品社会拥有量[J].数理统计与管理,1994,13(1):21-25.
[5]范国兵.一种估计logistic模型参数的方法及其应用实例[J].经济数学,2010,27(1):105-110.
[6]殷祚云.logistic曲线拟合方法研究[J].数理统计与管理, 2002,21(1):41-46.
[7]杨昭军,师一民.logistic模型参数估计及预测实例[J].数理统计与管理,1997,16(3):13-15.
[8]苑延华.关于logistic模型参数估计的比较[J].黑龙江科技学院学报,2008,18(6):474-477.
责任编辑:毕和平
Research on Parametric Estimation of Logistic Model
JIANG Aiping1,HAO Huijuan2
(1.School of Mathematics and Computer Science,Ningxia University,Yinchuan 750021,China;2.School of Ethnic Preparatory Education,Ningxia University,Yinchuan 750021,China)
The logistic model is also called block growth model,its application is very wide.The model parameters is one of the important factors affecting accuracy.In this paper,based on the existing literature,a new method was put forward, namely the Newton interpolation method and the optimal weighting method for model parameter estimation.The analysis shows that it can improve the correlation coefficient,reduce the error,and has satisfactory forecast results.
logistic model;parametric estimation;Newton interpolation
C924.2
A
1674-4942(2014)04-0360-03
2014-09-02
宁夏大学科学研究基金(ZR1332)

