复发事件下一般混合治愈模型
曾小凤,陈传钟,李霓
(海南师范大学数学与统计学院,海南海口571158
复发事件下一般混合治愈模型
曾小凤,陈传钟,李霓*
(海南师范大学数学与统计学院,海南海口571158
在复发事件数据的半参数比率模型基础之上,利用调整后的logistic模型回归治愈率部分,提出一类可将一般比率模型包括在内的混合治愈模型,从而刻画协变量对事件复发率的影响.同时给出该模型中未知参数的估计方法,证明这些估计的相合性和渐近正态性.
复发事件;半参数比率模型;治愈率;Logistic模型;估计方程
近几十年里,由于医学统计的迅猛发展,生存分析模型理论及方法的研究便得到不断推广及深入.许多模型在实际问题的背景下不断被提出,如脆弱模型、混合治愈模型等,同时各类估计方法也得到了构造.另一方面,人们在生存分析中开始研究同一个实验对象疾病多次复发的情况[1].描述这类情况的数据称为复发事件数据(Recurrent Event Data).对于此类数据的研究,国内的成果还比较少.因为其特有的数据结构和广泛的应用价值,所以已吸引了诸多国家的关注,它的研究除了重要的理论意义外,直观且深远的应用价值更是不可忽略[2].
本文对复发事件数据的符号假设与文[3]一致.记N*(t)为在区间[0,t]上所发生的事件的次数,如果E{dN*(t)}=μ(t)dt,那么μ(t)称为N*(t)的比率函数.并且这里dN*(t)=N{(t+dt)-}-N*(t-)为在[t,t+dt)上的增量(当dt→0).假设在一定时间内,有n个研究个体,且每个个体之间是相互独立的.N*i()∙记为个体i(i=1,...,n)在时刻t所经历事件的次数.但在实际研究及应用中,通常N*i()·不能够完整观测.记Ci是第i个个体的删失时间,可收集的复发事件数据为Ni(t)=.设Xi(t)表示协变量,并假设在给定)条件,删失时间Ci与相互独立,即


其中γ0为未知的回归参数向量未知的基本比率函数.关于模型(1)的研究:Pepe和给出了γ0估计大样本理论,但是证明方法较为粗糙;Lawless等[5]在离散时间条件下,研究γ0和λ0(t)的估计及估计的渐近性;Lin等[6]改进了Lawless等的估计,并构造了均值函数的置信区间.
生存分析数据中,已有学者对治愈个体做了研究.Boag[7]最早提出了混合治愈模型的概念,并对治愈率和未治愈病人的存活率给出了估计方法.Fare⁃well[8]发展Cox比率模型,用Cox模型来刻画生存函数部分,说明其中有治愈现象的存在.同时用Logis⁃tic及Cox比率模型对治愈者的治愈率及未治愈者的风险函数研究.但是,在复发事件数据中,研究个体多数被假设为一直反复发病,没有治愈个体的存在.因此在复发事件数据中发展新模型十分需要.
1 模型和估计方法
1.1 一般混合治愈模型
对复发数据中对识别治愈者问题,假设在一定时间内,研究个体i共个有n个(i=1,2,...,n),并且每个个体之间是相互独立的.W(t)和X(t)都表示与复发率有关协变量,W(t)通过治愈率间接影响复发率,X(t)通过经典的比率模型(式(1))直接影响复发率,它们是不同的两部分协变量.N*(t)为在时间t或之前拥有事件次数这样的计数过程.但是在有限时间内,不能够完全观察,记C为删失时间,可设N(t)=N*(min(t,C)),N(t)为可观测到的数据.
π表示个体被治愈的概率,(1-π)表示个体未被治愈的概率.设当个体是治愈者时,复发率为0;而当个体是非治愈者时,其部分协变量对复发率的影响用模型(1)比率函数表示,还有部分协变量通过调整后的logistic模型影响治愈率来影响复发率.
故考虑如下,一般混合治愈模型:

这里π(W(t))表示第i个研究个体被治愈的概率,它与协变量Wi(t)有关,并且二者关系用上面的调整后的logistic模型(式3)回归.其中β0,γ0为未知的回归参数向量,分别表示协变量Wi(t)与Xi(t)对复发事件比率的影响,λ0(·)是未知的基本比率函数.V是一个权重,当V=0时,模型(2)和(3)就退化成(1).因此我们的模型是一类,可将一般比率模型包括在内的混合治愈模型.
1.2 模型的估计方法




2 统计性质
在研究渐近性质之前,先给出复发事件数据的一般结构:
(Δ1){Ni(·),Xi(·),Wi(·),Ci},(i=1,2,...,n)独立同分布.
(Δ2)P(Yi(τ)=1)>0,且几乎处处Ni(τ)<η<∞,i= 1,2,...,n,其中η为常数.
(Δ3)Wi(·)和Xi(·)每一个分量函数的总变量分别以一个非随机常数为界.
(Δ4)A为非奇异矩阵,其中
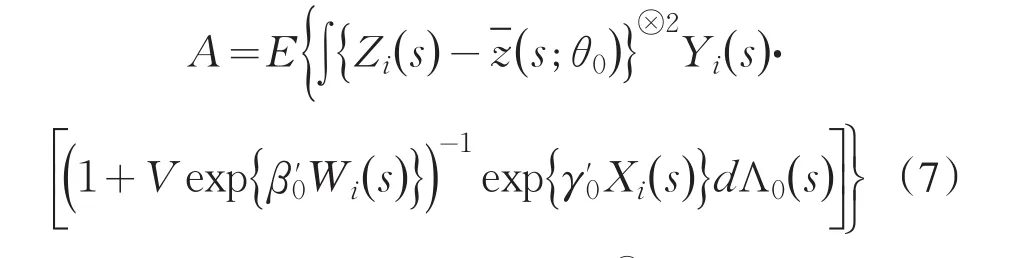
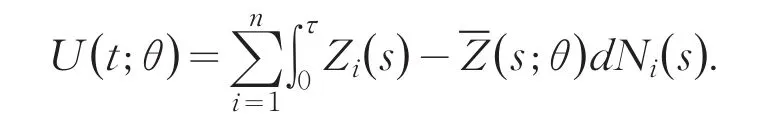
接下来给出这些前面估计的渐近性质.

从一致强大数定律及文[6]中的引理1知道,ξ(s;t)的相合估计为ξ(s;t),这里,
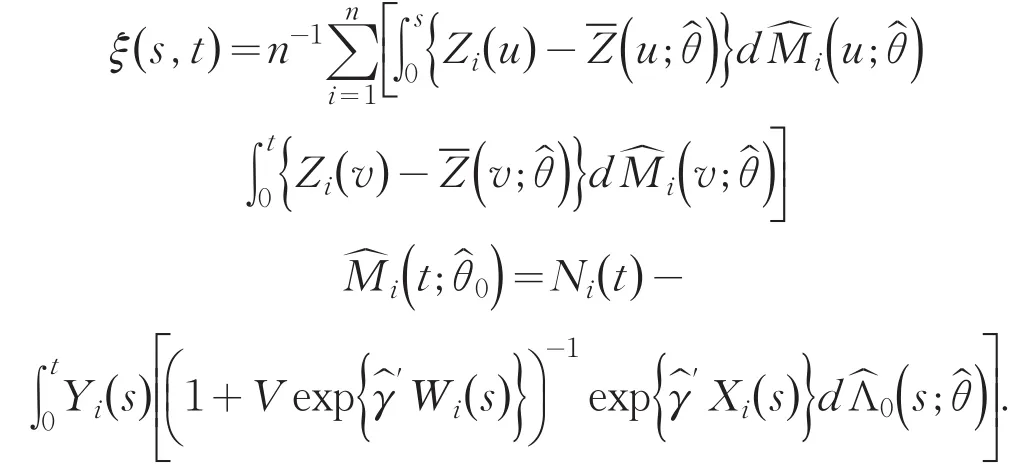
证明由于

则有

其中

类似于文[6]中附录A.2的证明,知道n-1/2U(t;θ0)是弱收敛的,并且其极限分布是均值为0,协方差函数在式(8)中给出.


则有
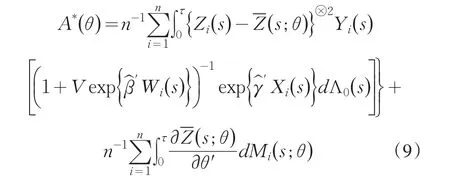
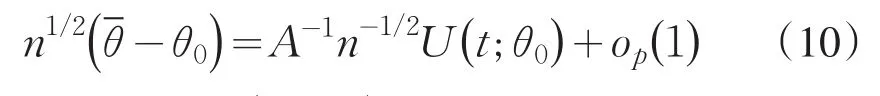

未知量被估计量替代,可以得到协方差Γ(s,t)函数的一个相合估计是

这里

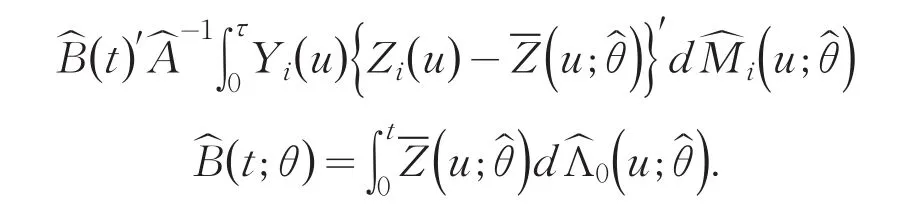

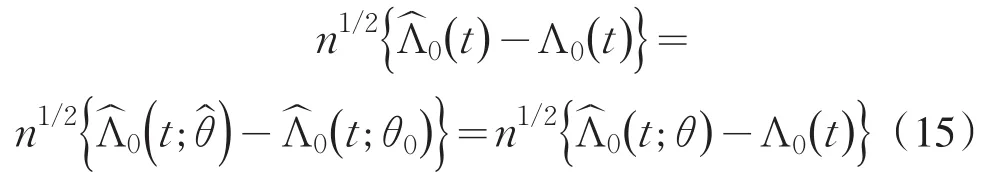

由[6]中的引理1以及一致强大数定理知,几乎处处

其中B(t;θ0)由式(10)给出.由性质(7)和式(10)有

另一方面,对于0≤t≤τ可以得到

于是利用文[6]中的引理1知,对t一致有

最后由式(15)和式(16)知,对t一致有

[1]Andersen P K, Gill R D. Cox's regression model counting process: A large sample study[ J ]. Annals of Statistics,1982, 10,1100-1120.
[2]刘焕彬,苗瑞,孙六全. 有偏抽样下带信息观察和删失的面板数据的统计分析[ J ]. 中国科学A 辑:数学,2011,41(4): 365-376.
[3]戴家佳,孙六全,杨振海. 复发事件下加性乘积比率回归模型[ J ]. 中国科学A 辑:数学,2009,39(5):605-613.
[4]Pepe M S, Cai J. Some graphical displays and marginal regres⁃sion analyses for recurrent failure times and time-dependent covariates[ J ]. J Amer Statist Assoc,1993,88:811-820. [5]Lawless J F, Nadeau C. Some simple robust methods for the analysis of recurrent events[ J ]. Technometrics,1995,37:158-168.
[6]Lin D Y, Wei L J, Yang I, et al. Semiparametric regression for the mean and rate functions of recurrent events[ J ]. J Roy Statist Soc Ser B,2000,62(4):711-730.
[7]Boag J W. Maximum likelihood estimates of the proportion of patients cured by cancer therapy[ J ]. Journal of the Royal Statistical Society Series B (Methodological),1949,11(1):15-53.
[8]Farewell V T. The use of mixture models for the analysis of survival data with long-term survivors[ J ]. Biometrics,1982, 38:1041-1046. [9]
Lin D Y, Ying Z L. Semiparametric analysis of general addi⁃tive-multiplicative hazard models for counting processes[ J ]. Ann Statist,1995,23(5):1712-1734.
责任编辑:毕和平
General Mixture Rate Model for Recurrent Event Data
ZENG Xiaofeng,CHEN Chuanzhon,LI Ni*
(College of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China)
In this paper,on the basis of semiparametric rate models for recurrent events data,using the cure rate of adjust⁃ed Logistic regression model,a mixture rate model including general rate model is proposed,to depict covariate's impact on the recurrence rate.For inference about regression parameters,estimating equation approaches are developed and asymptot⁃ic properties of the proposed estimators are established.
Recurring event;Semiparametric rate model;Cure rate;Logistic model;Estimating equation
O 212
A
1674-4942(2014)04-0365-04
2014-06-21
海南省教育厅高等学校科学研究项目(Hjkj2013-16);海南师范大学博士启动基金项目;海南师范大学研究生创新科研项目(Hsyx2014-34)
*通讯作者

