狄氏空间上的有界线性映射
王玮,马丽,韩新方
(海南师范大学数学与统计学院,海南海口571158
狄氏空间上的有界线性映射
王玮,马丽,韩新方*
(海南师范大学数学与统计学院,海南海口571158
建立了非对称狄氏型狄氏空间到其对称型狄氏空间上的一种映射,证明了该映射及其拟映射都是有界的线性映射,并且给出了在此映射下狄氏空间中元素对应关系和表达式.
对称狄氏型;非对称狄氏型;对应关系;映射;有界线性映射
设(E,β(E))为一个可测空间,m是(E,β(E))上的δ-有限测度,以(,)来记L2(E,m)上的内积.用(ε,D(ε))表示L2(E,m)的狄氏型,狄氏型的定义见文[1-3].若这个狄氏型满足ε(u,v)=ε(v,u),∀u,v∈D()
ε,则称此狄氏型为对称狄氏型.对称狄氏型与非对称狄氏型有很大的区别,如正则对称狄氏型联系着一个Hunt过程,而正则非对称狄氏型则联系着一对对偶的Hunt过程;对称狄氏型有漂亮的Beurling-Deny分解和Lejan变换公式,非对称狄氏型虽然也有Beurling-Deny分解,但要相对复杂一些,要用到S.P.V.可积来描述跳部分,而强局部部分分成两块,一块满足Lejan公式,另一块不对应着测度,只能通过算子来定义,此算子满足一定的变换公式,详细的结果见文[4].如果能在非对称狄氏型和对称狄氏型之间建立某种对应关系,则研究非对称狄氏型时,可以借助于这种对应关系,研究相应的对称狄氏型.基于这种考虑,本文针对非对称狄氏型定义域中元素和其对称型定义域中的元素之间的对应关系作了一些探讨.
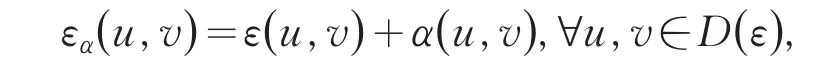
文[5]中引理2.1用Riesz表示定理,得到了如下结果:设,则存在唯一的,且对有
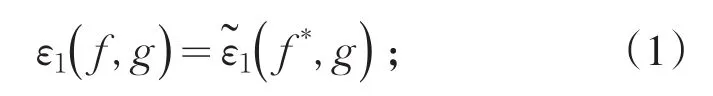



下证算子φ的有界性.对∀f∈D()ε有
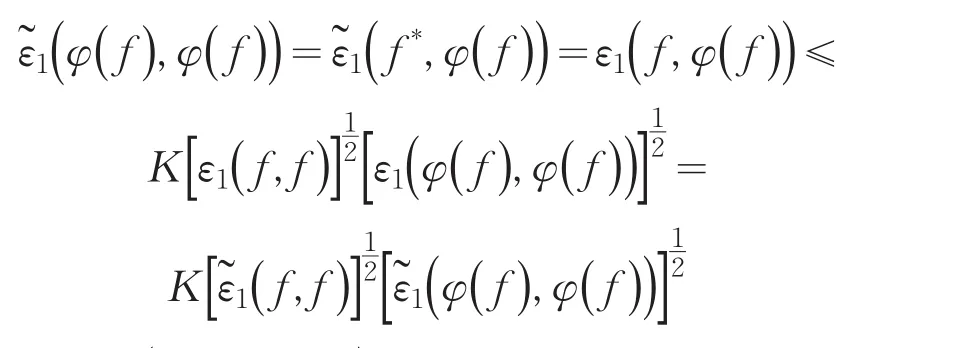
对任意的实数a,b,任意的f1,f2,g∈D()ε有


(3)对∀f,g∈D()ε有
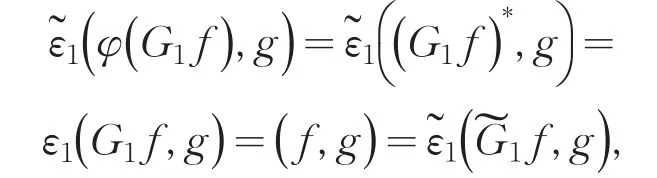
(4)由非对称狄氏型的预解方程知:对任意的α,β>0有,Gαf-Gβf=(β-α)GαGβf=(β-α)GβGαf,所以对∀g∈D()ε有
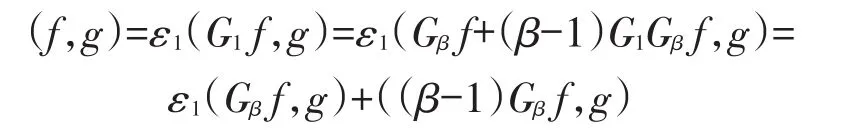
所以
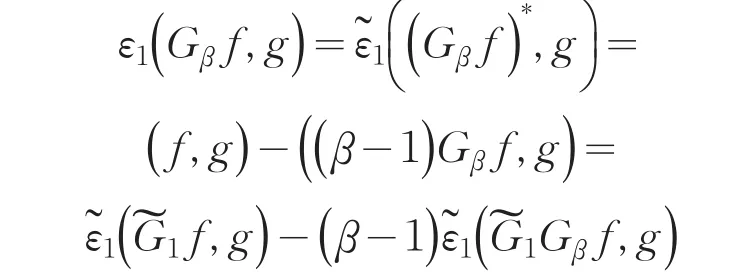
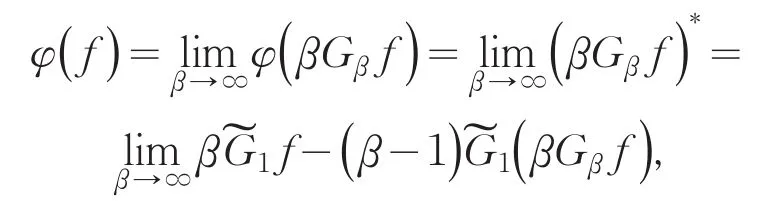
[1]Fukushima M,Oshima Y,Takeda M.Dirichlet forms and symmetric Markov processes[M].(Second version),Walter de Gruyter,2011.
[2]马志明.狄氏型(Dirichlet Form)简介[J].重庆师范学院学报:自然科学版,2001,18(1):1-7.
[3]Ma Z M,Rockner M.Introduction to the theory of(nonsymmetric)Dirichlet form[M].Springer-Verlag,1992.
[4]Hu Z C,Ma Z M,Sun W.On representations of non-sym⁃metric Dirichlet forms[J].Potential Anal,2010,32:101-131.
[5]Chen C Z,Ma L,Sun W.Stochastic Calculus for Markov Processes Associated with Non-symmetric Dirichlet Forms [J].SCIENCE CHINA Mathematic,2012,55(11):2195-2203.
责任编辑:毕和平
The Bounded Linear Mappings on Dirichlet Space
WANG Wei,MA Li,HAN Xinfang*
(College of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China)
This paper constructs one relationship between the functions in the domain of non-symmetric Dirichlet form and its symmetric part and proves that the mapping-relationship has inverse mapping which are both linear bounded mapping on the Dirichlet space.
symmetric Dirichlet form;non-symmetric Dirichlet form;correspondence;the mapping;bounded linear map⁃ping
O 211.1
A
1674-4942(2014)04-0363-02
2014-07-05
国家自然科学基金(11201102,11361021,11326169);海南省自然科学基金(112002,113007)
*通讯作者

