管材弯曲中应力中性层位移计算与影响因素分析

贾美慧，唐承统，刘检华

（北京理工大学 先进加工技术国防重点学科实验室，北京 100081）

管材弯曲中应力中性层位移计算与影响因素分析

贾美慧，唐承统，刘检华

（北京理工大学 先进加工技术国防重点学科实验室，北京 100081）

为研究管材弯曲成形过程中应力中性层位移及影响因素，基于塑性力学全量理论，分析了管材弯曲的应力应变规律，在考虑材料硬化特性和壁厚变化的情况下推导出应力中性层位移的近似计算公式，并利用正交设计法对应力中性层位移的影响因素进行了敏感性分析，认为相对弯曲半径和硬化指数是影响应力中性层位移最敏感的因素，其它参数无显著影响．通过与数值模拟结果对比，证明了理论分析的正确性和有效性．

管材弯曲；应力中性层；正交设计；敏感性分析

弯管零件作为量大面广的关键轻量化构件，在航空航天、船舶、汽车和能源等高技术产业得到了日益广泛的发展和应用［1］．由于管材的弯曲成形是一个多因素耦合作用的复杂变形过程，再加上管材中空结构的特点，使得变形过程中极易产生回弹、壁厚减薄甚至拉裂、起皱等质量缺陷，因此国内外学者针对管材弯曲成形机理、成形质量预测以及工艺参数优化等，展开了诸多研究［2－5］．管材弯曲成形主要表现为外侧材料受拉伸长，内侧材料受压缩短，在拉应力向压应力过渡的区域存在一个应力中性层．应力中性层位置以及影响因素的确定对于深入掌握管材弯曲成形机理具有重要的理论意义．

目前，有关应力中性层的研究多以板材［6－7］为主，而针对管材弯曲过程中产生的应力中性层位移却少有研究．N．C．Tang［8］推导了管材中性层位移的近似计算公式，但其采用的是理想弹塑性模型，没有考虑材料硬化特性对应力中性层位移的影响．文献［9］对应力中性层和应变中性层的位置进行了初步讨论，但未对其影响因素进行研究．

本文针对管材弯曲过程中应力中性层位移的问题，基于塑性力学全量理论，通过分析管材弯曲过程中的应力应变状态，推导了考虑材料特性的应力中性层位移近似计算公式，并结合正交设计方法对其影响因素进行了敏感性分析，获得了对应力中性层影响显著的参数以及影响规律．

1 管材弯曲变形应力应变分析

管材在外力矩M作用下发生纯弯曲变形，外侧材料受拉伸长，管壁减薄，内侧材料受压缩短、管壁增厚．相关几何参数如图1所示，其中t1为管材外侧减薄后的壁厚，t2为管材内侧增厚后的壁厚，r为管材外半径，R为弯曲半径，α为任意点处的横截面扇角，Hσ为应力中性层位移，ασ为应力中性层偏移角．管材弯曲时主要受切向拉应力σθ1、切向压应力σθ2以及周向应力σα1和σα2为简化分析，提出三个基本假设：

1）平截面假设，弯曲后管材横截面仍保持为平面；

2）忽略管材沿壁厚方向的径向压力，即σt＝0；

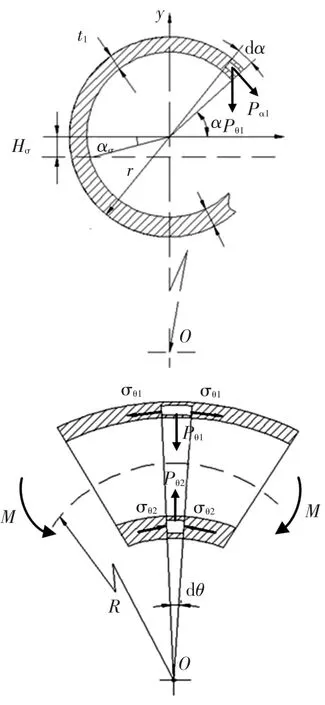
图1 管材弯曲应力状态示意图

1．1 应力状态分析

管材在外弯矩M作用下，外侧纤维受拉应力σθ1作用，产生指向弯曲中心的合力d Pθ1

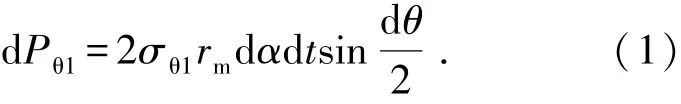
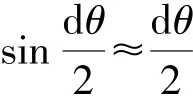
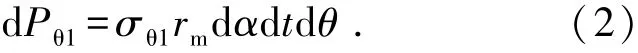
在管材弯曲横截面内，切向拉应力为第一主应力，其合力．d Pθ1产生的沿圆周方向的分力为

为描述切向应力σθ1与周向应力σα1之间的关系，d Pα1又可表示为

联立式（2）、（3）、（4）可得

对式（5）在（0，α）上进行积分并化简，令m＝R/rm，得到外侧受拉区周向应力的分布函数

同理，管材内侧受到压应力σθ2，其在圆周方向的分力为

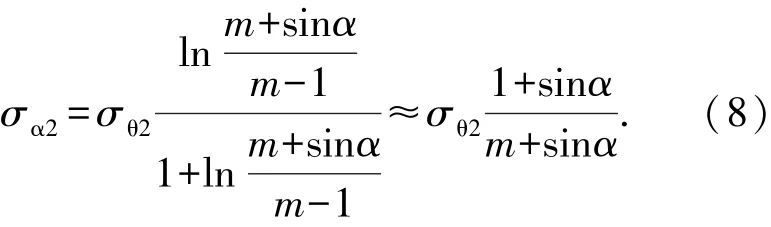
1．2 应变状态分析

管材弯曲变形的主要表现形式是应变中性层外侧材料受拉伸长，内侧材料受压缩短，因此切向应变为第一主应变，但是随着塑性变形程度的不断增强，管径变小、外侧壁厚减薄、内侧壁厚增厚，管材的三向应变状态越来越明显．因此管材弯曲三向应变可描述为

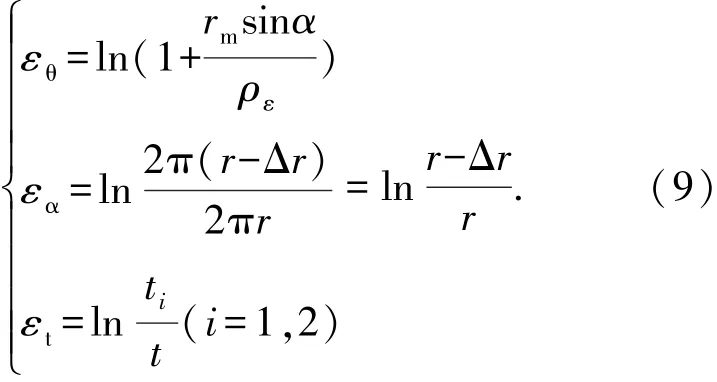
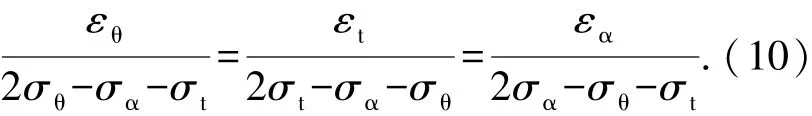
联立式（6）、（9）、（10），得到管材外侧周向应变εα1和径向应变εt1

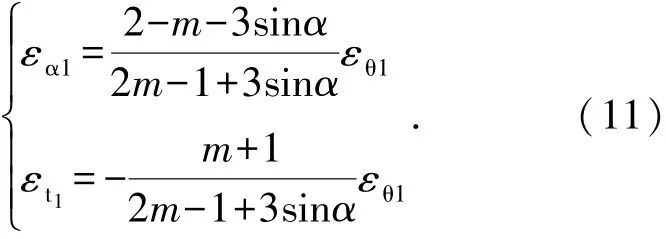
同理，联立（8）、（9）、（10），得到管材内侧周向应变εα2和径向应变εt2

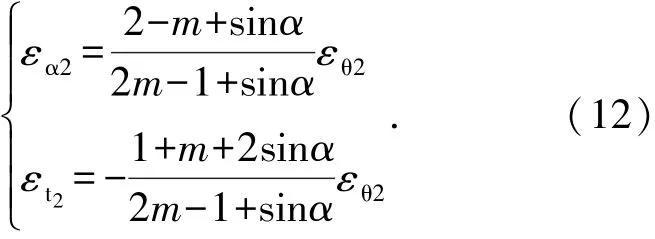
由式（9）、（11）、（12）可推导出变形后的外侧壁厚t1和内侧壁厚t2的计算公式

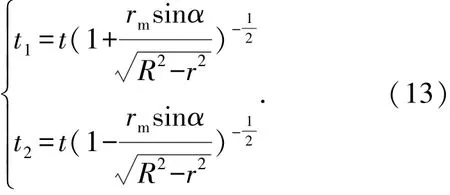
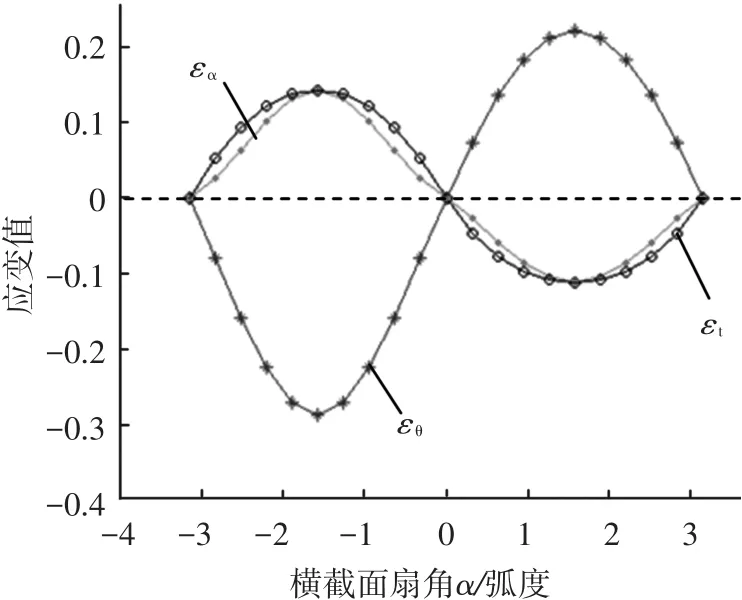
图2 管材弯曲应变周向分布图

2 应力中性层位移计算

由于管材外侧切向拉应力小于内侧切向压应力，且外侧壁厚减薄、内侧壁厚增厚，导致外侧切向拉应力作用面积小于内侧压应力作用面积，因此为使内部力矩平衡，应力中性层必然产生偏移．根据轴力平衡条件，有

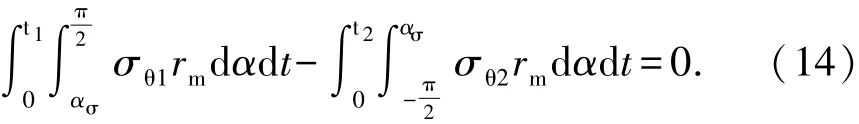
将式（6）、（8）、（11）和σt＝0代入Mises屈服准则定义的等效应力和等效应变的表达式

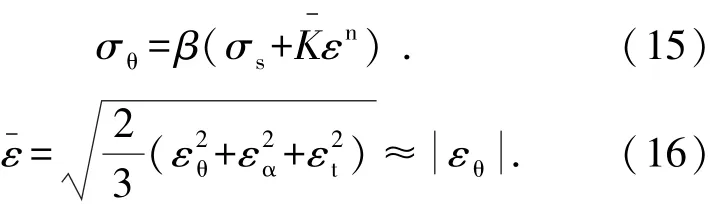
将式（15）、（16）代入式（14）并积分，得到应力中性层偏移角ασ的近似计算公式

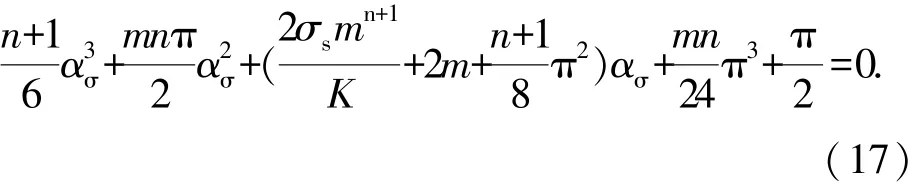
采用Matlab可对式（17）进行求解，得到应力中性层偏移角ασ，进而求得应力中性层位移Hσ＝r sinασ，显而易见，对于相同材料参数以及相同弯曲半径的管材，管径越大，其应力中性层位移Hσ也越大．

3 影响因素敏感性分析

敏感性分析是系统分析中分析系统稳定性的一种方法，其局限性在于不能明确指示某个因素的变动对系统稳定性影响的大小．而正交设计法是一种研究多因素、多水平的试验设计方法，它不仅具有数据点“均匀分散，齐整可比”的优点，而且可以通过方差分析、极差分析等获得更多有价值的结论．因此引入正交设计方法对系统进行敏感性分析更符合实际情况［11］．

式（17）表明，应力中性层位移主要受相对弯曲半径R/D、屈服极限σs、塑性系数K、硬化指数n四个因素的影响，根据航天常用管材1Cr18Ni9Ti、T2以及5A06等管材的拉伸实验所得性能参数初步确定各材料参数取值范围，相对弯曲半径取值则以常用弯曲半径要求为参考，选取L16（45）正交表，因素水平表如表1所示．

表1 因素水平表

选取显著性水平α＝0．05，选择空白列作为误差列，得到方差分析表如表2所示．

由表2方差分析可知，相对弯曲半径和硬化指数对应力中性层位移的影响最为显著，其它参数的影响很小，各因素对应力中性层位移影响趋势分析如图3所示．横坐标为各因素分类，其水平值由小到大排列，纵坐标为反映应力中性层位移Hσ大小的统计参数．

表2 方差分析表

由图3中Hσ＜0可知，在管材弯曲过程中，应力中性层向弯曲中心方向产生了移动，其位移Hσ随R/D和σs的增大而减小，随n和K的增大而增大．

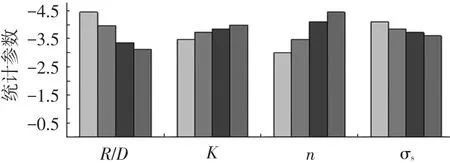
图3 各因素影响趋势分析

4 数值模拟试验

由于应力中性层位移Hσ无法通过物理试验直接测得，通过测量成形质量对Hσ进行间接验证的方法却又无法体现各参数对Hσ的影响规律，因此为确定各参数对Hσ的影响规律，本文采用有限元数值模拟方法对理论分析结果进行验证，该方法不仅可以直观地显示应力中性层的位置，而且能较好地模拟出各参数对Hσ的影响规律．

有限元模型基于ANSYS/LS－DYNA建立，且模型的可靠性已验证［12］，模拟采用各参数设置如下：管材外径D＝25 mm，管材壁厚t＝1 mm，弹性模量E＝169 GPa，密度ρ＝7．83 g/cm3，屈服强度，塑性系数K＝1 200 MPa，泊松比u＝0．28，弯曲角度为90°．弯曲成形后，沿弯曲角度45°处进行剖切，有限元模型及剖切后的横截面如图4所示．

将数值模拟采用的参数代入公式（17），Hσ理论计算值与模拟值的对比结果如图5所示，显然，Hσ随R/D和n的变化趋势相同，验证了理论计算公式的正确性，但由于理论分析时没有考虑压模压力、助推力等工艺参数对应力中性层位移的影响，造成了计算值与有限元模拟值的少量偏差，因此仍需在后续工作中深入研究．

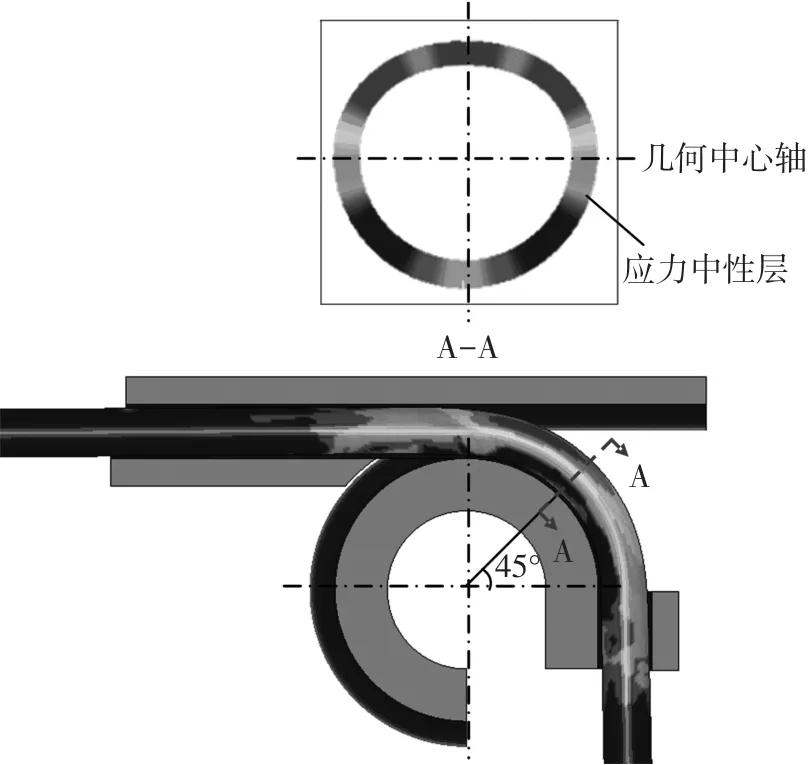
图4 管材弯曲有限元模型及横截面应力分布

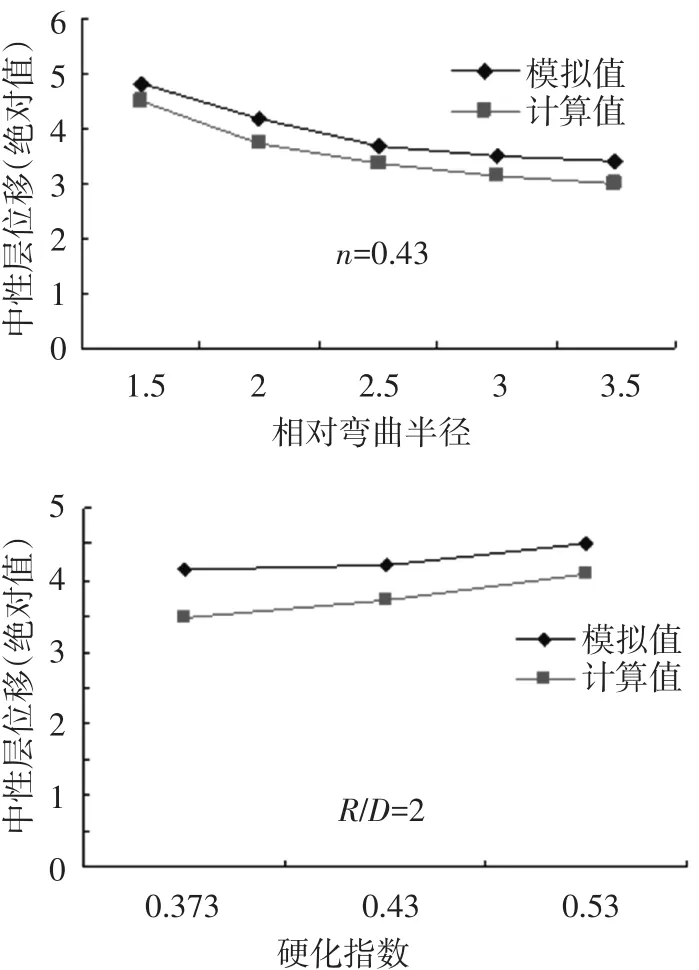
图5 应力中性层位移计算值与数值模拟值对比

5 结 论

1）在平面应力假设条件下，分别建立了弯管内、外侧微元体力学平衡方程，基于塑性力学全量理论，推导出管材的三向应变分布函数，周向分布曲线表明周向应变εα和径向应变εt在数值上大小相当，管材弯曲处于典型的三向应变状态．

2）根据管材弯曲轴力平衡条件，推导了基于R/D和材料性能参数的应力中性层位移Hσ的近似计算公式，由Hσ＜0可知，在管材弯曲过程中，应力中性层向弯曲中心产生了移动．

3）利用正交设计方法对影响Hσ的因素进行了敏感性分析，分析结果表明R/D和n是影响Hσ的最主要因素，其移动距离随R/D的增大而减小，随n值的增大而增大，其它因素影响不显著．

参考文献：

［1］YANG He，LIHeng，ZHANG Zhiyong，et al．Advances and trendson tube bending forming technologies［J］．Chi⁃nese Journal of Aeronautics，25（2012）1－12．

［2］Al⁃QURESHI H A．Elastic⁃plastic analysis of tube bending［J］．International Journal of Machine Tools＆Manufacture，1999（39）：87－104．

［3］鄂大辛，宁汝新，李延民，田鑫．弯管壁厚减薄与材料特性关系的试验研究．材料科学与工艺，2008，16（2）：200－203．E Daxin，NING Ruxin，LIYanmin，TIAN Xin．Experi⁃mental study on the wall thickness thinning of the curved tube affected by material property［J］．Materi⁃als Science＆Technology，2008，16（2）：200－203．

［4］YANG H，LI H，ZHAN M．Friction role in bending behaviors of thin⁃walled tube in rotary⁃draw⁃bending under small bending radii［J］．Journal of Materials Processing Technology，2010（210）：2273－2284．

［5］E Daxin，LIU Yafei．Springback and time⁃dependent springback of 1Cr18Ni9Ti stainless steel tubes under bending［J］．Materials and Design，2010（31）：1256－1261．

［6］姜银方，袁国定，杨继昌，汪建敏．拼焊板弯曲回弹的理论与试验研究［J］．机械工程学报，2005，41（12）：200－203 JIANG Yinfang，YUAN Guoding，YANG Jichang，et al．Springback in the Bending for TailorWelded Blanks in Theory and Experiment［J］．Chinese Journal of Mechanical engineering，2005，41（12）：200－203

［7］官英平，张庆，赵军．中性层内移对弯曲回弹的影响［J］．锻压技术，2007，32（2）：26－29 GUAN Yingping，ZHANG Qing，ZHAO Jun．Influence of neutral layer inside displacement on bending springback［J］．Foreign＆Stamping Technology，2007，32（2）：26－29

［8］TANG N C．Plastic⁃deformation analysis in tube ben⁃ding［J］．International Journal of Pressure Vessels and Piping，2000（77）：751－759．

［9］刘光武，胡勇，王呈方．弯管回弹的理论分析．武汉理工大学学报，2007，29（2）：136－138．LIU Guangwu，HU Yong，WANG Chengfang．Theoritical Analysis on the Spring⁃back of Pipe Bending［J］．Journal of Wuhan University of Technology，2007，29（2）：136－138．

［10］鄂大辛，郭学东，宁汝新．管材弯曲中应变中性层位移的分析．机械工程学报，2009，45（3）：307－310．E Daxin，GUO Xuedong，NING Ruxin．Analysis of Strain Neutral Layer Displacement in Tube⁃bending Process［J］．Journal of Mechanical Engineering，2009，45（3）：307－310．

［11］倪恒，刘佑荣，龙治国．正交设计在滑坡敏感性分析中的应用．岩石力学与工程学报，2002，21（7）：989－992．NIHeng，LIU Yourong，LONG Zhiguo．Applications of orthogonal design to sensitivity analysis of landslide［J］．Chinese Journal of Rock Mechanics and Engineering，2002，21（7）：989－992．

［12］CHENG Pengzhi，TANG Chengtong，ZHAO Shuo，et al．Study on quality forecast and process parameters optimization platform of NC tube bending［C］∥Proceedings of 2010 International Conference on Intelligent Control and Information Processing，ICICIP，2010：701－706．

（编辑 张积宾）

The calculation and influencing factors analysis of stress neutral layer displacement in tube bending

JIA Meihui，TANG Chengtong，LIU Jianhua

（Key Laboratory of Fundamental Science for Advanced Machining，Beijing Institute of Technology，Beijing 100081，China）

To study the displacement and influencing factors of the stress neutral layer in tube bending，the stress⁃strain discipline is analyzed based on the plastic theory．Then the approximate formula of the stress neutral layer displacement is deduced with the consideration of the wall thickness variation and the material hardening characteristics．Finally，to discover the sensitivity factors of the stress neutral layer displacement，the orthogonal designmethod is introduced．It is considered that the relative bending radius and the hardening exponent has significant effects on stress neutral layer displacement，while the other parameters are not obvious．The comparison of theoretical calculations and numerical simulation results prove the correctness and validity of the theoretical analysis．

tube bending；stress neutral layer；orthogonal design；sensitivity analysis

TH386．3

A

1005－0299（2014）02－0112－05

2012－05－14．

“十二五”国防基础科研项目（A2220110008）；国家自然科学基金资助项目（50805009）．

贾美慧（1978－），女，博士生．

贾美慧，E⁃mail：jiameihui2008＠163．com．