基于速度误差的系统级标定方法

徐庆九，孙时珍，戴洪德

（1.海军航空工程学院控制工程系，山东烟台264001；2.海军装备部天津局，北京100086）

基于速度误差的系统级标定方法

徐庆九1，孙时珍2，戴洪德1

（1.海军航空工程学院控制工程系，山东烟台264001；2.海军装备部天津局，北京100086）

为降低捷联惯导系统误差参数标定过程对高精度转台的要求，提出一种基于速度误差的系统级标定方法。在惯性器件误差参数模型和捷联惯导系统误差方程的基础上，以惯导系统转动前后的导航速度误差为观测量，编排设计旋转方案，对加速度计和陀螺的误差参数进行拟合标定。仿真结果表明，与传统的分立式标定方法相比，在保证标定精度的同时，对高精度转台的要求更低，可应用于外场标定。

捷联惯导；误差方程；系统级标定

捷联惯导系统由于其成本低、结构简单、重量轻、可维护性好以及可靠性高等优点[1]，已广泛应用于陆用平台、航海、航空和航天等民用领域和军用领域[2]。陀螺仪和加速度计作为捷联惯导系统的核心部件，其确定性误差是影响系统导航精度的主要误差源。因此，捷联惯导在使用前必须通过标定实验确定惯性仪表的各项误差系数，并在捷联惯导系统中进行补偿[3]。

通常在实验室基于高精度转台所提供的精确姿态和相关转动基准，利用多位置静态测试和速率测试分别对加速度计和陀螺的误差参数进行标定[4-5]。传统的标定过程依赖高精度转台，转台的精度制约着标定结果的精度，以至于制约着高精度捷联惯导系统的发展。

系统级标定方法是将捷联惯导系统的导航误差作为观测量，通过拟合估计的方法对惯性器件的误差参数进行标定。这降低了对高精度转台的要求，适合现场标定。

本文主要对基于导航速度误差的拟合标定方法进行编排设计，从而对惯性器件的误差参数进行标定。

1 惯性器件误差参数模型

1.1坐标系定义

本文选取i系为地心惯性坐标系，e系为地球坐标系，n系为导航坐标系，b系为载体坐标系，a系为加速度计敏感轴坐标系，p系为加速度计标定参数坐标系，g系为陀螺敏感轴坐标系。

1.2 惯性器件误差参数模型

定义加速度计标定参数坐标系p系如下：令其xp轴与加速度的敏感轴xa重合，规定yp轴在xaya平面内，并与xp轴垂直，则xp轴、yp轴与zp轴构成右手直角坐标系[6]。

忽略噪声，加速度计的误差参数模型可写为

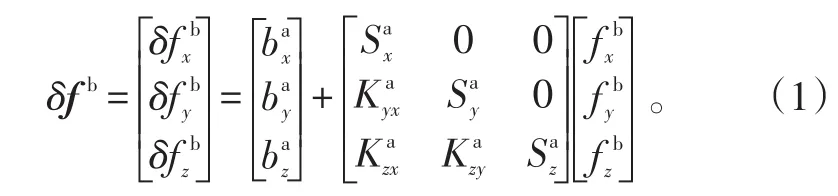
为使加速度计和陀螺的标定参数坐标系相一致，忽略噪声，则陀螺的误差参数模型可以表示为

从式（1）和（2）可以看出，惯性器件的误差参数模型中包括标度因数误差项、安装误差项和零偏误差项共21个误差参数，即实现了加速度计和陀螺的标定参数坐标系相一致，又减少了所需标定误差参数项的个数，使标定过程得到简化[7]。

2 惯导系统误差方程

为计算方便，取北—东—地为导航坐标系，则基于捷联惯导系统的误差模型方程[8-9]，有，

则在静基座条件下，系统误差方程可写为：

式（5）、（6）建立起导航误差和惯性器件误差参数之间的关系，即可通过将导航速度误差作为观测量，进而对加速度计和陀螺的误差参数项进行标定。

3 标定原理及标定编排设计

对所标定惯性器件进行旋转后，导航速度误差主要由惯性器件的误差参数项引起，所以可通过对惯导系统进行位置翻转的编排设计，充分激励出误差参数项以进行标定[10-13]。

设每次旋转初始时间和终止时间分别为t=0和 t′=T，则水平速度误差变化率可以表示为：

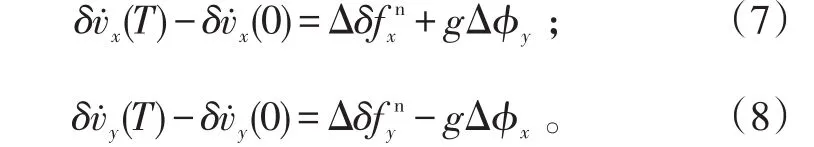
由于地球自转角速度与惯导系统转动角速度相比量级较小，故可将其忽略不计。

另外，对式（5）求导可得：

依据充分激励惯性器件误差参数的原则，编排设计三组旋转标定方案，每组初始位置使x、y、z轴分别指向正北方向，分别转动3次，每次转动角度为π，具体如图1所示。各位置的捷联矩阵和比力测量输入fb如表1所示。

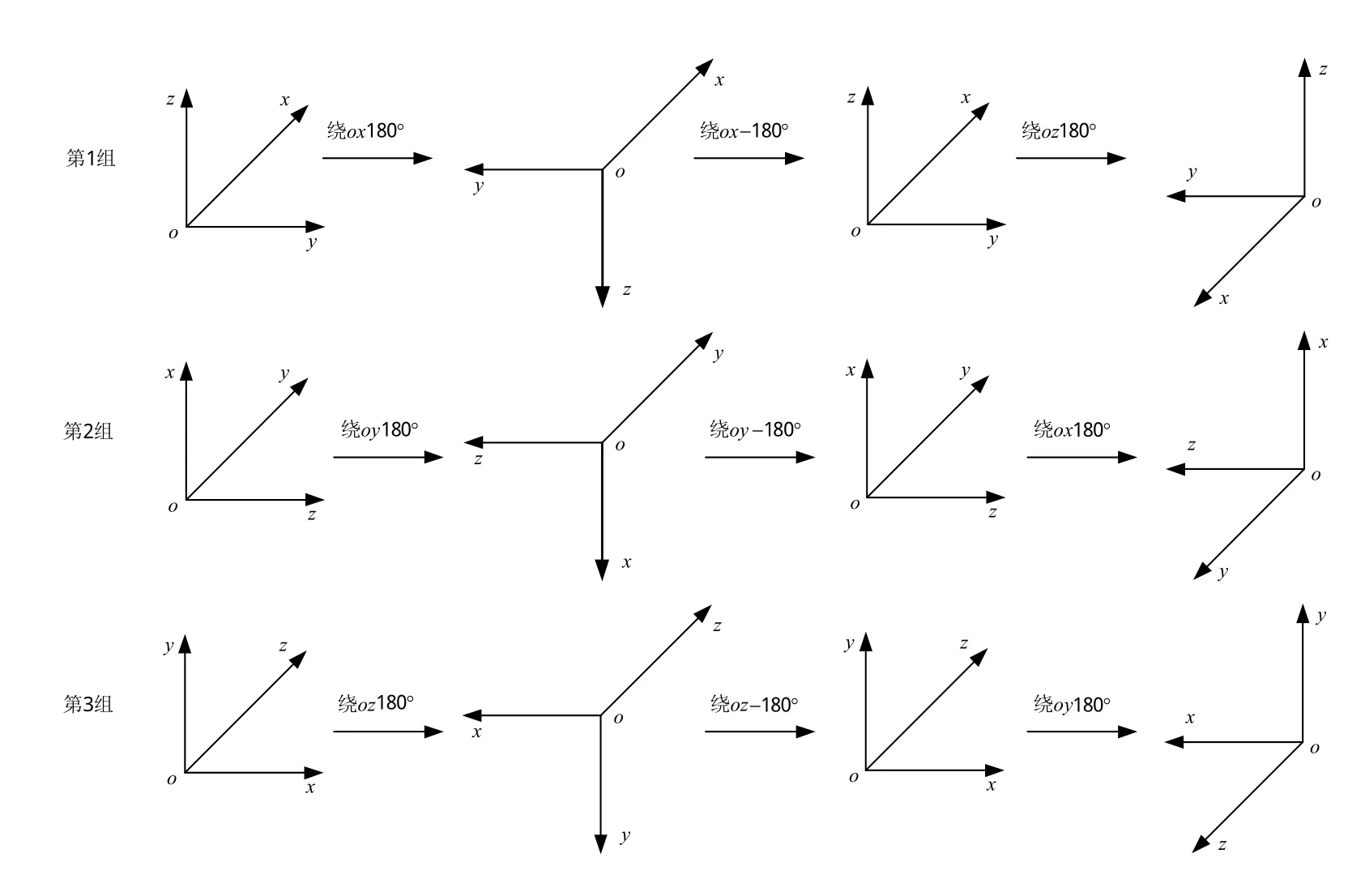
图1 基于速度误差的系统级拟合标定方法旋转示意图Fig.1 Schematic diagram of the systematic fitting calibration method based on speed error

表1 旋转各位置捷联矩阵和比力测量输入Tab.1 Specific force input and strap down matrix of each position

惯导系统在进行标定编排旋转之后，将导航速度误差作为观测量可对加速度计和陀螺的误差参数进行标定。

对于第1组标定编排旋转。

1）第1次旋转后可以得到：

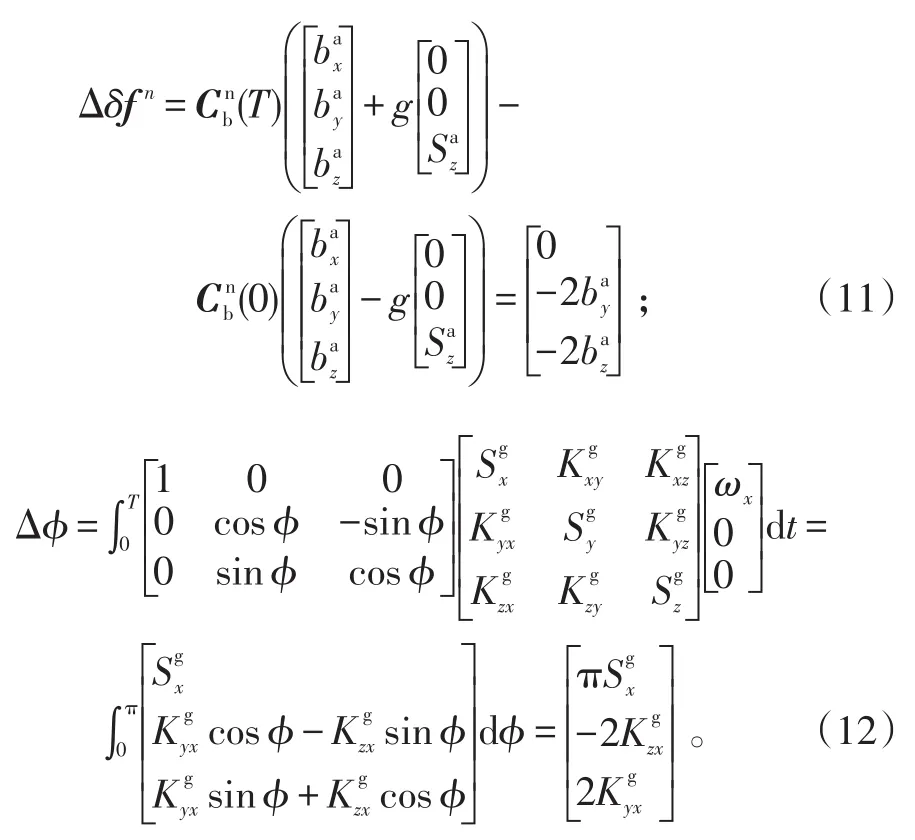
将式（11）和（12）代入式（7）可得

同样对于式（8）可得

2）第2次旋转后可以得到：

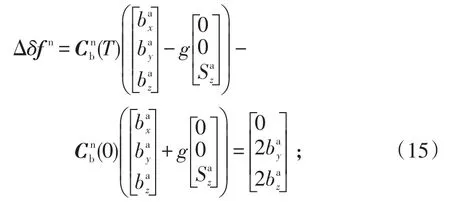
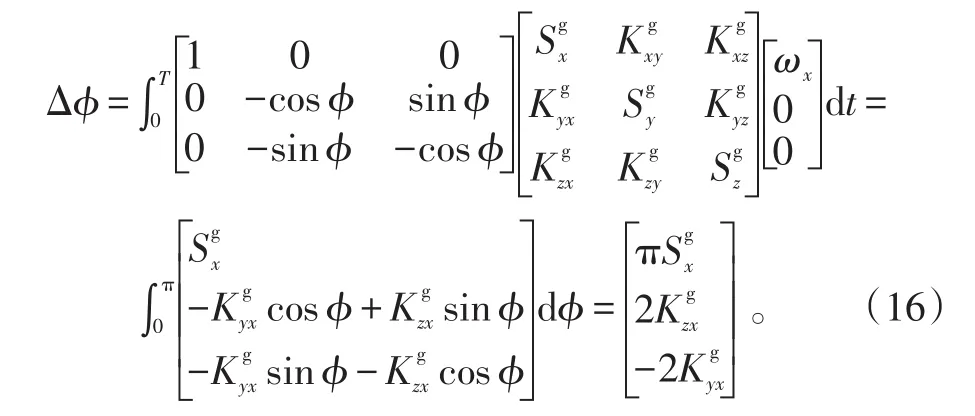
将式（15）和（16）代入式（7）可得

同样对于式（8）可得

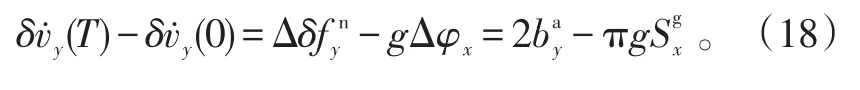
3）第3次旋转后可以得到：

将式（19）和（20）代入式（7）可得

同样对于式（8）可得

而姿态误差也可用速度误差变化率表示，则式（9）和（10）可以表示为：

而从式（5）和（6）可得

对第2组和第3组标定编排旋转，标定过程与第1组相类似，将每组每次旋转分别记为≡δv˙x(T)-δv˙x(0)和≡δv˙y(T)-δv˙y(0)，下标i表示旋转次序，上标j表示标定组数，各组标定误差观测方程如表2所示。

表2 旋转编排各组标定误差观测方程Tab.2 Observation equation of calibration scheme

利用表2中的各组标定误差观测方程，可对惯性器件加速度计和陀螺的误差参数求解如下：

上面只标定出了陀螺的标度因数项、安装误差项和加速度计的零偏误差项、安装误差项。对陀螺的零偏误差项，当每组旋转时利用式（23）、（24）和（28）计算即可，对于加速度计的标度因数项，可分别利用每组首次旋转的天向速度误差求解即可，以第1组为例：

至此标定出加速度计和陀螺的全部误差参数项。

4 仿真结果与标定精度分析

基于以上标定编排设计对陀螺和加速度计各误差参数进行标定，仿真条件设置为：假设当地纬度为北纬38°，惯导系统进行旋转时，转速设为10(°)/s，在静态位置静止1min，转台角位置控制误差和轴正交度误差均设为2"，加速度计和陀螺的测量误差分别为5×10-5g和0.01(°)/h，其仿真标定结果对比见表3、4。

表3 加速度计标定仿真结果对比Tab.3 Contrast of simulation results of accelerometer calibration

表4 陀螺标定仿真结果对比Tab.4 Contrast of simulation results of gyroscope calibration

从表3、4可以看出，与传统的分立式标定方法相比，加速度计的标度因数项和陀螺的零偏误差项的标定精度稍差，是因为对其计算过程中含有速度误差的二次积分项和姿态误差项。总体来说，基于速度误差的系统级拟合标定法对加速度计和陀螺的误差参数标定结果优于传统分立式标定法的标定结果。

5 结论

本章主要研究了基于速度误差的系统级拟合标定方法，以导航速度误差为观测量，编排设计了3组旋转方案，建立了相应的标定观测方程以对惯性器件的误差参数进行标定。仿真结果表明，系统级标定法在保证标定精度的同时，降低了对高精度转台的要求，效果较好。

[1]袁保伦.四频激光陀螺旋转式惯导系统研究[D].长沙：国防科学技术大学，2007：3-5. YUAN BAOLUN.Research on rotating inertial navigation system with four-frequency differential laser gyroscope[D].Changsha：National University of Defense Technology，2007：3-5.（in Chinese）

[2]张开东.激光陀螺捷联惯导系统连续自动标定技术研究[D].长沙：国防科学技术大学，2002：3-4. ZHANG KAIDONG.Research on the technology about self calibration of laser gyroscope based strapdown inertial navigation system[D].Changsha：National University of Defense Technology，2002：3-4.（in Chinese）

[3]CUREY R K，ASH M E，THIELMAN L O，et al.Proposed IEEE inertial systems terminology standard and other inertial sensor standards[C]//IEEE Position Location and Navigation Symposium.Monterey，California：IEEE，2004：83-90.

[4]TITTERTON D H，WESTON J L.Strapdown inertial navigation technology[M].London：Peter Peregrinus Ltd.on behalf of the Institute of Electrical Engineers，2004：253-255.

[5]ZHANG H，WU Y，WU W.Improved multi-position calibration for inertial measurement units[J].Measurement Science and Technology，2010，21（1）：1-11.

[6]SKOG I，HANDEL P.Calibration of a MEMS inertial measurement unit[C]//XVII IMEKO World Congress，Metrology for a Sustainable Development.Rio de Janeiro，Brazil，2006：326-329.

[7]谢波，秦永元，万彦辉.激光陀螺捷联惯导系统多位置标定方法[J].中国惯性技术学报，2011，19（2）：157-162. XIE BO，QIN YONGYUAN，WAN YANHUI.Multiposition calibration method of laser gyro SINS[J].Journal of Chinese Inertial Technology，2011，19（2）：157-162.（in Chinese）

[8]肖桂平.光学陀螺捷联惯导系统的标定精度分析[D].长沙：国防科学技术大学，2008：8-11. XIAO GUIPING.Accurancy of optic gyro strapdown inertial navigation system calibration[D].Changsha：National University of Defense Technology，2008：8-11.（in Chinese）

[9]张红良.陆用高精度激光陀螺捷联惯导系统误差参数估计方法研究[D].长沙：国防科学技术大学，2010：24-26.

ZHANG HONGLIANG.Research on error parameter estimation of land high precision ring laser gyroscope strapdown inertial navigation system[D].Changsha：National University of Defense Technology，2010：24-26.（in Chinese）

[10]KAO W W，TSAI C L.Adaptive and learning calibration of magnetic compass[J].Measurement Science and Technology，2006，17（11）：3073-3082.

[11]JURMAN D，JANKOVEC M，KAMNIK R，et al.Calibra

tion and data fusion solution for the miniature attitude and heading reference system[J].Sensors and Actuators A：Physical，2007，138（2）：411-420.

[12]MIRZAEI F M，ROUMELIOTIS S I.A Kalman filterbased algorithm for IMU-camera calibration：Observability Analysis and Performance Evaluation[J].Robotics，IEEE Transactions on，2008，24（5）：1143-1156.

[13]BONNET S，BASSOMPIERRE C，GODIN C，et al.Calibration methods for inertial and magnetic sensors[J].Sensors andActuatorsA：Physical，2009，156（2）：302-311.

Abstrat:In order to reduce the demand of precise turntable in the calibration of error parameters in strapdown inertial navigation system,a systematic calibration method based on velocity error was proposed.Based on the model of inertial sensors and error equation of SINS,the velocity errors of inertial navigation system before and after rotation were used as observational vectors.Then the rotation scheme was designed to calibrate the error parameters of inertial sensors.The simulation results showed that,compared with the traditional calibration method,systematic calibration method has lower demand of precise turntable which can be applied to the field calibration while maintaining the calibration accuracy.

Systematic Calibration Method Based on Velocity Error

XU Qing-jiu1,SUN Shi-zhen2,DAI Hong-de1
（1.Department of Control Engineering,NAAU,Yantai Shandong 264001,China; 2.Tianjin Bureau of NED,Beijing 100086,China）

SINS;error equation;systematic calibration

V249.32+2

A

1673-1522（2014）01-0009-05

10.7682/j.issn.1673-1522.2014.01.003

2013-09-04；

2013-11-25

徐庆九（1969-），男，副教授，硕士。