用于雷达方位超分辨的约束迭代Tikhonov正则化算法

邹建武，贾兴亮，高明哲，董巍

（1.海军航空工程学院研究生管理大队，山东烟台264001；2.海军装备部西安局，兰州730070；3.海军司令部航空兵部，北京100071）

用于雷达方位超分辨的约束迭代Tikhonov正则化算法

邹建武1，贾兴亮2，高明哲1，董巍3

（1.海军航空工程学院研究生管理大队，山东烟台264001；2.海军装备部西安局，兰州730070；3.海军司令部航空兵部，北京100071）

针对Tikhonov正则化算法噪声适应能力差和不便于引进额外的约束对解进行限制等缺点，利用迭代Tikhonov正则化算法对雷达方位超分辨进行研究，证明了迭代Tikhonov正则化反卷积公式的收敛性，分析了迭代Tikhonov正则化算法的频域性质，在存在噪声的情况下，提出相应的噪声抑制方法，得到约束迭代Tikhonov正则化算法。针对不同信噪比情况进行了计算机仿真实验，结果表明，与迭代Tikhonov正则化算法相比，约束迭代Tikhonov正则化算法具有较强的噪声适应能力，与常用的约束迭代方法（CID）算法相比，具有较快的收敛速度，初步验证了算法的有效性。

超分辨；迭代Tikhonov正则化；迭代算法；反卷积

雷达方位超分辨就是在不改变雷达工作体制前提下，利用数字信号处理技术分辨同一雷达波束内的几个等距目标。一直以来，雷达的方位分辨力受限于发射波的频率和天线孔径大小，因而寻找改善方位分辨力的新方法尤为迫切。国内外学者对此问题展开了广泛深入的研究，主要的方位超分辨方法有：迭代反卷积法、Richardson-Lucy算法、广义逆滤波法和维纳逆滤波算法等[1-9]。

文献[1]提出了一种约束迭代方法（CID）和一种快速迭代算法（FCID），在特定情况下，方位分辨力改善了4倍。刘瑞冬等[2]分析并仿真对比了CID算法和FCID算法的超分辨性能，提出了FCID-CID算法，该算法既减小了算法的运算量，又能抑制噪声伪峰，并且放宽了FCID迭代次数的估计要求。Jinchen Guan等[3]利用基于最大后验概率准则的迭代算法对方位超分辨进行研究，在20dB的情况下，分辨力可提高5.3倍；文献[4-5]利用基于Bayesian准则的R-L算法实现了雷达方位超分辨，并对算法的超分辨性能进行了深入研究，该算法在信噪比0dB条件下，方位分辨力提高2倍，但是上述2种方法均是基于噪声分布为泊松分布的情况下。丁义元等[6]提出利用广义逆滤波方法提高实孔径雷达角分辨力，在低信噪比的条件下，有效地改善了实孔径雷达的角分辨力，但时域计算较为复杂。文献[7-9]利用维纳逆滤波算法对提高雷达方位角分辨力进行了研究，在雷达回波信噪比大于30dB的情况下，该方法可实现方位超分辨，证明了维纳逆滤波算法实现方位超分辨是可行的，但不适用于低信噪比条件。

本文首先建立雷达目标的方位回波模型，针对Tikhonov正则化的缺点，利用迭代Tikhonov正则化算法对方位超分辨进行研究，证明迭代公式的收敛性；分析算法的频域性质，针对噪声对迭代算法的影响，给出迭代约束条件，以保证在雷达数据存在噪声的条件下，得到目标方位的理想近似解；最后，利用此算法进行计算机仿真。结果表明，此约束迭代算法能在低信噪比条件下，具有区分相距半功率波束宽度内的目标的能力，与常用的约束迭代方法（CID）算法相比，具有较快的收敛速度。

1 雷达方位回波信号模型与反卷积的频域解

此处忽略俯仰角，仅考虑方位角的变化。假设常规雷达在方位向上扫描，实孔径雷达的方位回波信号表现为天线方向图与目标方位信息卷积。在非相参雷达系统中，只考虑雷达方位回波功率值。为方便讨论，雷达目标方位回波模型可以表示为

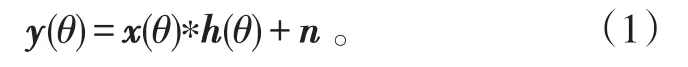
将式（1）转换为矩阵—向量表达式：

y=H1x+n。（2）

式（2）中：

y=[y(1)y(2)…y(N+M-1)]T=y(θ)T；（3）

x=[x(1)x(2)…x(N)]T=x(θ)T；（4）

h(θ)=[h(1)h(2)…h(M)]（5）

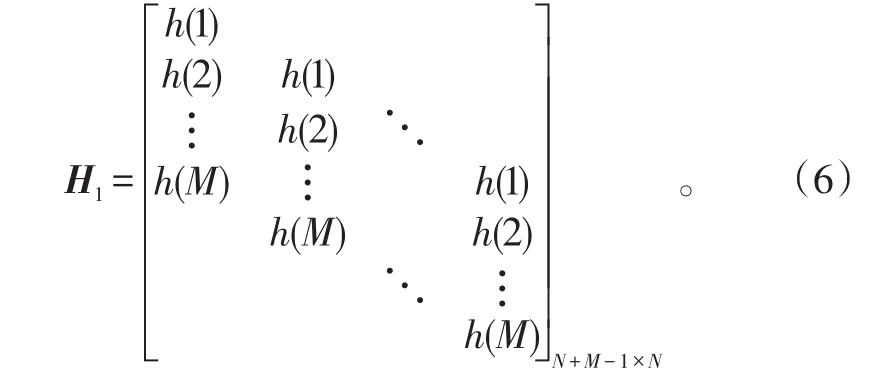
对（1）做傅里叶变换可得

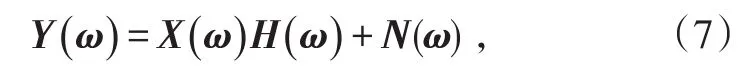
加性噪声主要是接收机噪声，本文主要考虑加性噪声。加性噪声在接收机通带内均可视为白噪声。

鉴于天线系统的低通效应，目标方位信息的高频成分被抑制或者丢失。在反卷积恢复信号高频信息的过程中，由于会趋于无穷大，使噪声的频谱信息放大，导致X˜() ω误差过大，使得反卷积问题呈现病态，利用Tikhonov正则化算法法能缓解此病态性。此处，把X˜()

ω或者其逆傅里叶变换形式称为病态解。

2 约束迭代Tikhonov正则化算法

2.1 迭代Tikhonov正则化算法

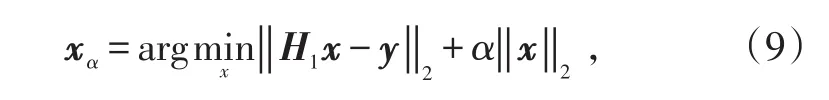
式中，α＞0为正则化参数。

当α选择恰当时，极小值点xα可以作为真实解的理想近似值[10]。

由文献[10]可知，求解式（9）极小化问题等价于求解如下线性方程组：式（10）中：I为单位矩阵。正则化参数α对雷达超分辨问题的求解起着关键作用，当α取得过小时，求取的解依然存在不稳定的性质；当α取得过大时，求取的稳定解过分光滑，又与真实解相差过大。因此，α的选取应该兼顾这2种情况。α值得选取主要有先验和后验2类策略。

由于Tikhonov正则化算法噪声适应能力差和不便于引进额外的约束对解进行限制等缺点，我们利用Tikohonov迭代正则化方法对上述问题进行求解，其频域迭代形式如下：

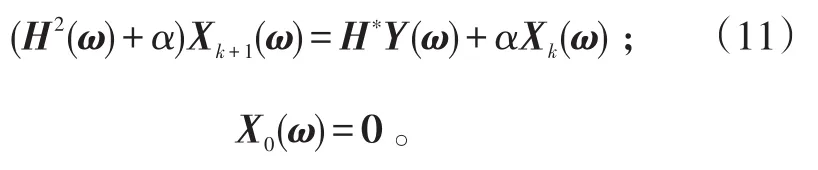
当k=1时，此算法变为Tikhonov正则化方法，针对式（11）可知，和是一组向量，由于α为一个正常数中的分量也是一个正数，所以，

于某一X。

2.2 迭代算法的频域分析及噪声影响分析

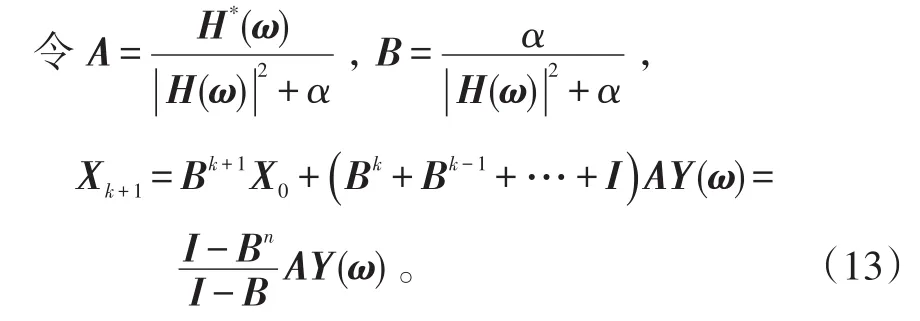
此处为简化分析，假设雷达天线方向图是高斯型，且H(ω)=e-ω2（1/H(ω)称为逆滤波），将其代入上式即可得到迭代Tikhonov正则化算子

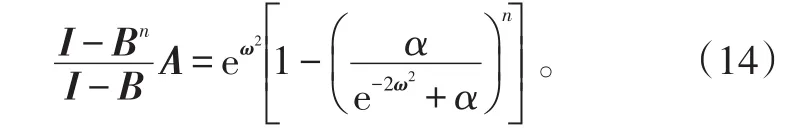
此算子随着参数α和迭代次数n的变化如图1和图2所示。由图1、2可知，正则化参数α的取值对其频率响应影响较大，此处α值选取过大，则每一步求取的解过于光滑；α值选取过小时，求取的解受到噪声的较大影响，同而α值的选取受到天线方向图函数的影响，因而要综合考虑α的取值。迭代Tikhonov正则化算子具有压制高频信息，放大低、中频信息的能力，但此时迭代Tikhonov正则化算子的分辨能力依然有限；随着迭代次数n的增大，其高频放大能力得到增强，迭代Tikhonov正则化算子的分辨能力变差。由于上述原因，在噪声存在的情况下，利用迭代Tik-honov正则化算法求解时，低、中频段的噪声被放大，迭代解随n的增大收敛于式（8）的病态解，而使得迭代Tikhonov算法不能分辨目标。因此，在应用该算法时，要考虑应用相关的消除噪声或抑制噪声技术，对迭代过程中的解进行约束，使其收敛于理想近似解。

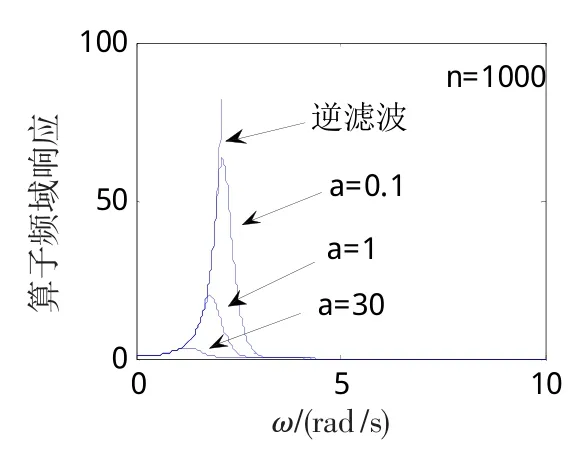
图1 迭代Tikhonov正则化算子频域响应曲线（n=1 000）Fig.1 Iteration Tikhonov regularization operator frequency response curve（n=1 000）

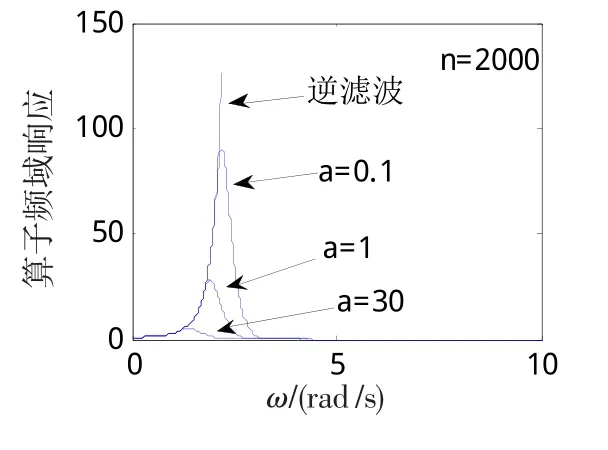
图2 迭代Tikhonov正则化算子频域响应曲线（n=2 000）Fig.2 Iteration Tikhonov regularization operator frequency response curve（n=1 000）

2.3 约束迭代Tikhonov正则化算法

为抑制噪声，在此处给出2种约束条件：正性约束条件和有界约束条件。实际雷达接收机处获得实孔径雷达回波信号是功率信息，具有非负性，因而在迭代计算中，回波信号满足正性约束，定义P为正性算子[12]：

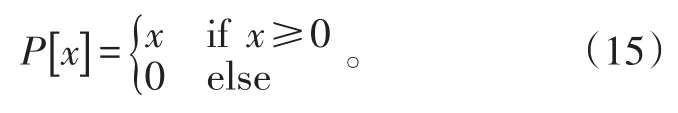
雷达波束扫描范围内的目标的范围是有界的，经过波束扫描后得到的回波信号也是有界的；定义T为有界约束算子[12]：

将式（15）与式（16）代入式（11）可得

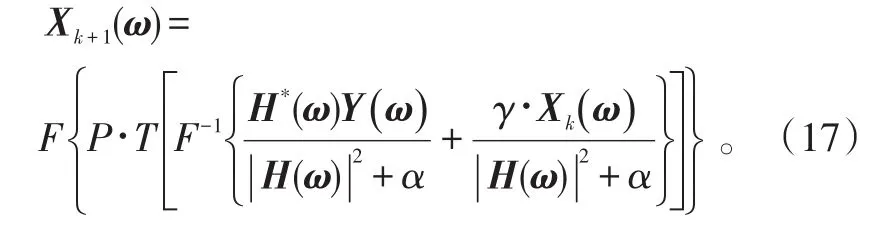
2.4 迭代终止条件

通常，很难确定用迭代算法得到的超分辨效果，本文提出利用误差标准作为算法终止迭代条件，在有噪声存在和迭代算法加上初值和约束条件的情况下，基于方位分辨结果趋于稳定解的考虑，利用相邻迭代次数得到的超分辨结果之间的误差来判断迭代是否终止。

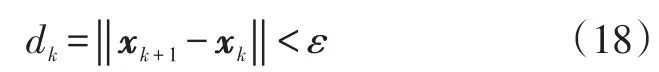
式中：ε为误差标准，此时的xk+1是式（17）中Xk+1(ω)的时域表现形式，因而，式（17）要得到具体的解析公式很困难。

当dk＜ε时，迭代终止。迭代次数为k+1次；当dk≥ε时，继续迭代。

3 计算机仿真结果

假设脉冲重复频率为1 000Hz，扫描速度为100(°)/s，扫描范围为-15°～15°，天线方向图采用高斯模型，半功率波束宽度为4°，误差标准ε=1×10-6；根据所采用的天线方向图函数和经验，取α=50；利用约束迭代Tikhonov正则化算法，在信噪比分别为0dB、10dB、20dB、30dB情况下，对间隔1/2半功率波束宽度的2个点目标（分别位于-1°和1°）进行了分辨，仿真结果如图3~10所示。

图3 信噪比0dB的目标方位回波Fig.3 Target azimuthechoofSNR 0dB

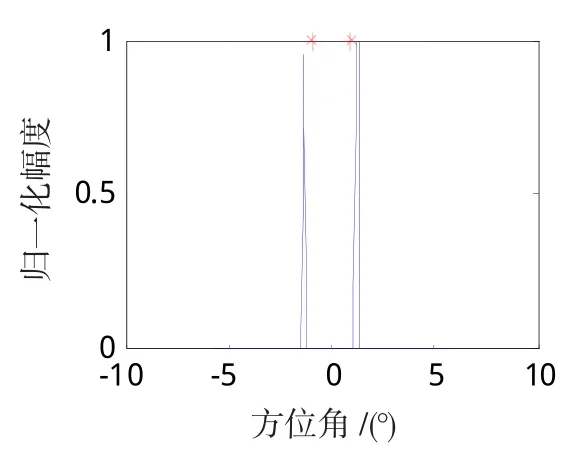
图4 信噪比0dB反卷积结果Fig.4 DeconvolutionresultsofSNR 0dB

图5 信噪比10dB的目标方位回波Fig.5 Target azimuthechoofSNR 10dB

图6 信噪比10dB的反卷积结果Fig.6 Deconvolution results ofSNR 10dB

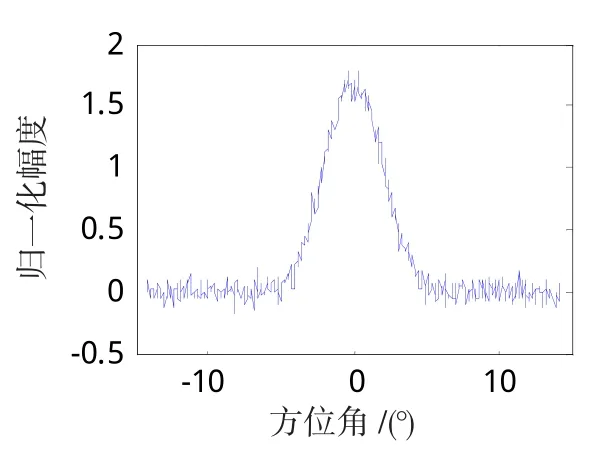
图7 信噪比20dB的目标方位回波Fig.7 Target azimuth echo ofSNR 20dB

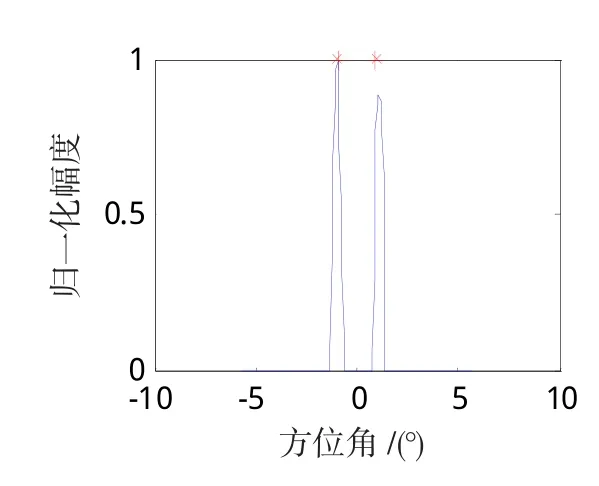
图8 信噪比20dB的反卷积结果Fig.8 Deconvolution results ofSNR 20dB

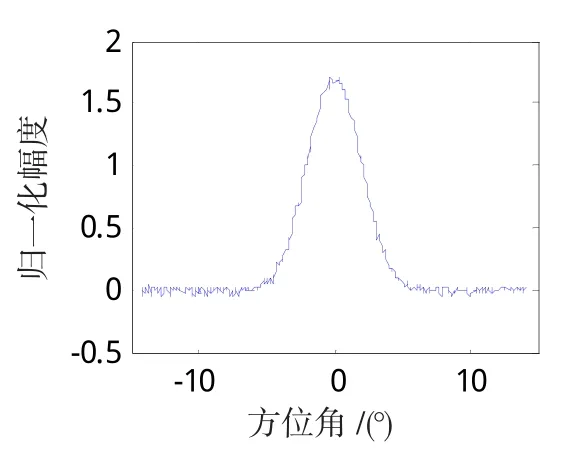
图9 信噪比30dB的目标方位回波Fig.9 Target azimuth echo ofSNR 30dB

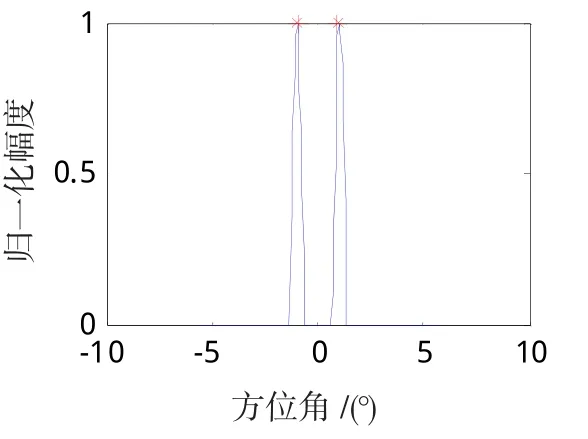
图10 信噪比30dB的反卷积结果Fig.10 Deconvolution results ofSNR 30dB

由图3~10可知，在误差标准下，经过有效次迭代，约束迭代Tikhonov算法在高信噪比条件下分辨能力良好，随着信噪比降低，虽然也能分辨目标，但是分辨精度变差，甚至有时会出现虚假目标，这是由于噪声的随机性过大所导致的。在仿真时，用此方法没有出现所谓的“半收敛”现象（迭代早期阶段，迭代解得到改进，超过一定迭代次数，迭代解趋于发散）。为进一步分析约束迭代Tikhonov正则化算法的性能，利用迭代Tikhonov正则化算法和CID算法与本文算法进行比较。在同样仿真参数、不同信噪比条件下，利用迭代Tikhonov正则化算法（算法1）、CID算法（算法2）和本文算法所能提高的最大分辨倍数见表1。

在同样的仿真参数下，分别用3种算法对不同信噪比条件下的2个点目标进行分辨。由表1可知，3者随信噪比的提高分辨能力改善；迭代Tikhonov正则化算法适用于信噪比较高的条件，在信噪比低于20dB时，失去分辨能力；而约束迭代Tikhonov正则化算法和CID算法适用信噪比较低的情况，约束迭代Tikhonov正则化算法和CID算法同属于迭代反卷积算法，表达式也类似，虽约束迭代Tikhonov正则化算法在分辨能力上与CID算法稍差一点，但在收敛速度上占优势，2种算法在30 dB情况下分辨相隔1/2半功率波束宽度的2点目标时，均方误差与迭代次数的关系对比线见图11。由图11可知，CID算法需较多的迭代次数才能使误差达到约束迭代Tikhonov算法的相同程度。综上所述，初步验证了本算法的有效性。

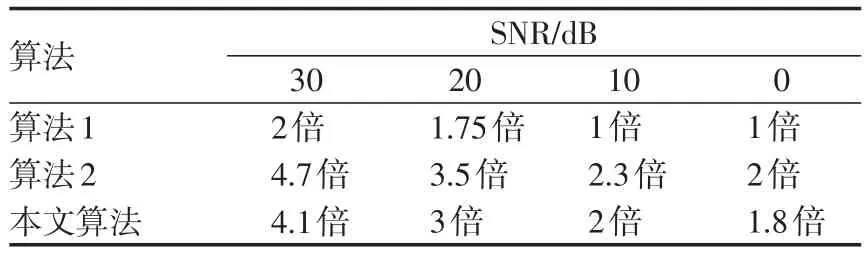
表1 3种算法的分辨性能Tab.1 Resolution performance of three algorithms

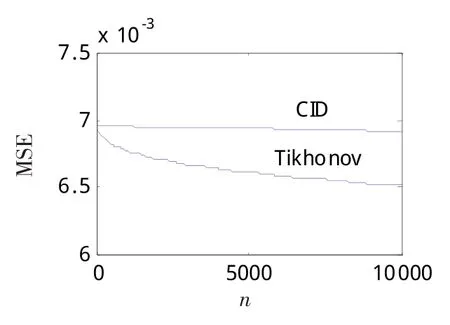
图11 均方误差与迭代次数的关系曲线Fig.11 Curve of the iteration number and MSE

4 结束语

本文针对Tikhonov正则化算法的缺点，利用迭代Tikhonov正则化算法对雷达方位超分辨进行了研究。为了使算法能够收敛到理想近似解，对算法赋予合适的约束条件。仿真表明：在迭代Tikhonov正则化算法不能分辨目标的低信噪比条件下，所提新算法能实现雷达目标方位分辨问题，且收敛速度优于CID算法，初步验证了约束迭代Tikhonov正则化算法的有效性。目前主要不足在于有关α的取值还尚待进一步研究。

[1]MARK A RICHARDS.Iterative noncoherent angular superresolution[C]//IEEENationalRadarConference. 1988：100-105.

[2]刘瑞冬，尚社，张洪太，等.限制迭代去卷积超分辨算法性能研究[J].空间电子技术，2010（2）：63-66. LIU RUIDONG，SHANG SHE，ZHANG HONGTAI，et al.Superresolution agorithm characteristic research of constrained iterative deconvolution[J].Space Electronic Technology，2010（2）：63-66.（in Chinese）

[3]GUAN JINCHEN，HUANG YULIN，YANG JIANYU，et al.Improving angular resolution based on maximum a posteriori criterion for scanning radar[C]//IEEE Radar Conference.2012：451-454.

[4]李惠.实孔径雷达波束锐化算法研究[D].成都：电子科技大学，2010：20-32. LI HUI.Research on beam sharpening algorithm of real aperture radar[D].Chengdu：University of Electronic Science and Technology of China，2010：20-32.（in Chinese）

[5]LI DONGGE，HUANG YULIN，YANG JIANYU.Real beam imaging based on adaptive lucy-richardson algorithm[C]//IEEE Radar Conference.2011：14-17.

[6]丁义元，杨建宇，张卫华，等.改进实孔径雷达角分辨力的广义逆滤波方法[J].电子学报，1993，21（9）：15-19. DING YIYUAN，YANG JIANYU，ZHANG WEIHUA，et al.Improvement of angular resolution of real aperture radar via generalized inverse filtering[J].Acta Electronica Sinica，1993，21（9）：15-19.（in Chinese）

[7]单荣光，李士国，朱力.去卷积实现雷达方位超分辨[J].现代雷达，1993（6）：25-32. SHAN RONGGUANG，LI SHIGUO，ZHU LI.Radar azimuth super-resolution using deconvolution[J].Modern Radar，1993（6）：25-32.（in Chinese）

[8]ZHAO KANG，WANG JIANGUO.Improved wiener filter superresolution algorithm for passive millimeter wave imaging[C]//IEEE Radar Conference.2011：1768-1771.

[9]高明哲，祝明波.噪声对维纳滤波反卷积算法性能影响的分析[J].舰船电子工程，2012，32（12）：35-37. GAO MINGZHE，ZHU MINGBO.Analysis on Noise's Impact on the Performance of Wiener Filter Deconvolution Algorithm[J].Ship Electronic Engineering，2012，32（12）：35-37.（in Chinese）

[10]王彦飞.反演问题的计算方法及其应用[M].北京：高等教育出版社，2007：37-38 WANG YANFEI.Computational methods for inverse problems and their applications[M].Beijing：Higher Education press，2007：37-38.（in Chinese）

[11]徐翠薇，孙绳武.计算方法引论[M].北京：高等教育出版社，2001：154-155. XU CUIWEI，SUN SHENWU.Calculation method introduction[M].Beijing：Higher Education press，2001：154-155.（in Chinese）

[12]SCHAFER R W，MERSEREAU R M，RICHAREDS M A.Constrained iterative restoration algorithms[C]//Proceeding of the IEEE.1981：432-450.

Constrained Iterative Tikhonov Regularization Algorithm for Radar Azimuth Super Resolutionn

ZOU Jian-wu1,JIA Xing-liang2,GAO Ming-zhe1,DONG Wei3
（1.Graduate Students'Brigade,NAAU,Yantai Shandong 264001,China;2.Xi'an Bureau of Naval Equipment Department, Lanzhou 730070,China;3.Aviation Department of Navy Headquaters,Beijing 100071,China）

An iterative Tikhonov regularization algorithm was used based on Tikhonov regularization algorithm,because of its poor noise adoptive ability and without introduction of additional constraints on the solutions.The convergence of the deconvolution formula was proved,the frequency domain characteristics was analyzed,the corresponding noise suppression methods was given,and the constrained iterative Tikhonov regularization algorithm was got.According to the different signal-to-noise ratio（SNR）,the computer simulation experiment was made.The result showed that,compared with iterative Tikhonov regularization algorithm,it had a strong noise adoptive ability,and it had a faster convergence speed,which verified the algorithm efficiency preliminarily.

super resolution;iterative Tikhonov regularization;iterative algorithm;deconvolution

TN959

A

1673-1522（2014）01-0033-05

10.7682/j.issn.1673-1522.2014.01.008

2013-07-17；

2013-12-10

“泰山学者”建设工程专项经费资助项目

邹建武（1986-），男，博士生。