机翼前缘后掠角对飞机RCS影响的数值模拟

徐鸣，左君伟，岳奎志，郁大照

（1.海军装备部，北京100071；2.海军航空工程学院飞行器工程系，山东烟台264001）

机翼前缘后掠角对飞机RCS影响的数值模拟

徐鸣1，左君伟1，岳奎志2，郁大照2

（1.海军装备部，北京100071；2.海军航空工程学院飞行器工程系，山东烟台264001）

为了在飞机总体设计时改善其隐身性能，对机翼前缘后掠角参数化可调的飞机三维数字样机的RCS特性进行了研究。使用CATIA软件，建立机翼前缘后掠角参数化可调的飞机三维数字样机；基于物理光学法和等效电磁流法，采用RCSAnsys软件，使用X波段雷达对飞机进行探测，雷达入射波的俯仰角在-15°、0°和15°条件下，数值模拟机翼前缘后掠角在-30°～+60°之间变化时飞机的RCS特性，并对数值模拟结果进行数理统计分析。在机翼前缘后掠角变化的条件下，飞机RCS特性数值模拟结果表明：飞机头向RCS峰值之一的方位角与机翼前缘后掠角的角度相等；飞机头向RCS算术平均值特性为直机翼大、前掠翼和后掠翼小、大后掠翼更小；飞机侧向和尾向的RCS算术平均值变化相对不大。

飞机总体设计；前缘后掠角；隐身；物理光学法；数值模拟

隐身飞机是现代作战飞机发展的重要方向之一，各军事强国纷纷对隐身飞机进行论证、设计、生产、装备和使用。美国研制的隐身飞机有F-22[1]、F-35[2]、X-45A、X-47B[3]和B-2等，它们已成为或即将成为美国空军和海军作战飞机大家族中尖端的力量。俄罗斯也在研究Su-47、MiG-1.44和T-50[4]等具有隐身特性的作战飞机，它们很有可能成为俄国空军未来的主战力量。我国航空工业部门也在奋起直追，研制隐身作战飞机，已取得相当可观的阶段成果[5]。

国内外专家学者对隐身飞机的设计研究工作已进行了许多年，取得颇丰的研究成果。学者们对隐身飞机进行了机头、机身、机翼、进气道等电磁波强散射部位的隐身外形研究，对隐身材料进行分析，并对雷达隐身、红外隐身、可见光隐身和声隐身等关键技术进行探索，还进行气动、隐身、结构等多学科优化算法研究等等。还有一些文献研究RCS模型与算法，如：文献[6]研究了阻力最小时飞机的配置与隐身的关系；文献[7]研究高斯光束对雷达散射截面的导电圆柱分布的影响；文献[8]基于不同目标的雷达截面散射特征，建立了综合隐身性能分析方法，进行隐形飞机的评估；文献[9]基于鲁棒进化算法研究了无人机的气动和隐身性能；文献[10]研究了对于复杂目标主要散射源识别的集成计算技术，适合解决大型复杂目标和具有较低RCS精度要求的目标；孙聪在文献[11]中总结了F/A-22和F-35等隐身战斗机特点，提出减小天线孔径外形尺寸、缩减天线孔径特征信号、采用低截获概率技术等概念性解决方案；文献[12]研究了飞机表面红外辐射模型，并对红外特征进行了分析，总结了红外隐身缩减策略；文献[13]提出了混合角分裂算法，加速预测大而复杂的目标模型RCS值。国内外专家学者对飞机隐身问题的一系列研究已经很深入，但是对飞机隐身问题的研究还有一些不到位的地方，还未发现关于飞机机翼前缘后掠角对飞机隐身特性影响的研究报道。

F-22的机翼前缘后掠角χ为42°，F-35的χ为33°，B-2的χ为33°，X-45A的χ为43°，X-47A的χ为55°，Su-47的χ为-20°，等等。这些飞机的机翼前缘后掠角与飞机隐身特性有着怎样的定性联系和定量联系，以往学者研究还不到位。本文针对以往专家关于机翼前缘后掠角对飞机隐身特性研究不足的问题，建立机翼参数化可调的飞机三维数字模型，使用物理光学法和等效电磁流法，进行了数值模拟研究，得出RCS特性的分析报告，期望对隐身飞机的设计研究工作提供参考依据。

1 理论基础

机翼前缘后掠角对飞机RCS影响研究的理论依据包括：χ变化时飞机机翼参数化约束模型和RCS测试方法。

1.1 χ变化时飞机机翼参数化约束模型

本文对正常式布局作战飞机的机翼进行参数化约束，并推出χ变化时机翼参数化约束模型，其示意图见图1。

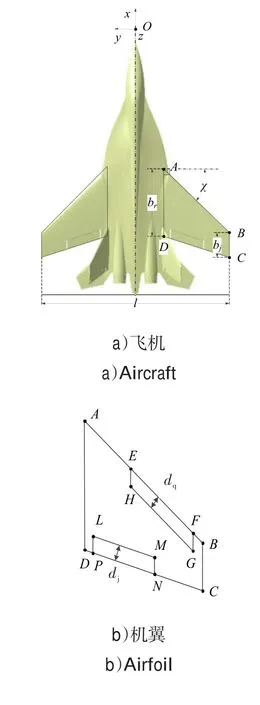
图1 机翼参数化约束示意图Fig.1 Schematic diagram of the airfoil parametric constraints

在图1a）、b）中，χ变化时三维机翼参数化模型说明如下：机翼扭转角为0°，机翼下反角为3°，Oxyz为机翼坐标系；在机翼坐标系下，(xA,yA,zA)为点A坐标，(xB,yB,zB)为点B坐标，…，(xP,yP,zP)为点P坐标；在机翼坐标系下zA=zB=…=zP=0；A、B、C和D点围绕的几何图形为机翼部分，E、F、G和H点围绕的几何图形为前缘襟翼部分，L、M、N和P点围绕的几何形状为襟副翼部分；br为翼身融合体弦长，bj为翼尖弦长，l为翼展；χ为机翼前缘后掠角，规定机翼向后掠为正值，机翼向前掠为负值；机翼翼型在Profili软件中选择AG-10翼型。

机翼约束条件如下：A点和D点位置恒定不变，lAD=br，yA=yD，AD//Oxz；B点和C点位置随χ变化，lBC=bj，yB=yC=-l/2，BC//Oxz；

xB=xA-0.5·l·tanχ；（1）

xC=xB-dj。（2）

式中：lAD为AD间距离（下同）。

前缘襟翼约束条件如下：EF//HG//AB，EH// FG//AD，lEHcosχ=dq为EF和HG间距离，yE=yH为常数，yF=yG为常数。

xE=xA-|yE-yA|·tanχ；（3）

xF=xA-|yF-yA|·tanχ；（4）

xH=xE-dq/cosχ；（5）

xG=xF-dq/cosχ。（6）

襟副翼约束条件如下：LM//PN//DC，LP// MN//AD，dj为LM和PN间距离，yL=yP为常数，yM=yN为常数。

xP=xD-2|yP-yD|·|xC-xD|/l；（7）

xN=xD-2|yN-yD|·|xC-xD|/l；（8）

xL=xP+dj/cos(arctg(2|xC-xD|/l))；（9）

xM=xN+dj/cos(arctg(2|xC-xD|/l))。（10）

1.2 RCS测试方法

本文采用物理光学法计算面元散射和等效电磁流法计算边缘绕射的综合数值模拟作战飞机的RCS特性。

物理光学法计算面元散射的式子如下：

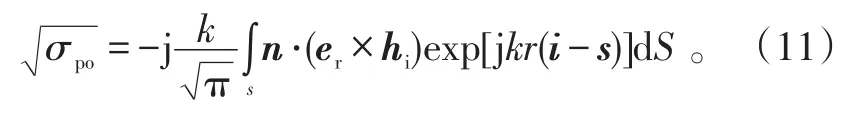
等效电磁流法计算边缘绕射的式子如下：

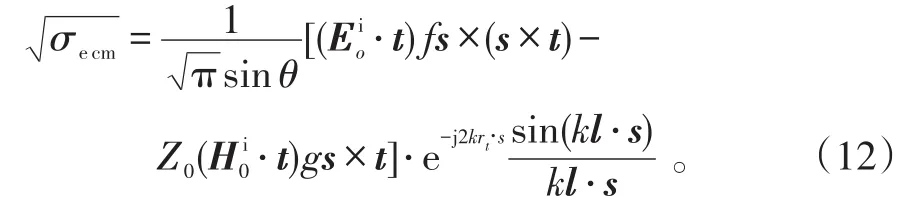
作战飞机的RCS叠加式子如下：

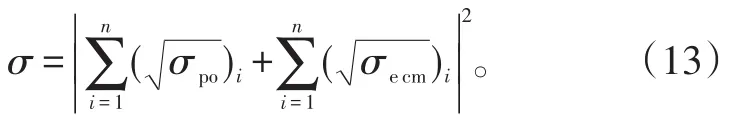
RCS数理统计与单位换算的式子如下：

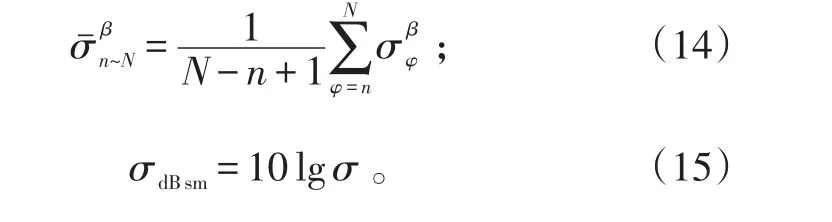
2 飞机RCS特性数值模拟

飞机RCS特性数值模拟包括：机翼参数化可调的飞机CATIA建模、飞机RCS特性数值模拟和机翼前缘后掠角对飞机RCS特性影响分析。

2.1 机翼参数化可调的飞机CATIA建模

本节应用CATIA软件，建立机翼参数化可调的飞机三维数字样机。飞机三维数字样机采用单座、双发、双立尾外倾、正常式布局的气动外形，采用带边条翼、翼身融合体的机身，并且采用机腹双进气道，2个武器弹舱内埋于机身的布局。

在机翼参数化可调的CATIA模型中，飞机机翼的翼身融合体弦长、翼尖弦长、翼展、机翼安装角、机翼翼型、前缘襟翼宽度、前缘襟翼长、襟副翼宽和襟副翼长均不变，机翼变化的仅有机翼前缘后掠角，机翼、前缘襟翼和襟副翼的约束关系，见式（1）~（10）。机翼参数化可调的飞机三维数字样机的基本尺寸见表1。由表1的基本尺寸数据，建立机翼参数化可调的飞机三维数字样机。基于此，对前缘后掠角参数进行变化，得出机翼前缘后掠角变化时飞机示意图（见图2）。

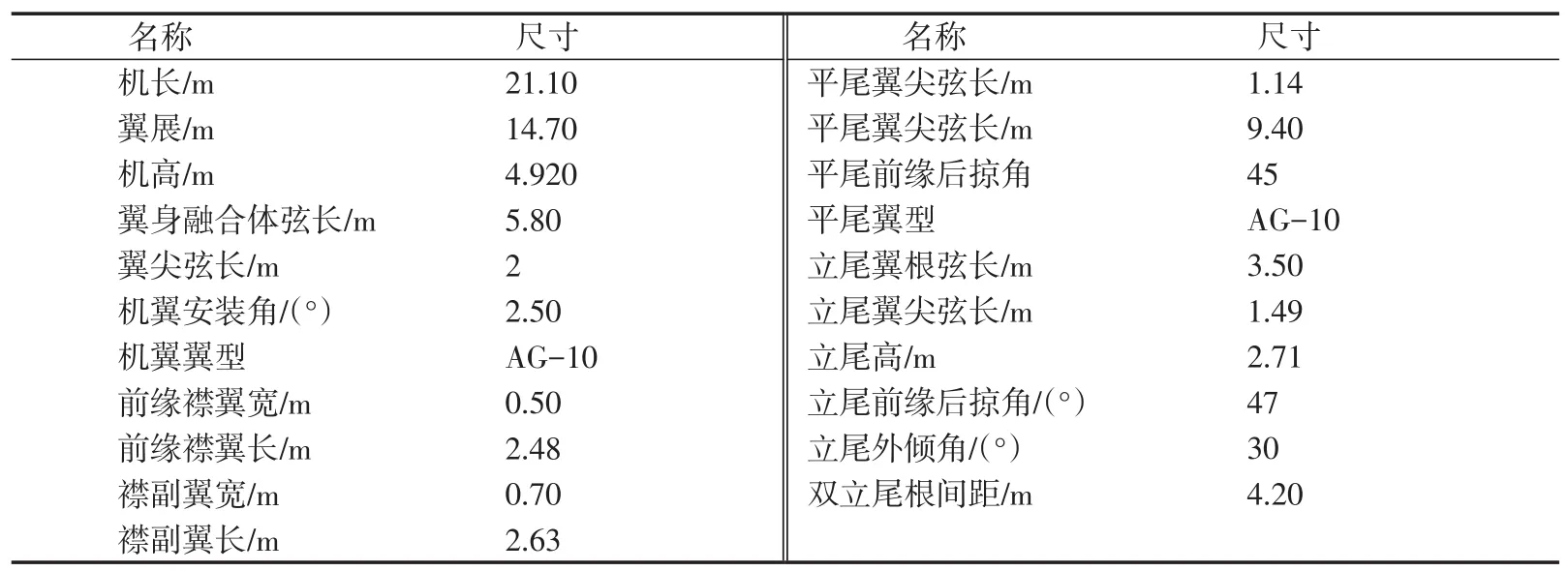
表1 飞机三维数字样机的基本尺寸数据Tab.1 Basic dimensions of the aircraft 3-D digital prototype

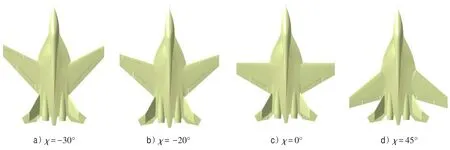
图2 机翼前缘后掠角变化时飞机示意图Fig.2 Schematic diagram of the changes in aircraft wing leading edge sweep angle

在使用CATIA软件建立完机翼参数化可调的三维数字样机后，将其转成后缀为stl格式的文件，导入RCSAnsys软件，进行飞机RCS特性数值模拟。

2.2 飞机RCS特性数值模拟

RCSAnsys软件是关于计算RCS特性的多年工作经验集大成之作，其方法的科学性和数值模拟的准确性经过微波暗室的大量的实验验证。本节使用RCSAnsys软件，使用X波段雷达，采用物理光学法和等效电磁流法，基于式（11）~（13），数值模拟机翼前缘后掠角变化时飞机的RCS强度分布（见图3），数值模拟χ=-30°时雷达入射波俯仰角在-15°、0°和15°时飞机的RCS特性（见图4）。

从图3 a）中可知：当机翼前缘后掠角χ为-30°时，在飞机方位角φ为30°的方位上，机翼左翼前缘的RCS强度分布较强。从图3 b）中可知：当χ=0°时，在φ=0°的方位上，机翼两翼前缘的RCS强度分布均较强。从图3 c）中可知：当χ=45°时，在φ=45°的方位上，机翼右翼前缘的RCS强度分布较强。

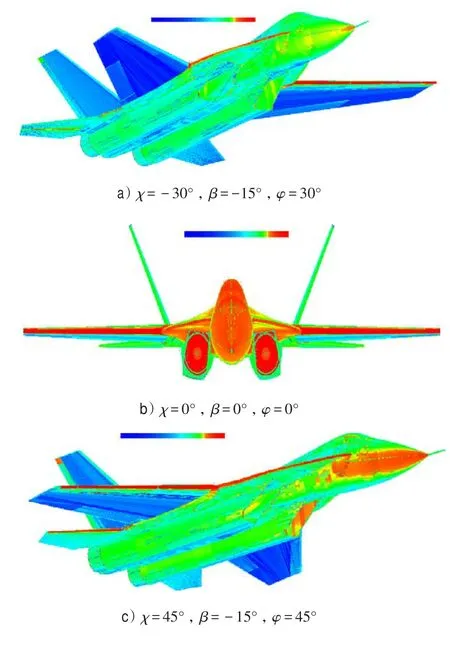
图3 机翼前缘后掠角变化时飞机RCS强度分布Fig.3 Aircraft RCS intensity distribution of the changes in aircraft wing leading edge sweep angle

从图4中可知，当机翼前缘后掠角χ为-30°、雷达入射波俯仰角β为-15°时，飞机的RCS在方位角φ为30°和-30°时有峰值，此时飞机的RCS的峰值为24.85dBsm，飞机头向±15°范围内RCS算术平均值0.74dBsm，飞机侧向±15°范围内RCS算术平均值dBsm，飞机尾向±15°范围内RCS算术平均值=1.74dBsm。

分析图3和图4可知，当飞机机翼前缘后掠角χ=-30°时，飞机在雷达入射波方位角φ为30°和-30°时均有峰值。

进而本节对图2中当χ={} -20°,0°,30°,45°,55°,时三维数字样机的RCS特性进行数值模拟，并进行分析，得出初步结论如下：飞机头向RCS峰值与机翼前缘后掠角有关，飞机头向RCS峰值之一的方位角与机翼前缘后掠角的角度相等。

2.3 机翼前缘后掠角对飞机RCS特性影响分析

本节对基于上节得出的初步结论进行深入研究。对机翼前缘后掠角χ在-30°至60°之间，以每隔5°变化一次，对飞机RCS进行数值模拟与分析。在机翼前缘后掠角对飞机RCS数值模拟过过程中，模拟机翼前缘后掠角不同的19架飞机，且模拟每架飞机在3种雷达入射波俯仰角（分别为-15°，0°，15°）条件下的RCS特性，共计得出57条飞机RCS特性曲线，得出20 520张飞机RCS强度分布图。本节对这些RCS特性曲线和强度分布情况进行数理统计与分析，得出飞机RCS头向峰值与机翼前缘后掠角的关系（见图5），得出飞机RCS头向峰值之一的方位角与机翼前缘后掠角的关系（见图6），得出飞机RCS头向算术平均值与机翼前缘后掠角的关系（见图7），得出在机翼前缘后掠角和雷达入射波俯仰角变化条件下飞机RCS的算术平均值（见表2）。表2为机翼前缘后掠角χ和雷达入射波俯仰角β变化条件下，飞机头向、侧向和尾向±15°范围内的RCS的算术平均值。

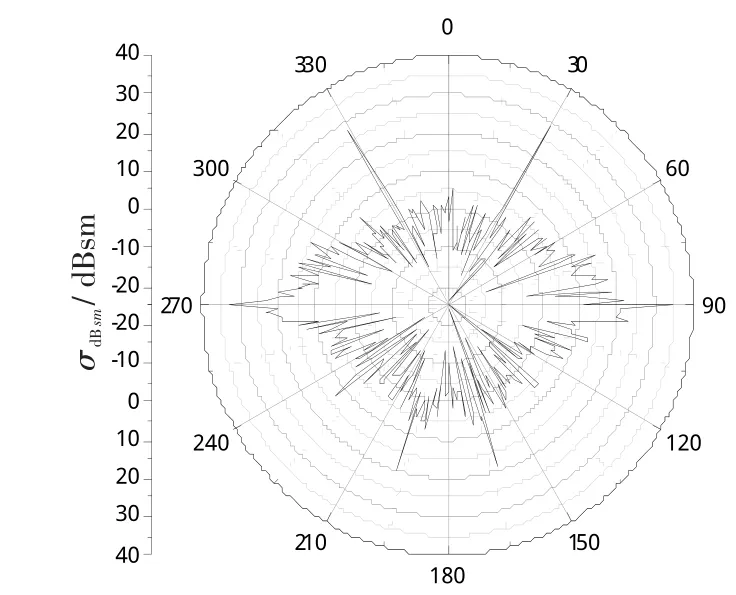
图4 在χ=-30°、β=-15°时飞机的RCS特性Fig.4 Aircraft RCS when conditions atχ=-30°、β=-15°

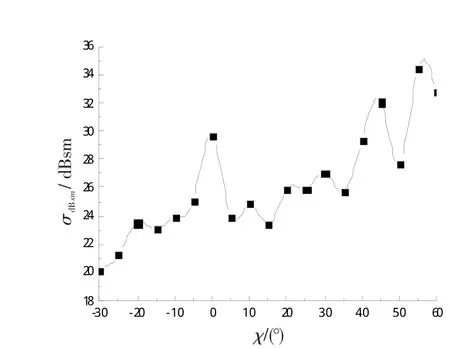
图5 飞机RCS头向峰值与χ的关系Fig.5 Relation of aircraft RCS forward peak andχ

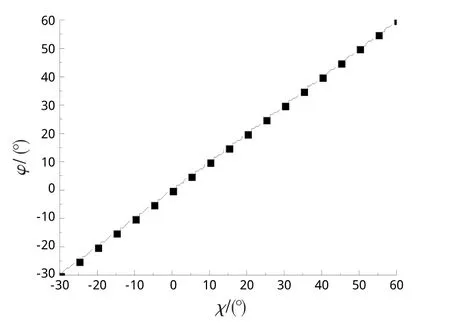
图6 飞机RCS头向峰值之一的方位角与χ关系Fig.6 Relation of aircraft RCSforward peak azimuth andχ

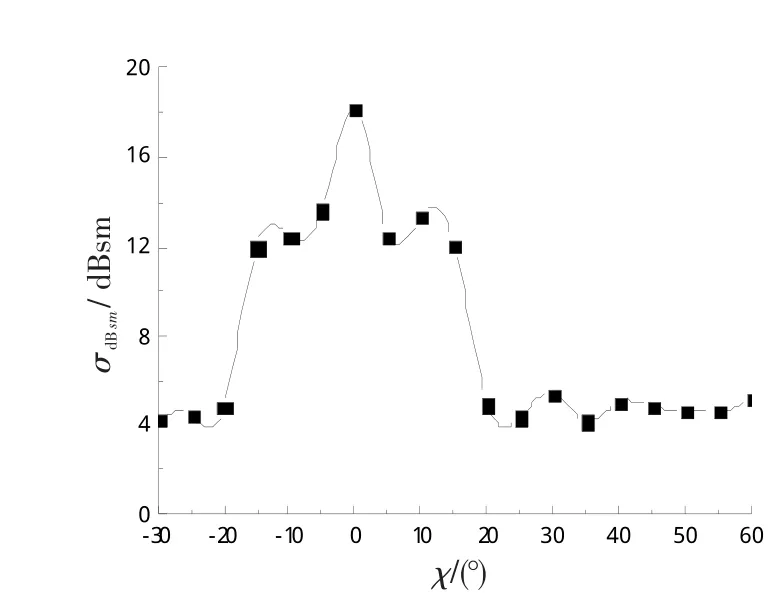
图7 飞机RCS头向算术平均值与χ关系Fig.7 Relation of aircraft RCS forward arithmetic average andχ

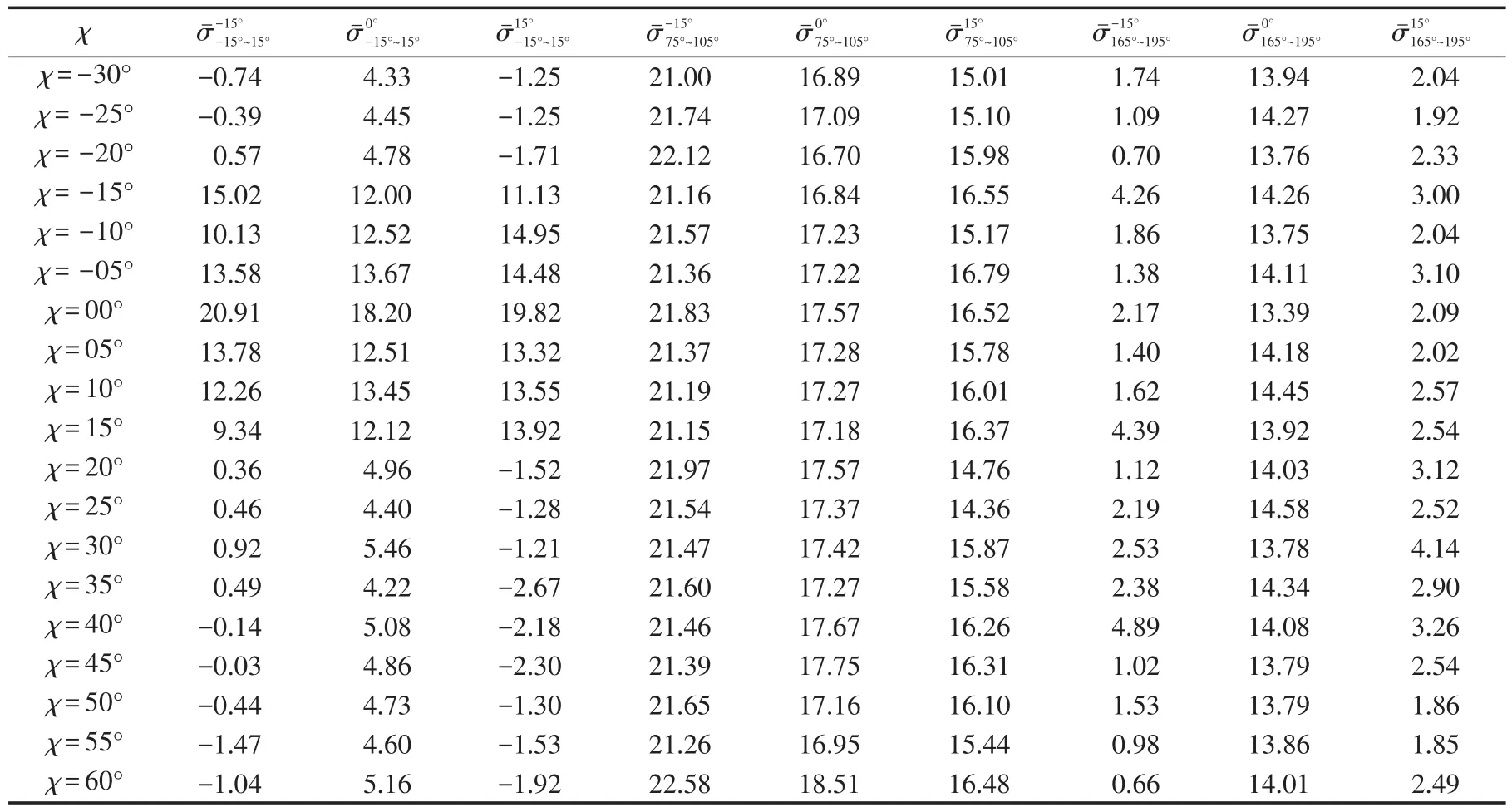
表2 在χ、β变化条件下飞机RCS的算术平均值Tab.2 Aircraft RCS arithmetic mean theχ、βunder changed conditionsdBsm

由图5可知，当机翼前缘后掠角χ为0°时，机翼为直机翼，其飞机RCS头向峰值为29.71 dBsm；当χ=-30°时，机翼为前掠翼，其飞机RCS头向峰值为20.14 dBsm，经单位换算，得出χ=-30°时飞机RCS头向峰值为χ=0°时飞机RCS头向峰值的11.04%；当χ=-20°时，机翼为前掠翼，其飞机RCS头向峰值为23.52 dBsm，经单位换算，得出χ=-20°时飞机RCS头向峰值为χ=0°时飞机RCS头向峰值的24.04%；当χ=30°时，机翼为后掠翼，其飞机RCS头向峰值为27.1 dBsm，经单位换算，得出χ=30°时飞机RCS头向峰值为χ=0°时飞机RCS头向峰值的54.82%；当χ=45°时，机翼为后掠翼，其飞机RCS头向峰值为32.09 dBsm，经单位换算，得出χ=45°时飞机RCS头向峰值为χ=0°时飞机RCS头向峰值的172.98%；当χ=55°时，机翼为大后掠翼，其飞机RCS头向峰值为34.45 dBsm，经单位换算，得出χ=55°时飞机RCS头向峰值为χ=0°时飞机RCS头向峰值的297.85%。

由图6可知，飞机RCS头向峰值之一的方位角角度与机翼前缘后掠角角度相等。

由图7可知，当雷达入射波俯仰角β为0°时，飞机头向±15°范围内RCS算术平均值为，当χ=0°时，=18.2 dBsm；当χ=-30°时=4.33 dBsm，经单位换算，当χ=-30°时为χ=0°时的4.10%；当χ=-20°时=4.78dBsm，经单位换算，当χ=-20°时为χ=0°时的4.54%；当χ=30°时，=5.46dBsm，经单位换算，当χ=30°时为χ=0°时的15.10%；当χ=45°时，=4.86dBsm，经单位换算，当χ=45°时为χ=0°时的4.63%；当χ=55°时，=4.60dBsm，经单位换算，当χ=55°时为χ=0°时的4.36%。

总之，由图5~7和表2的定量分析，可以得出以下定性分析结论：①飞机RCS头向峰值之一的方位角角度与机翼前缘后掠角角度相等；②在机翼前缘后掠角χ变化的条件下，雷达入射波俯仰角在-15°至+15°之间，飞机头向±15°范围内RCS算术平均值特性：直机翼大，前掠翼和后掠翼变小，大后掠翼更小；③在机翼前缘后掠角χ变化的条件下，雷达入射波俯仰角在-15°至+15°之间，飞机侧向和尾向±15°范围内RCS算术平均值特性：直机翼、前掠翼、后掠翼和大后掠翼的区别相对不大。

3 结论

本文采用物理光学法和等效电磁流法，对机翼参数化可调的三维数字飞机的CATIA模型进行RCS特性分析，分析了前掠翼、直机翼、后掠翼和大后掠翼飞机的RCS特性，并经过数理统计，得出以下结论：①采用机翼参数化约束模型可以分析在飞机设计中机翼前缘后掠角变化时RCS特性影响。②飞机头向RCS峰值之一的方位角与机翼前缘后掠角的角度相等。在χ变化的条件下，雷达入射波俯仰角在±15°之间，飞机头向方位角±15°范围内RCS算术平均值特性：直机翼大，前掠翼和后掠翼变小，大后掠翼更小；飞机侧向和尾向±15°内RCS算术平均值特性：直机翼、前掠翼、后掠翼和大后掠翼的区别相对不大。

本文研究的结果期望能对飞机总体设计与隐身技术的研究提供理论依据与技术支持。

[1]SURESH R PATEL，CHRISTOPHER L.F/A-22 vertical tail buffet strength certification，AIAA 2005-2292[R]. AIAA，2005.

[2]PAUL M BEVILAQUA.Genesis of the F-35 joint strike fighter[J].Journal ofAircraft，2009，46（6）：1825-1836.

[3]JOHN R.Configuration design development of the navy UCAS-D X-47B，AIAA2011-7041[R].AIAA，2011.

[4]知远.俄罗斯通向第五代战斗机的漫长道路[EB/OL].（2013-12-10）[2013-12-11].http：//mil.sohu.com/ 20131210/n391561165.shtml ZHI YUAN.Russia's long road leads to the fifth generation fighter[EB/OL].（2013-12-10）[2013-12-11].http：// mil.sohu.com/20131210/n391561165.shtml.（in Chinese）

[5]岳奎志，孙聪，刘虎.挂载导弹的作战飞机RCS特性数值模拟[EB/OL].（2013-11-05）[2013-12-10].http：// www.cnki.net/kcms/detail/11.2422.TN.20131105.1848. 001.html. YUE KUIZHI，SUN CONG，LIU HU.Numerical simulation on the RCS of combat aircraft for mounted missile [EB/OL].（2013-11-05）[2013-12-10].http：//www.cnki. net/kcms/detail/11.2422.TN.20131105.1848.001.html.（in Chinese）

[6]TOM R B.Optimization of aircraft configuration for minimum drag，AIAA-2010-3000[R].AIAA，2010.

[7]LI HUIYU，LI QI，XUE KAI.Research into Influence of Gaussian Beam on Terahertz Radar Cross Section of a Conducting Cylinder distribution[J].Journal of Infrared，Millimeter，and Terahertz Waves，2013，34（3）：289-298.

[8]LI YING，WU ZHE.A New Method for Analyzing Integrated Stealth Ability of Penetration Aircraft[J].Chinese Journal ofAeronautics，2010，23（2）：187-193.

[9]LEE D S，GONZALEZ L F，SRINIVAS K.Robust evolutionary algorithms for UAV/UCAV aerodynamic and RCS design optimization[J].Computers and Fluids，2007，37（5）：547-564.

[10]HUANG MINjIE，LV MINGYUN，HUANG JUN.Recognition of the major scattering sources on complex targets based on the high frequency radar cross section integrated calculation technique[J].Journal of Shanghai University，2009，13（4）：115-121.

[11]孙聪，张澎.先进战斗机对机载射频孔径系统隐身的需求及解决方案[J].航空学报，2008，29（6）：1472-1481. SUN CHONG，ZHANG PENG.Lo requirements and solutiona of avionics/RF system for advanced aircraft[J].Acta Aeronautica et Astronautica Sinica，2008，29（6）：1472-1481.（in Chinese）.

[12]LU JIANWEI，WANG QIANG.Aircraft-skin infrared radiation characteristics modeling and analysis[J].Chinese Journal ofAeronautics，2009，22（5）：493-497.

[13]PARK K K.RCS Prediction Acceleration and Reduction of Table Size for the Angular Division Algorithm[J].Journal of Electromagnetic Waves and Applications，2009，23（11-12）：1657-1664.

[14]阮颖铮.雷达截面与隐身技术[M].北京：国防工业出版社，1998：99-120. RUAN YINGZHENG.Radar cross section and stealth technology[M].Beijing：National Defense Industry Press，1998：99-120.（in Chinese）

Numerical Simulation of Wing Leading Edge Sweep Angle Under the RCS Influence

XU Ming1,ZUO Jun-wei1,YUE Kui-zhi2,YU Da-zhao2
（1.Naval Equipment Department,Beijing 100071,China; 2.Department of Airborne Vehicle Engineering,NAAU,Yantai Shandong 264001,China）

In this paper,the RCS characteristics of the aircraft 3-D digital prototype with a parametric adjustable wing leading edge sweep angle was studied，in order to improve stealth performance in the aircraft conceptual design.The CATIA was used to establish aircraft 3-D prototype.RCS Ansys and X-band radar were used to detect the aircraft based on physical optics and the equivalent electromagnetic flow method.In the radar incident wave pitch angle of-15°,0°and 15°,it conducted numerical simulation on RCS of the aircraft when the wing leading edge sweep angle varied between-30°and 60°.And then statistical analysis on the simulation results were conducted.In the condition of mutative wing leading edge sweep angle,the numerical simulation results of the aircraft RCS showed that the azimuth angle of the aircraft prior to the RCS peak equaled to the wing leading edge sweep angle and the features of the arithmetic mean of the aircraft prior to the RCS were that the bigger the straight wing,the smaller the forward-swept wing and swept wing and the even smaller the large swept wing,and relatively little change happed to the arithmetic mean value of the RCS of the aircraft lateral and tail.

aircraft conceptual design;leading edge sweep angle;stealth;physical optics method;numerical simulation

V221

A

1673-1522（2014）01-0047-06

10.7682/j.issn.1673-1522.2014.01.011

2013-10-15；

2013-12-12

国家自然科学基金资助项目（51375490）

徐鸣（1982-），男，工程师，大学。