或有补偿价值评估的期权定价模型

■王少豪

或有补偿是产生或有现金流的主要方式，大多产生在企业并购过程。对于与市场相关的或有补偿来说，由于其具有期权的性质，评估价值要困难得多。标准的折现现金流方法无法评估期权，对于大部分与市场相关的或有补偿，还是采用期权定价模型评估更有效。作者主要介绍了或有补偿价值评估期权定价模型解析方程的形式，并通过计算案例介绍数值方法的应用。

一、引子

在企业经营活动中，出现或有补偿的情况是大量存在的。笔者曾在文章《或有现金流的风险探讨》(刊于《中国资产评估》2014年4期)中得出这样的结论：或有现金流的风险要大于确定现金流的风险，而且采用传统的收益法无法确定其资本成本，所以只有采用期权定价理论来评估。或有补偿就是产生或有现金流的主要方式，它大多产生在企业并购过程，包括但不限于各种并购合同的对赌协议中。因为这样的或有补偿方式能够弥补买卖双方之间在当前和未来的价值分歧。这种或有补偿不仅对于买方来说具有一定的吸引力，而对于企业原来的所有者，也还是未来的经营者来说，同时也同样具有激励的作用。

二、两种不同的或有补偿有着不同的风险

评估或有补偿的时候，区分两种具有不同风险特征的不同类型补偿非常重要。其一是事件相关型的或有补偿，它主要是和企业某一既定目标的取得联系在一起。比如说企业的某一项科研实验的成功与否。这种类型的或有补偿风险主要呈现为非系统风险，它与经济范围领域的风险不相关。非系统风险可以通过多样化的投资组合分散或消除，这样就不需要掌握一个预期回报率的风险溢价。

另外一种或有补偿是市场相关型的补偿，这种补偿是建立在某个变量的基础上：如收购企业的经营销售收入，或EBIT，或利润，或公司在市场上普通股的股价。这种类型的或有补偿承担着系统性风险(贝塔风险)，与经济领域的风险有关。系统风险不能通过投资组合来分散或消除，因此需要掌控一个预期回报率的风险溢价。

对于事件相关型的或有补偿，系统风险为零。评估或有补偿只需要估算由此事件所产生的现金流、事件发生的概率、以及对方的信用风险。管理层可以提供取得事件相关目标的概率估计值，而评估师必须判断交易对方的信用风险。这种评估比起对于市场相关的或有补偿来说是非常简单和直接的。因为对于后者，系统风险和所要求的回报率的估算是非常具有挑战性的。本文讨论的主要是市场相关型的或有补偿评估。

三、或有补偿评估的期权定价模型

在BSM模型出来之前，研究人员可能有很好的方法来预测未来的现金流，但是他们在评估期权的时候却没有能力估算合适的折现率，所以唯一的方法还是采用期权定价模型。然而BSM模型是根据市场定价的金融资产在各种假设前提下推导出来的。对于不能满足假设前提的各种不同其他情况，必须要将BSM模型进行不同的修正，才能应用于各种不同的具体情况。

评估或有补偿就是这种具体情况，我们采用实物期权的评估方法。用实物期权这个词就意味着这个或有收益的标的资产不是市场定价的资产。比如说，息税前的销售收入或利润(EBIT)就是实物资产，而不是像普通股、债券以及某些商品等有市场定价的金融资产。本文中，实物资产与市场定价资产的关键区别在于：前者的预期增长率可以随着时间不同是任何值，或任何类型；而后者的增长率必须是与其风险及预期的回报率始终一致。比如说，一个公司销售收入的增长率可以是2.0%，5.0%，15.0%，或者是50.0%。一个实物资产三年的预期增长率可以是25.0%，而十年的预期增长率又可以是1.0%。而市场定价的金融资产其预期增长率必须和市场条件及其系统风险一致。换句话说，其交易的价格是与未来的期望值联系在一起的，所以他们的预期增长率是与无风险利率、系统风险的市场价格以及交易资产的系统风险相一致的。

尽管实物资产与金融资产之间有这样的区别，我们还是能够利用期权定价的方法较容易地评估出实物期权的价值。但这样做需要对标准的期权定价公式BSM模型作一个相对简单的修改。为了使评估师很好地理解BSM模型在实物期权评估中的修正，我们把这个过程分成几个步骤来解析，现详述如下。

(一)支付红利的修正

标准BSM模型的假设前提之一是：在衍生证券的有效期内没有红利支付。如以股票为例，现在红利的支付使得股票的价格在除权日的降低幅度等于红利的数额。所以如果红利收益率为q，那么红利的支付会使股票价格的增长率比不支付红利的股票增长率减少了q。如果支付连续红利收益率q的股票价格，从当前的S0增加到T时刻的ST，那么没有支付红利股票的价格将从当前的S0增加到T时刻的STeqT。换言之，也可以认为股票价格是从当前的S0e-qT增加到T时刻的ST。由此我们可以得出一个简单的修正方法：即当我们对有效期为T、支付已知红利收益率为q的股票的欧式期权进行估值时，我们可以将股票的现价从S0减少到S0e-qT，然后就像不支付红利股票的期权那样估值了。

即在BSM公式中以S0e-qT代替原方程中的S0，可以得出：

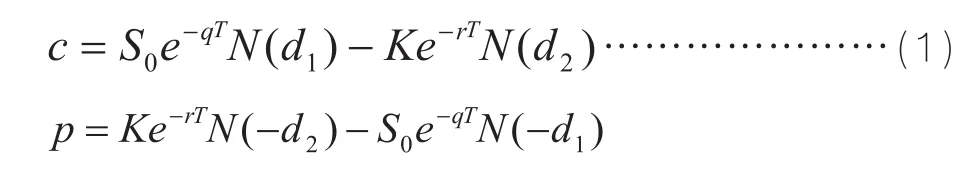
由于

所以

为了加深理解，我们可以说：如果没有红利，在风险中性的世界里，资本的收益率为无风险利率，即等于r。现在有红利，则在风险中性的世界里，资本和红利的共同收益率为无风险利率r。已知红利收益率为q，所以资本的收益率应该是(r－q)。如果股票的起始价格为S0，那么一个长度为T的时间步结束后股票的预期价格则应该是S0e(r-q)T。把这个期望值按无风险利率折现之后，得出的股票现价是：

这就是股票在风险中性世界里的起始价格。所以在运用BSM解析方程的时候要把它作为起始价格带入原来的标准公式，才有上面支付红利修正的期权定价方程。

这个支付红利股票的修正方程与实物期权的评估本无太多关系，只是在资源性资产的价值评估中采用这一方程，把矿产或石油资源的储量的开采作为红利的发放。因为如同股票的红利为股票的持有者创造了现金流却减少了股票的价值一样，自然资源的开采也是为所有者创造了现金流却减少了标的资产的价值。所以此时每年生产净收入占资源储量市场价值的百分比即为期权定价模型中的红利收益率。红利修正模型对后面的实物期权定价修正模型的解析方程还是具有一定的借鉴和启示作用。

(二)风险中性估值框架的扩展

实物期权的评估，不像股票红利那么简单。正如前面所说：实物期权所对应的标的资产不是股票债券等金融资产，而是不由市场定价的非贸易性资产。它的增长率可以是任意值，而不是与回报率相关的变量。但是正由于此资产具有期权的性质，所以估计各种实物期权的风险折现率十分困难，甚至是不可能的。因此我们不得不把定价金融资产期权的风险中性估值原理扩展到实物资产期权的定价上来。

为此，先定义一个变量θ的风险市场价格：

其中，r是无风险利率，μ是依附于θ的可交易证券的收益率，σ是其波动率。如果都是依附于变量θ，不管选择哪个可交易证券，我们得到的风险市场价格λ是相同的。在针对金融资产的传统风险中性世界里，风险的市场价格λ等于零。所以资产的收益率为无风险利率r。但对于实物资产来说，λ不等于零。

假设一个实物资产取决于多个变量。令mi和si为θi的预期增长率和波动率，那么

其中，zi是维纳过程。定义λi为θi的风险市场价格。我们可以扩展风险中性估值方法，依附于θi的任何资产可以按以下步骤估值：

①把每个θi的预期增长率从mi减少到mi－λisi；

②以无风险利率折现现金流。

至此，以上推导已经把风险中性估值框架从金融资产扩展到实物资产。对这些推导过程和结论的证明有兴趣的读者可以参见有关资料，如约翰·赫尔所著的《期货、期权及其他衍生产品》(第六版)等。评估师可以不了解理论推导过程而只需记住结论，那就是：实物期权的价值评估中，要从现实世界调整到风险中性世界，只需把实物资产在现实世界的增长率调整为风险中性世界的增长率，即：

风险中性世界增长率=现实世界增长率－风险市场价格×波动率

由于这是已经把实物资产的增长率调整到风险中性世界，那么将其期望值用无风险利率折现，就可以得到它的现时价值。这就是实物期权风险中性估值原理。

(三)风险中性期望值的求取

根据上面的两个步骤，调整实物资产预期增长率为风险中性增长率，可求出实物期权的风险中性期望值，把这个期望值用无风险利率折现，可得出期权价值。这是我们评估实物期权价值的方法之一，笔者在以前的案例中也应用过(见《中国资产评估》2013年第4期《期权定价模型评估对赌协议相关价值的探讨》)。如下：

我们设实物期权的变量为S，约定价格为K，期权有效期为T，则在风险中性世界到期时欧式买方期权的期望值为：

此处：

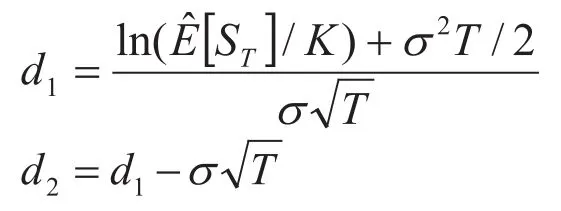
这里N()是累积标准正态分布值，σ表示主变量S的离散程度(标准差)。此外，是变量S在T时刻中性风险的期望值。由于已知风险中性的增长率等于现实增长率减去风险市场价格乘波动率，所以可得出此时的期望值为：

这里为习惯起见，还是设μ为变量S的现实世界期望增长率(这里的μ-λσ就是前面推导的m-λs)，λ还是市场风险价格。在传统风险中性世界中，假定所有风险市场价格都等于零。而对于实物期权来说，此时市场风险价格不再为零。因此，这个期望值是风险调节后的风险中性期望值。市场风险价格λ可以采用资本资产定价模型(CAPM)求出来。根据CAPM模型连续时间形式：

而

于是，风险的市场价格λ由下列方程给出：

此处，ρ是执行测度变量S变化百分比与股票市场组合价格指数收益之间的瞬态相关系数；参数σm表示市场组合指数收益率的波动率；μm表示市场组合指数的预期收益率。为了避免直接估算出上述相关系数ρ和波动率σm，我们可以采用风险系数β近似地替代，可得出风险中性的期望值。这种近似还是可信的，前提是企业运营的测量值如EBIT是以类似的方式与市场组合的权益价值相关。在这种情况下，风险中性的期望值如下式所列：

从而

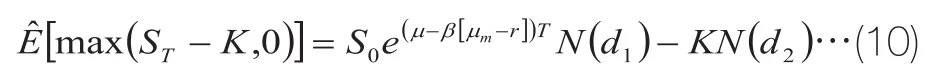
至此，求出风险中性的期望值之后，再用无风险利率折现可求出期权的价值：

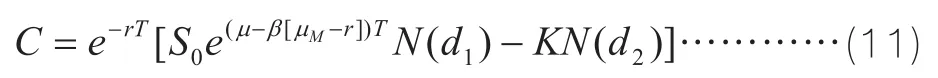
公式(11)就是我们针对实物期权所采用的布莱克-舒尔斯期权定价模型。对于对赌协议以及或有补偿都可以采用这个方程。式中d1和d2的含义和上面公式(5)一样。

(四)直观解析方程的修正

(11)式虽然可以作为实物期权评估的计算模型，但是这个模型的缺陷是必须先求出风险中性的期望值，然后再折现。即使像上面的(11)式已经展开，但是在计算d1和d2的时候还是要先求期望值。这对于习惯于BSM模型解析方程的评估师来说，似乎有些别扭。于是有人就想出把实物期权评估的BSM方程修正为直观解析方程的形式。公式如下：

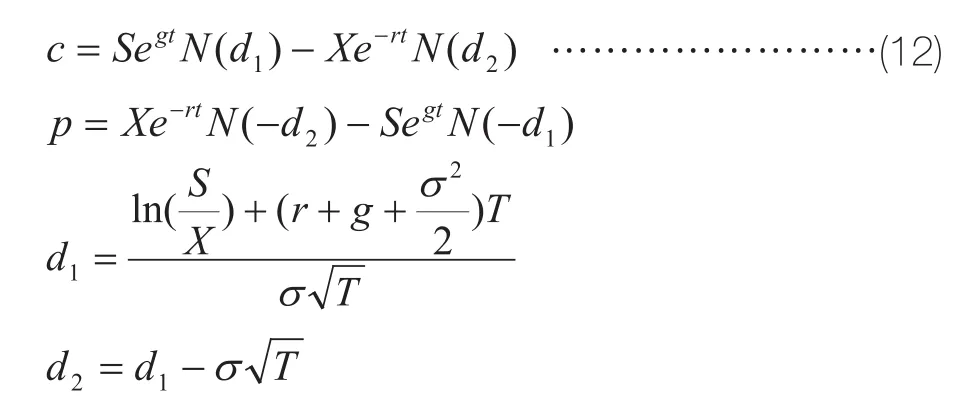
这个公式看起来类似于连续支付红利的改动模型，见公式(1)。只不过原来支付红利修正模型中的红利收益率q，在这里变成了－g。也就是原来的股票收益率(r－q)变成了实物资产期权定价公式中的回报率(r+g)。 这里的g是我们新设定的一个变量，它等于实物资产现实世界的期望增长率减去实物资产所需的回报率。即：

这里μ还是实物资产在现实世界的期望增长率，而RS则是实物资产所需的回报率。上面的修正模型可以用BSM的微分方程推导出这个解析结果，也可以采用代数式推导并结合连续支付红利修正模型的比较，得出这个结果。过程如下：

已知股票支付红利时，股票现价为：

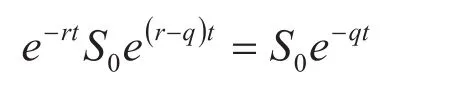
这是股票在风险中性世界里的起始价格。在运用BSM解析方程的时候要把它作为起始价格带入原来的标准公式，才有上面支付红利修正的期权定价方程。

参照股票支付红利时的现价计算，现在实物资产的期望值折现应该是：

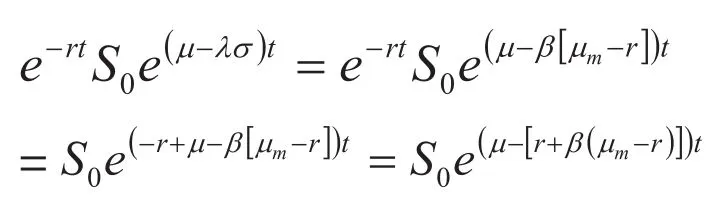
将上面幂指数化简：

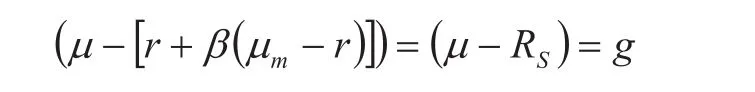
因为根据资本资产定价模型(CAPM)，实物资产所需的回报率等于：

所以，实物资产的期望值折现应该是：

在BSM公式中，以S0egt代替原方程中的S0，就可以得出上面实物期权评估的BSM修正模型，见公式(12)。

四、或有补偿计算案例

(一)案例一

我们先用一个简单的计算实例来演示上述解析方程的计算结果，本例中有两个或有补偿都是基于销售收入的。一个补偿是在销售收入超过1053万元时，另一个是收入超过1500万元时，实际上是两个不同约定价格的期权。目前公司的销售收入水平是2000万元，第二年预计以15%的增长率增长，波动率为30%，无风险利率是2%，市场风险溢价是7%，销售收入的贝塔值为1.50。这样，根据CAPM模型，销售收入所要求的回报率就是：12.5%=2.0%+1.50×(7.0%)。而公式(12)中的g为2.5%=15%－12.5%，即实物资产增长率减去实物资产所需的回报率。

这两个或有补偿价值的计算过程见表1。

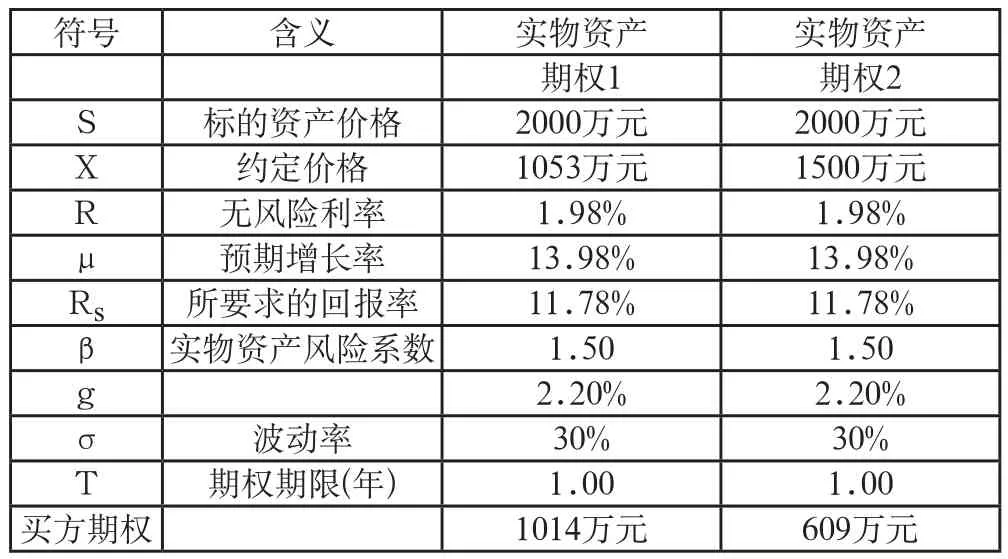
表1 基于销售收入的或有补偿价值评估

(二)公式计算中参数的考虑

1．关于连续复利

由表1可以看出，无风险利率、增长率等都不同于所给出的数值。这是为了满足BSM公式的要求，把所有的回报率都由原来的离散值转换为连续值，无风险利率由2.0%转换为1.98%；标的资产回报率由12.5%转换为11.78%；g由原来的2.5%转换为2.20%。

由于我们在很多投资或财务的计算中，利率都是按离散利率计算。假设数额A以年利率R投资了n年，利率按每一年计一次复利计算，则以上投资的终值为：

但如果每年计m次复利，则该投资的终值为：

当复利频率m趋于无穷大时，就称为连续复利(continuous compounding )。在连续复利的情况下，数额A以年利率R投资了n年，终值为：

这个连续复利的计算结果，从大部分实用目的来看，和每天计算复利的结果是一样的。所以通常认为连续复利与每天计复利等价。对于一笔以利率R连续复利n年的资金，其结果是乘上eRn。而对一笔以利率R连续复利贴现n年的资金，则应乘上e-Rn。

评估师平常所应用的多半是离散利率，且多为一年计一次复利。但在期权以及其他复杂衍生证券定价时，连续复利得到广泛应用。如BSM方程，或二项数期权定价公式中均是以连续复利表示。所以笔者认为，在实物期权的应用计算中有必要把评估中得到的离散利率转换为连续利率，再应用到期权定价的各种公式中。

为此，我们可以很容易地推导出两者的转换公式。设连续利率为RC，Rm是与之等价的每年计m次复利的利率，可以得出：

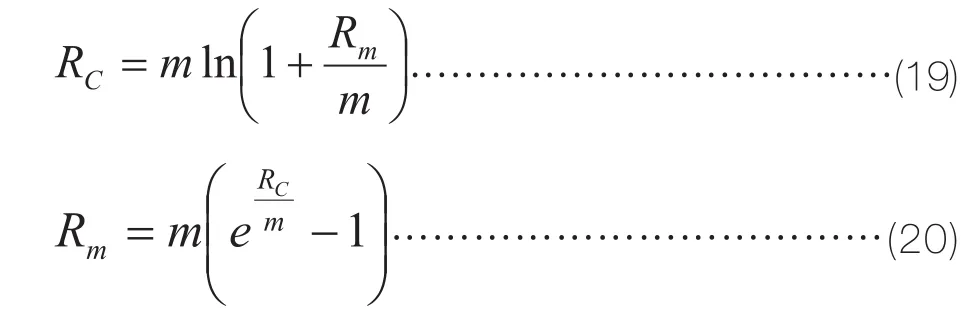
我们把这些公式设在Excel表里面的单元格中，可以得到上面各种利率的换算结果。无风险利率由2.0%转换为1.98%；标的资产回报率由12.5%转换为11.78%；g由原来的2.5%转换为2.20%。

2．关于实物资产的风险系数

在某些情况下，实物期权的方法的确是特别有用。然而笔者绝不认为对于或有补偿的评估，实物期权方法是唯一合理的方法。其他的方法，比如概率加权预期收益法也是非常有效的。但一般在或有补偿的价值相对较大、并其支付的期限相对较长、期权不是深度实质期权且系统风险不是接近于零的情况下，期权方法多半是最有价值的方法。

确定是否采用实物期权的方法来评估或有补偿的价值应该包括概念上的判断和实证的挑战两方面。概念上的判断主要是看评估或有补偿的时候，运用BSM的假设条件是否符合得出公允市场价值的概念。很多准则定义公允市场价值为：市场交易双方在评估基准日，为有序交易所得到的资产或债务的转移所付出的价格。而或有补偿以及它们所对应的资产往往不是被交易的资产，而任何价值评估总是建立在不可观察的输入数据之上的，好像并不十分符合公允市场价值的概念。但是由于大部分情况下具有期权性质的资产无法采用常规评估方法得出结果，所以笔者仍然认为对或有补偿或其他员工期权定价时，还是要优先采用期权定价的方法。实际上，在一些有影响力的准则，如AICPA操作指南的股权价值评估部分上面就写道：BSM方程在评估复杂资本结构的私人公司的某些权益或其它资产的时候可以作为一个可接受的评估方法。

实证上的挑战包括估算对应或有补偿资产的波动率和系统风险。也就是在解析方程中需要输入的参数β和σ。这里需要注意的是这个波动率和系统风险是标的资产的，而不是公司或公司权益的。如果标的资产是EBIT，则是指EBIT的贝塔值，如果标的资产是销售收入，则是指销售收入的贝塔值。求取标的资产的贝塔值可以采用直接法和间接法。直接法就是采用资产的价值变动数据和市场的指数变动数据进行回归分析。美国普华永道的分析师曾针对两种普通的对应资产——EBIT和销售收入，利用2001到2010十年间122家美国最大的非金融上市公司的季度财务数据和市场回报率的数据，来估算其波动率和系统风险等参数，结果并不理想。这些结果的最后解释是：这种用来估算贝塔值的数据和方法都是不适当的，不能分辨真实的系统风险。如果有更有效的经济学方法，或更好的数据是可以得出完全不同的结果的。

在运用期权定价模型估算实物资产的时候，笔者认为采用间接法来估算他们的贝塔值更合适。即在公司权益贝塔值的基础上估算EBIT和销售收入的贝塔值。因为公司权益的贝塔值在很多地方都可以查询得到。它是一个公司净收益贝塔值很好的代用品，因为净收益是度量公司股权收益的最好指标。同样，笔者认为公司资产的贝塔值是EBIT贝塔值的最好替代品。计算公司的资产贝塔值有标准的方法，即从权益贝塔值入手，调整债务效应的财务杠杆。利用Hamada公式的方法，资产的贝塔值ßA是权益贝塔值ßE除以调整负债权益比D/E和税率t的一个系数而得出，即：

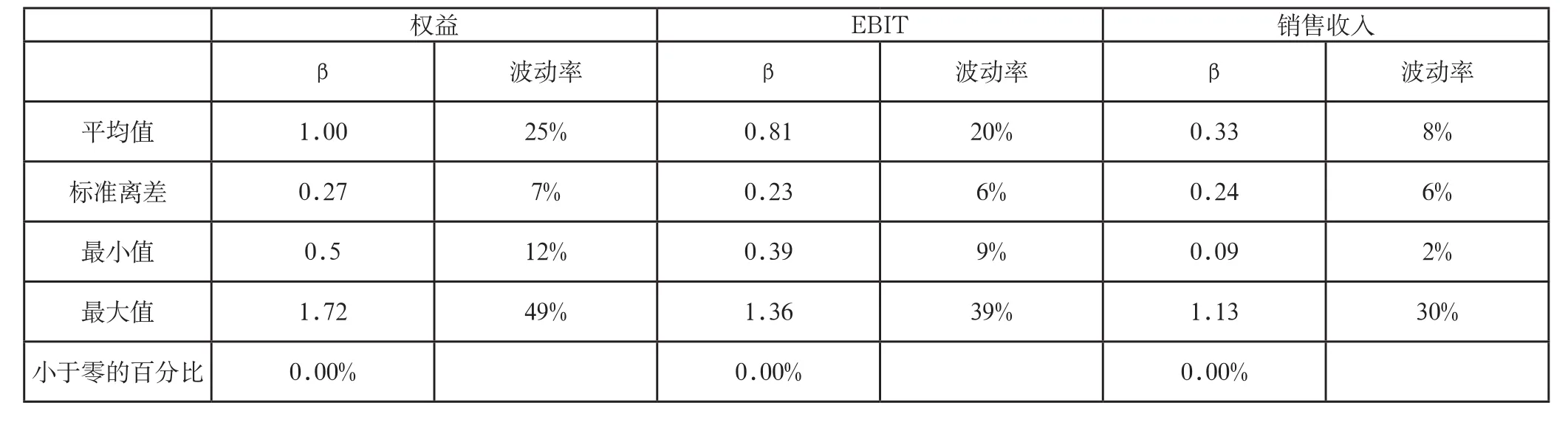
表2 间接法通过权益贝塔值估算EBIT和销售的贝塔值和波动率

同样，也存在一个类似的方法来计算公司销售收入的贝塔值。即通过EBIT的贝塔值调整经营杠杆而得出。布雷利、梅耶斯和阿伦给出公式：销售收入的贝塔值ßR等于资产贝塔值经过调整经营杠杆而得出，这个调整即是通过一个比例：固定成本的现值PVF比资产的现值PVA：

表2给出的是分析师对122个美国非金融公司采用上述调整计算资产和销售的贝塔值以及波动率而得出的实证分析结果。根据固定成本和EBIT资本化以后的相对价值来计算PVF和PVA，时间也是从2001年到2011年共十年，固定成本用国债利率进行资本化，而EBIT则用资本成本来资本化。

笔者相信这些结果是估算EBIT和销售收入系统风险更为一致和可靠的估计值。虽然这些结果很有意义，但在实施去杠杆的操作上却遇到很大挑战。一般来说，要把成本很清楚地分为固定成本和可变成本并不是那么容易的事情。特别是或有补偿可以是很短时期，也可以是很长时期，一个短期内或有补偿的固定成本对于长期或有补偿可能是可变成本。

笔者认为销售收入的进货成本是关键的可变成本，而销售成本和管理成本是主要的固定成本。对于这个问题，虽然没有严格理论上的答案，但在实践中可以大致划分为固定成本和可变成本，以便合理地估算出销售的系统风险。很多时候，估算的或有补偿的价值对于固定成本和可变成本的划分并不十分敏感。基于上述统计的结果和对私人公司和项目具体分析的经验，相信采用这样方法估算EBIT和销售收入贝塔值和波动率在应用期权方法评估或有补偿价值中是可行的。

(三)案例二

为加强评估师应用期权定价模型评估或有补偿价值的印象，在上述案例一的基础上，再给出公司A和公司B两个或有补偿价值应用修改后的BSM买方期权定价公式评估案例。

两个公司或有补偿都取决于第二年的销售收入水平。当年的销售收入是一亿，预计以后两年年增长率均为22%，销售收入的波动率是30%，无风险利率是2%。或有补偿分为两步：(1)如果第二年销售收入超过2亿，给一个固定支付500万；(2)如销售超2亿，超出2亿部分的销售收入提成20%作为可变支付。对两个公司评估或有补偿，公司A销售贝塔值为0，公司B销售贝塔值为0.5。市场风险溢价是7%。表3给出了或有补偿的价值以及他们的计算过程。

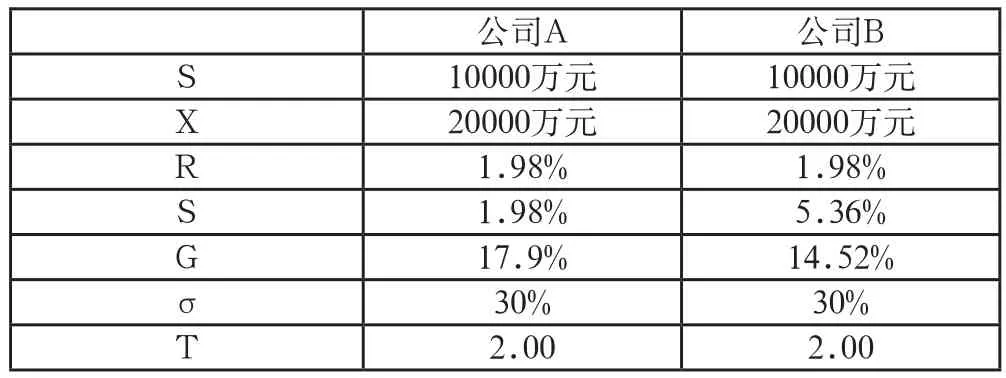
表3 评估两个公司以销售收入为基础的或有补偿

上述表格是电子表格的显示。实际上，我们已经很熟悉采用Excel来进行各种运算。把计算公式输入到单元格即可。对于这两部分的或有补偿，第一部分的固定支付是我们经常遇到的一种支付形式，它是一个典型的两值期权。

这种情况可对应于一个不连续的二值买权。这样一个“现金或无价值”的看涨期权会应允一个固定的支付Q，条件是如果企业运营指标在到期日超过一定的门槛值X的话。现在X=20000万元，而固定支付额Q=500万元，即如果两年后的销售收入超过20000 时，则卖方可收到一个500万元的固定支付款，否则收入为零。

可应用两值期权的方程如下：

这里d与前面公式(12)中含义一致。

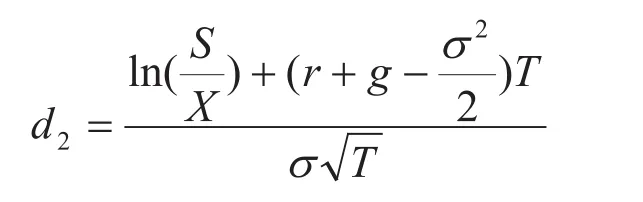
所以，计算得出：对于公司A，N(d2)=0.182。对于公司B，N(d2)=0.143。由此估算这个两值期权的价值分别为：87万和69万元。

与销售收入挂钩超过2亿后的20%提成就是一个典型的买方期权。这个或有补偿的支付价值计算是根据修改后的BSM公式(12)计算出来的，分别为200万和146万。从两个公司的计算结果来看，主要是公司B的销售系统风险降低了两种类型或有补偿支付的价值。

五、结语

当或有补偿的风险与市场无关时，我们可以采用收益法相对直接地评估出或有补偿的价值。即估算或有补偿预期的现金流以及它们的折现率，由资本资产定价模型求出。但对于与市场相关的或有补偿来说，由于其具有期权的性质，评估价值则要困难得多。标准的折现现金流方法无法评估期权，所以对于大部分与市场相关的或有补偿而言还是采用期权定价模型评估更为有效。

期权定价模型方法已经广泛应用于非贸易型金融工具，如ESOP，复杂的激励奖金，嵌入式衍生品和复杂资本结构等，它非常灵活且具有适应性。采用BSM解析方程，也可采用数值方法来评估更复杂的支付形式。特别是蒙特卡洛模拟适合于处理那些交互相关的金融指标，有些或有补偿常常发现这些指标。本文主要是介绍解析方程的形式，以后有机会再介绍一些数值方法的计算案例。

[1]约翰·赫尔.期权、期货及其他衍生产品(第六版).人民邮电出版社,2009年.

[2]理查德·布雷利,斯图尔特·迈尔斯.资本投资与估值.中国人民大学出版社,2010年.

[3]R.S.Hamada.“The Effect of the Firm’s Capital Structure on the Systematic Risk of Common Stocks”.Journal of Finnace,27(1972)435-452.

[4]Richard Brealy,Stewart Myers,and Franklin Allen.Principals of Corporate Finnace(8th edition).New York:McGraw Hill Irwin.2006.