Hartley变换在位场(重、磁)异常导数计算中的应用

马国庆，黄大年，杜晓娟，李丽丽

吉林大学地球探测科学与技术学院，长春 130061

Hartley变换在位场(重、磁)异常导数计算中的应用

马国庆，黄大年，杜晓娟，李丽丽

吉林大学地球探测科学与技术学院，长春 130061

导数计算是位场(重磁)数据处理中必不可少的技术手段，现今大多采用Fourier变换来进行。Hartley变换是在Fourier变换基础上定义的一种实数域运算，比Fourier变换更加对称，所需的运算量更少。笔者推导出基于Hartley变换的重磁异常导数计算公式，计算结果与理论值之间误差小于5%，通过理论模型证明Hartley变换可替代Fourier变换进行位场异常的导数计算，且受噪音干扰较小。将Hartley变换用于位场边界识别滤波器的计算，获得了清晰的断裂分布。

位场；导数； Fourier变换；Hartley变换

0 引言

导数计算被广泛应用于重磁数据的处理与解释[1-3]，具有突出浅源异常、区分叠加异常、确定地质体边界以及削弱背景异常的作用。现今大多采用Fourier变换[4]来完成重磁异常导数的计算。Fourier变换要求数据的尺寸为2的幂次，而Hartley变换无此要求。Hartley变换是在Fourier变换基础上定义的一种实数域内的运算[5]，至少比Fourier变换减少一半的空间和时间[6]，且更加对称。Hartley变换已经在图像处理、模式识别、地震波场模拟等领域得到广泛应用[7-11]；在位场数据处理中最早被用来进行波谱分析[12-13]，其得到的异常波谱也能成功地区分出背景场和局部场。Sundarajan等[14]将Hartley变换与Hilbert变换相结合进行功率谱分析，并证明采用该方法所需的计算量相对Fourier变换要少。后来人们利用Hartley变换进行位场剖面数据的相关分析与分量之间的转换[15-16]，均取得了较好的应用效果。

笔者根据Hartley变换的基本性质及位场基本原理推导出基于Hartley变换的重磁异常二维和三维导数计算公式。通过理论模型试验证明Hartley变换计算得到的导数与Fourier变换计算结果相接近，且与理论值误差较小，可作为进行位场数据处理与转换的另一种方法。

1 二维重(磁)异常频谱及导数计算公式推导

1.1 一维Hartley变换的定义

Hartley变换是酉变换的一种，变换前后的信号熵和能量不变[5]。Hartley变换的一维形式如下:

正变换为

(1)

逆变换为

(2)

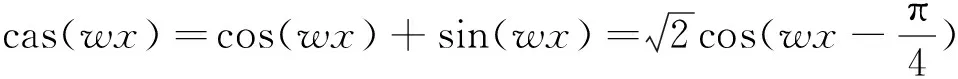
由Hartley变换定义奇函数与偶函数如下:

奇函数为

(3)

偶函数为

(4)

1.2 一维Hartley变换的性质

性质1：Hartley变换与自身奇函数和偶函数的关系[5-6]为

(5)

(6)

性质2：Hartley变换与Fourier变换的关系式为

(7)

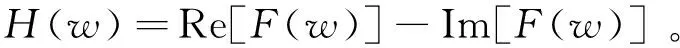
(8)

(9)

式中：PH(w)、XH(w)分别为pxy(τ)、x(t)的Hartley变换；YHe(w)、YHo(w)分别为y(t)的偶函数变换和奇函数变换。

(10)

1.3 二维重磁异常Hartley谱及导数计算公式

重力场源在z≤0空间中的重力异常f(x,z)是调和函数。已知z=0(水平面上)的函数值f(ξ,0)，求z≤0空间中的重力函数值f(x,z)，这种数学问题为狄里希莱(Dirichlet)问题(第一边值问题)。利用格林函数可求得上半空间解的积分表达式。对于二维问题，延拓积分表达式为[17]

(11)

已知Fourier变换关系式[18]：

(12)

(13)

由性质3可得f(x,z)的Hartley变换式为

(14)

式中，FH(u,0)为f(x,0)的Hartley变换。

对式(14)进行反Hartley变换可得

(15)

应用微分定理对式(15)做积分号下求微分的计算，即可求出重、磁异常导数的表达式。

水平导数：

(16)

垂直导数：

(17)

从式(16)和(17)中可以看出，Hartley在进行导数计算时，均是实数域内的运算，不需要虚数参与计算,因此比Fourier变换减少一半的运算量。

2 三维重(磁)异常Hartley谱及导数计算公式推导

2.1 二维Hartley变换的定义

Hartley变换二维形式与二维Fourier变换不同。对于二维实函数的Hartley变换[9]，其积分核存在2种形式：cas(ux+vy)、cas(ux)cas(vy)。为了便于计算，笔者采取可分离的第二种形式，并有如下的正、逆变换表示式为

(18)

(19)

对于二维Hartley变换也可以构造出奇、偶函数，其形式如下:

奇函数为

(20)

偶函数为

(21)

2.2 二维Hartley变换的基本性质

性质5：二维Hartley变换与Fourier变换的关系式为

(22)

性质6：二维Hartley变换的褶积关系式为

(23)

(24)

2.3 三维重(磁)异常Hartley谱及导数计算公式

重力场源在z≤0空间中的重力异常f(x,y,z)是调和函数。对于三维问题，延拓积分表达式为

(25)

a.一阶水平导数；b.未扩边一阶垂直导数；c.扩边后一阶垂直导数；d.二阶垂直导数。图1 不同方法计算的重力异常导数结果Fig.1 The derivative results of gravity anomaly computed by different methods

a.理论重力异常；b.理论一阶垂直导数；c.利用Fourier变换计算得到的一阶垂直导数；d.利用Hartley变换计算得到的一阶垂直导数；e.Fourier变换计算导数与理论导数差；f.Hartley变换计算导数与理论导数差；g.Fourier变换计算得到的含噪异常的一阶垂直导数；h.Hartley变换计算得到的含噪异常计算得到的一阶垂直导数。图2 长方体产生的重力异常及其导数计算结果Fig.2 Gravity anomaly and derivative data generated by rectangular prism

已知Fourier关系式[18]：

(26)

由性质5可得

(27)

(28)

因此，φ(ε,η)的Hartley变换为

(29)

由性质6可得，f(x,y,z)的Hartley变换式为

(30)

式中：FH(u,v,z)为f(x,y,z)的Hartley变换，FH(u,v,0)为f(x,y,0)的Hartley变换。

对式(30)进行反Hartley变换可得

(31)

应用微分定理对式(31)做积分号下求微分运算，即可求出重、磁异常导数的表达式。

x方向导数：

(32)

y方向导数：

(33)

z方向导数：

(34)

从式(32)、(33)和(34)中可以看出，三维导数计算公式与二维导数计算公式的推导过程不同，但最终的导数形式是一致的。

3 理论模型试验

以二维情况为例：水平无限延伸圆柱体半径R=50 m，中心点埋深h=100 m，与围岩密度差ρ=1 g/cm3。分别利用离散Fourier和离散Hartley变换计算z=0观测面上重力异常的导数(图1)，并统计2种方法计算得到的导数与理论导数之间的均方差(表1)。

从表1中可以看出，采用Hartley变换计算得到的垂直导数的精度要略高于Fourier变换计算结果的精度，可作为位场导数计算的另一种选择。

表1 不同方法计算导数与理论导数的均方差

Table 1 The error between theoretical derivative and computed derivative by different methods

Fourier变换Hartley变换一阶水平导数2.04×10-63.41×10-6一阶垂直导数2.86×10-52.68×10-5二阶垂直导数1.33×10-32.72×10-4

噪声是实际数据处理中不可避免的影响因素，试验Hartley变换和Fourier变换在存在噪声情况下的导数计算效果。图2为埋深分别为15 m和20 m的长方体产生的重力异常。从图2中可以看出，Hartley变换计算结果的幅值与理论值更为接近。从图2g、h可以看出，Hartley变换受噪音干扰较小，依旧能很好地完成导数的计算，而Fourier变换的导数结果受噪音影响相对较大。这主要是由于在频率域中转换因子具有明显的噪声放大作用[19]，而Hartley变换为实数域内的运算，不会明显地增大噪声的干扰。

4 实际数据应用

为了进一步试验本文方法的计算效果，分别利用Hartley变换与Fourier变换完成边界识别滤波器-增强型Ө图(enhanced theta map,ETM)[20]的计算，其表达式为

ETM=

(35)

式中，mean代表均值。利用不同方法计算得到的增强型Ө图对中国西北部朱日和地区磁异常进行边界识别处理，计算结果(图3)均可以清晰地反映出地层之间的界限。

5 结论

Hartley变换是在Fourier变换基础上定义的一种实数域计算，笔者推导出了基于Hartley变换的位场(重、磁)异常导数计算公式。通过理论模型试验证明，Hartley变换计算结果与Fourier变换计算结果接近，与理论值之间误差较小。将Hartley变换和Fourier变换应用于位场数据边界识别滤波器的计算，均能清晰地获得地层之间的界限特征，因此,Hartley变换可作为位场数据处理与转换的另一种选择。

[1] 马国庆，杜晓娟，李丽丽. 利用水平与垂直导数的相关系数进行位场数据的边界识别[J]. 吉林大学学报：地球科学版， 2011, 41(增刊1): 345-348. Ma Guoqing, Du Xiaojuan, Li Lili. Edge Detection of Potential Field Data Using Correlation Coefficients of Horizontal and Vertical Derivatives[J]. Journal of Jilin University: Earth Science Edition, 2011, 41(Sup.1): 345-348.

[2] Ma G, Li L. Edge Detection in Potential Fields with the Normalized Total Horizontal Derivative[J]. Computers & Geosciences, 2012, 41: 83-87.

[3] 马国庆，杜晓娟，李丽丽．解释位场全张量数据的张量局部波数法及其与常规局部波数法的比较[J]．地球物理学报，2012，55(7)：2450-2461. Ma Guoqing, Du Xiaojuan, Li Lili. Comparison of the Tensor Local Wavenumber Method with the Conventional Local Wavenumber Method for Interpretation of Total Tensor Data of Potential Fields[J]. Chinese Journal of Geophysics, 2012，55(7)：2450-2461.

[4] Blakely R J. Potential Theory in Gravity and Magnetic Applications[M].Cambridge: Cambridge University Press, 1996: 256.

[5] Harteley R V L. A More Symmetrical Fourier Anal-ysis Applied to Transmission Problems[J]. Proc IRE, 1942, 30(2): 144-150.

[6] 余品能，路凌云.离散Hartley变换的一种快速递归算法[J].石油地球物理勘探，1998，33(5)：591-596. Yu Pinneng, Lu Lingyun. A Fast Recursive Algorithm of Discrete Hartley Transform[J]. Oil Geophysical Prospecting，1998，33(5)：591-596.

[7] 彭军，罗奇峰. Hartley变换在地震波研究中的应用[J].国际地震动态，2008(12)：6-8. Peng Jun, Luo Qifeng. The Application of Hartley Transform to the Study on Seismic Wave[J]. Recent Developments in World Seismolog, 2008(12)：6-8.

[8] 余品能，蒋增荣．图像及数字信号处理中的快速算法研究进展[J]．高校应用教学学报：A辑，1991， 6(2)：302-316. Yu Pinneng, Jiang Zengrong. Advances in the Study of Fast Algorithms in Image and Digital Signal Processing[J]. Applied Mathematics: A Journal of Chinese Universities, 1991，6(2)：302-316.

[9] 甘利灯．哈特莱变换及其性质[J]．石油地球物理勘探，1992，27(5)：605-616. Gan Lideng. Hartley Transform and Its Prosperities[J]. Oil Geophysics Prospecting, 1992，27(5)：605-616.

[10] 周辉，何樵登．利用Hartley变换模拟各向异性介质地震波场[J]．石油地球物理勘探，1995，30(5)：593-601. Zhou Hui, He Qiaodeng. Seismic Wave Modeling in Anisotropic Medium by Hartley Transform[J]. Oil Geophysics Prospecting, 1995，30(5)：593-601.

[11] Saatcilar R. The Use of Hartley Transform in Geo-physical Applications[J]. Geophysics,1990, 55(11):1488-1495.

[12] Bravo R, Escalona O, Mora F, et al. Vector Spectral Combination of Orthogonal Leads Using the Hartley Transform for Late Potential Analysis in Chagas Disease[J]. Computers in Cardiology, 1997, 10:415-417.

[13] Mansour A, Garni A, Narasimman S . Hartley Spectral Analysis of Self-Potential Anomalies Caused by a 2-D Horizontal Circular Cylinder[J]. Arabian Journal of Geosciences, 2012, 5(6): 1341-1346.

[14] Sundararajan N, Srinivas Y. Fourier-Hilbert Versus Hartley-Hilbert Transform with Some Geophysical Applications[J]. Journal of Applied Geophysics, 2010,71(4):157-161.

[15] 魏雅利, 骆遥.基于Hartle变换的剖面位场转换[J]. 地球物理学进展, 2010,25(6): 2102-2108. Wei Yali, Luo Yao. 2D Potential Field Transformation Based on Hartley Transform[J]. Progress in Geophysics, 2010, 25(6): 2102-2108.

[16] 孙鹤泉,沈永明,王永学,等. Hartley变换在互相关分析中应用研究[J].大连理工大学学报，2004，44(2)：285-286. Sun Hequan, Shen Yongming, Wang Yongxue, et al. Application of Hartley Transform to Cross-Correlation Analysis[J]. Journal of Dalian University of Technology, 2004，44(2)：285-286.

[17] Bracewell R N．Discrete Hartley Transform[J]．Journal of the Optional Society of America，1983，73：1832-1835.

[18] 穆石敏，申宁华，孙运生.区域地球物理数据处理方法及其应用[M].长春：吉林科学技术出版社，1990：7-10. Mu Shimin, Shen Ninghua, Sun Yunsheng. Regional Geophysical Data Processing Method and Its Application[M]. Changchun: Jilin Science & Technology Press, 1990: 7-10.

[19] 姚长利，李宏伟，郑元满,等. 重磁位场转换计算中迭代法的综合分析与研究[J]. 地球物理学报，2012,55(6)：2062-2078. Yao Changli, Li Hongwei, Zheng Yuanman, et al. Research on Iteration Method Using in Potential Field Transformation[J]. Chinese Journal of Geophysics, 2012,55(6)：2062-2078.

[20] 马国庆，黄大年，于平，等．改进的均衡滤波器在位场数据边界识别中的应用[J]．地球物理学报，2012,55(12)：4288-4295. Ma Guoqing, Huang Danian, Yu Ping, et al. Application of Improved Balancing Filters to Edge Identification of Potential Field Data[J]. Chinese Journal of Geophysics, 2012, 55(12): 4288-4295.

Hartley Transform in the Application of the Derivatives of Potential Field (Gravity and Magnetic) Data

Ma Guoqing, Huang Danian, Du Xiaojuan, Li Lili

CollegeofGeoExplorationScienceandTechnology,JilinUniversity,Changchun130021,China

Derivative is an indispensable tool in the processing of potential field data. Now we usually use the Fourier transform to complete the computation, but this method is sensitive to noise, so cannot compute higher-order derivatives. Hartley transform (HT) is a real-valued function that is defined on the basis of Fourier transform (FT), however, symmetry character of HT is better and computational complexity of HT is smaller compared with these properties of FT. We derive the derivative computation equations of gravity and magnetic anomaly based on the basic property of HT. We demonstrate the HT on theoretical anomalies, and errors between the results computed by HT, which is insensitive to noise, and the theoretical values are less than 5%, so the HT can substitute the FT to compute the derivatives of potential field data. We also apply the HT to finish the computation of edge detection filters and obtain clearer distribution of faults.

potential field; derivative; Fourier transform; Hartley transform

10.13278/j.cnki.jjuese.201401301.

2013-06-29

国家科技专项项目(SinoProbe-09-01 201011078)；中国地质调查局地质矿产调查评价专项项目(GZH003-07-03)

马国庆(1984-)，男，讲师，博士，主要从事位场数据处理与解释方面的研究，E-mail:magq08@mails.jlu.edu.cn

杜晓娟(1957-)，女，教授，主要从事位场数据解释方面的研究，E-mail:dtdxj@jlu.edu.cn。

10.13278/j.cnki.jjuese.201401301

P631.1

A

马国庆，黄大年，杜晓娟，等.Hartley变换在位场(重、磁)异常导数计算中的应用.吉林大学学报:地球科学版,2014,44(1):328-335.

Ma Guoqing, Huang Danian, Du Xiaojuan,et al.Hartley Transform in the Application of the Derivatives of Potential Field (Gravity and Magnetic) Data.Journal of Jilin University:Earth Science Edition,2014,44(1):328-335.doi:10.13278/j.cnki.jjuese.201401301.