自适应高斯-勒让德求积法

胡松岩

西南财经大学会计学院,四川成都610074

自适应高斯-勒让德求积法

胡松岩

西南财经大学会计学院,四川成都610074

本文构造了自适应三点Gauss-Legendre求积算法，并初步对该算法和MATLAB自适应Simpson积分程序（quad函数）的计算效率进行了比较。数值结果表明:在同一精度下，该算法的计算成本大约是自适应Simpson积分算法的70%。

正交多项式;自适应Gauss-Legendre算法;自适应Simpson积分

积分是科学计算中经常遇到的问题之一。在数值积分的诸多算法中，辛普森算法是最常用的一种有效算法，许多著名的科学计算软件中计算定积分的程序都是基于辛普森算法设计的。辛普森算法的一个突出优点是在积分区间逐步细分过程中，已经计算的节点的函数值可以重复利用。与辛普森算法相比，高斯——勒让德积分法的优点是在节点数量一定的情况下具有更高的代数精度。然而，在积分区间逐步细分过程中，已经计算的节点的函数值难以重复使用。高斯积分虽然在积分计算中有诸多优点，并得到了广泛应用[1-3]，但与辛普森算法相比哪一个计算效率更高还没有见过报到。

本文，我们以三点高斯——勒让德积分法为基础，给出一种自适应数值积分算法，并与Matlab中的自适应辛普森积分法进行了数值比较。结果表明，自适应三点高斯——勒让德积分法的计算成本大约是辛普森算法的70%，计算效率明显高于辛普森积分法。

1 预备知识

1.1勒让德正交多项式

定义1.1若f( x), g( x)∈C[ a, b]，ρ(x)为[a, b]上的权函数且满足

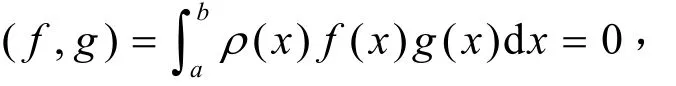
则称f( x)与g( x)在[a, b]上带权ρ(x)正交。若函数族φ0(x),φ1(x),…,φn(x ),…（有限个，或无限个）满足关系

则称｛φk(x)｝nj=0为[a, b]上带权ρ(x)的正交函数族。

定义1.2设φn(x)是[a, b]首项系数an≠0的n次多项式，ρ(x)为[a, b]上的权函数，如果多项式序列｛φk(x )｝nk=0是正交函数族，则称多项式序列｛φk(x )｝nk=0在[a, b]上带权ρ(x)正交；称φn(x)为[a, b]上带权ρ(x)的n次正交多项式。

定义1.3在区间[1,1]-上关于权函数()1xρ≡的正交多项式称为Legendre多项式。

1.2勒让德求积公式

正交多项式的根都是单实根，且分布在相应的区间内。在求积公式

中，取n+1次勒让德多项式的n+1个根作为积分节点x0,x1,…,xn，记lk(x)为拉格朗日插值基函数，即

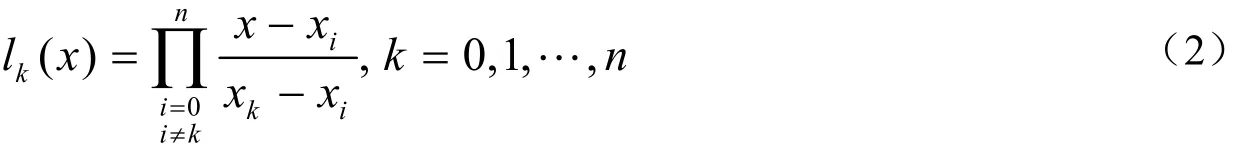
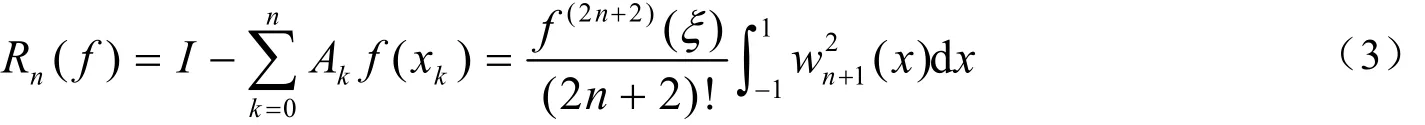
下面给出三点高斯——勒让德求积公式。

取3次勒让德多项式P3( x)=(5x3-3x)/2的三个零点作为积分节点，可得三点高斯-勒让德求积公式

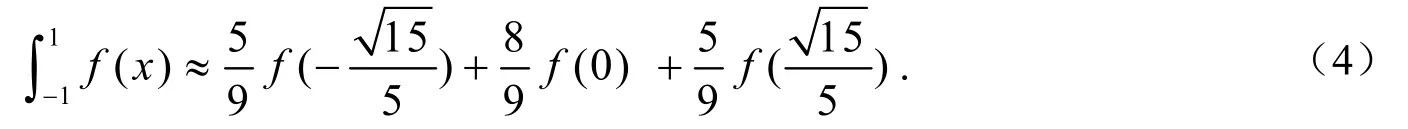
当积分区间不是[1,1]-，而是一般区间[,]a b时，只要作变换

即可得到

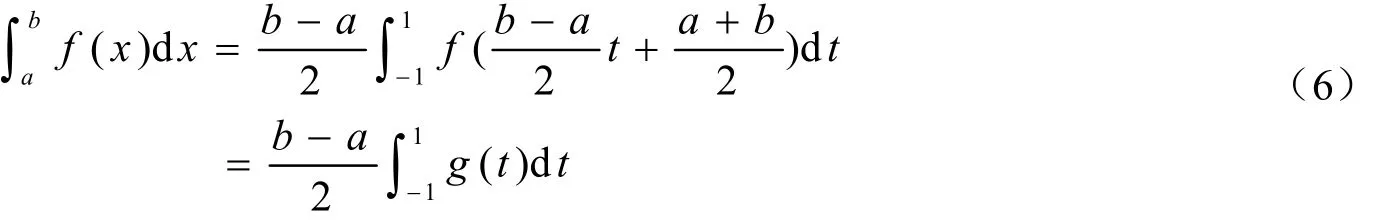
2 自适应高斯-勒让德求积法

自适应积分法就是按照积分区间上被积函数变化的剧烈程度，动态调整积分节点的分布密度，以达到节约计算成本的目的。下面三次高斯——勒让德正交多项式的根为节点，建立自适应的高斯——勒让德求积格式。

记在积分区间[a, b]的某一子区间[di, di+1]上的三点高斯-勒让德求积公式的积分值为

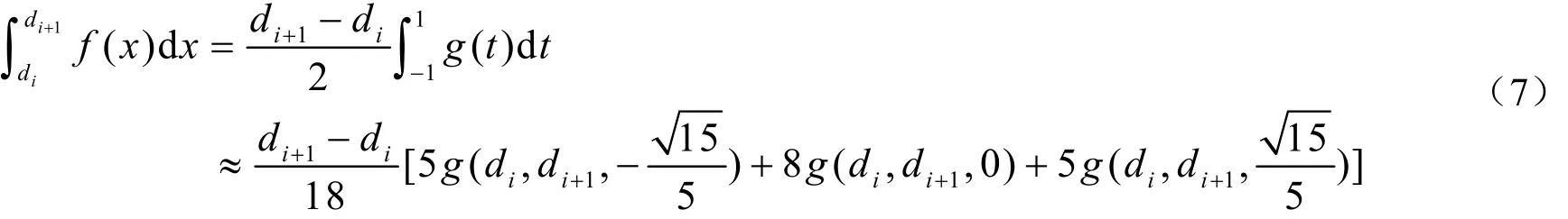
我们给出的自适应积分方法的基本思想是：整个区间[,]a b上的积分值()I f用多个子区间[di, di+1](i=0,1,…,m-1,d0=a, xm=b)上的三点高斯-勒让德积分值之和来近似，

即

假定当前区间为[c1, c2]，令

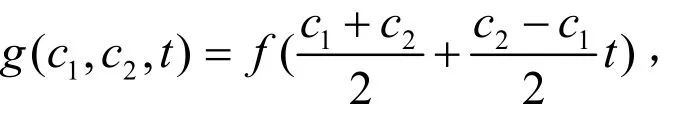
则

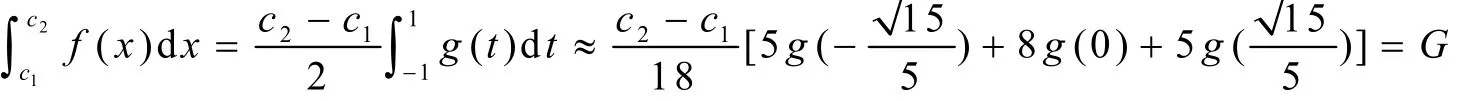
下面通过一定要求误差来判断区间是否细分，令

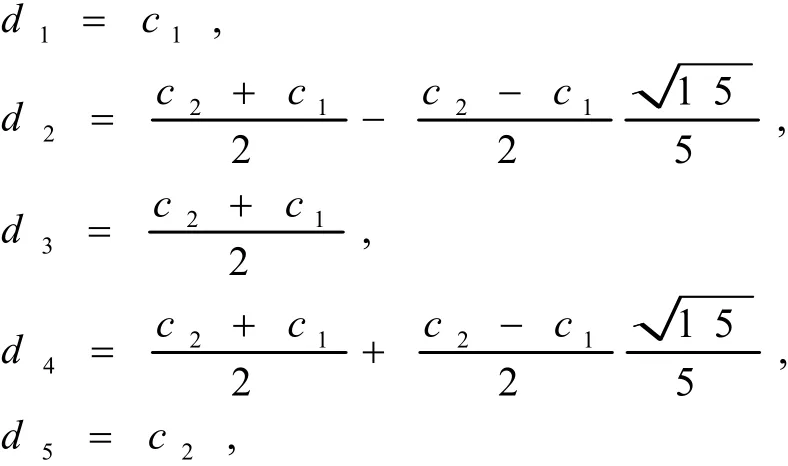
将区间[c1, c2]分成四个小区间[d1, d2],[d2,d3],[d3, d4],[d4,d5]，则

3 数值试验

我们以被积函数的原函数能够用初等函数表达的积分问题为例，通过10个算例对自适应高斯-勒让德求积算法进行了积分精确性验证.取ε=10-6，ε=10-8，采用双精度计算，与Matlab中的自适应辛普森算法的计算量进行了比较。

取ε=10-6，ε=10-8（精确解为I=-1.42602475634627），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表1。

表1 例1在两种控制精度下的计算结果Table 1 Results comparison of the two methods with different precisions on EX 1

取ε=10-6，ε=10-8（精确解为I=29.32621380439115），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表2。

表2 例2在两种控制精度下的计算结果Table 2 Results comparison of the two methods with different precisions on EX 2

取ε=10-6，ε=10-8（精确解为I=0.57079632679490），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表3。

表3 例3在两种控制精度下的计算结果Table 3 Results comparison of the two methods with different precisions on EX 3

取ε=10-6，ε=10-8（精确解为I=0.959572318005），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表4。

表4 例4在两种控制精度下的计算结果Table 4 Results comparison of the two methods with different precisions on EX 4

取ε=10-6，ε=10-8（精确解为I=0.16666666666667），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表5。

表5 例5在两种控制精度下的计算结果Table 5 Results comparison of the two methods with different precisions on EX 5

取ε=10-6，ε=10-8（精确解为I=13.28441557966756），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表6。

表6 例6在两种控制精度下的计算结果Table 6 Results comparison of the two methods with different precisions on EX 6

取ε=10-6，ε=10-8（精确解为I=315.038461538461），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表7。

表7 例7在两种控制精度下的计算结果Table 7 Results comparison of the two methods with different precisions on EX 7

取ε=10-6，ε=10-8（精确解为I=0.33333333333333），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表8。

表8 例8在两种控制精度下的计算结果Table 8 Results comparison of the two methods with different precisions on EX 8

取ε=10-6，ε=10-8（精确解为I=0.54936030677801），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表9。

表9 例9在两种控制精度下的计算结果Table 9 Results comparison of the two methods with different precisions on EX 9

取ε=10-6，ε=10-8（精确解为I=0.27219826128795），利用自适应三点高斯勒让德算法以及自适应辛普森算法分别计算积分，计算结果见表10。

表10 例10在两种控制精度下的计算结果Table 10 Results comparison of the two methods with different precisions on EX 10

4 结论与讨论

本文基于三点高斯-勒让德求积公式构造了一种自适应积分算法。根据我们的数值试验，当计算精度为ε=10-6时，三点自适应高斯-勒让德求积算法的平均计算量约为辛普森算法的71%；当计算精度为ε=10-8时，三点自适应高斯-勒让德求积算法的平均计算量约为自适应辛普森算法的65%，由此可见新算法具有一定的实用价值。根据我们的数值经验，两点自适应高斯-勒让德求积算法的计算效率远比三点的算法低，甚至不如自适应辛普森算法，而四点及以上的自适应高斯-勒让德求积算法将显著增加子区间的分割数量，从而降低计算效率。因此，我们认为，三点自适应高斯-勒让德求积算法在该类算法中，应该是最好的。

[1]李炯城,林惜斌,肖恒辉,等.高阶高斯型积分计算机求解算法[J].计算机工程与设计,2012,33(5):1871-1875

[2]张庆礼,王晓梅,殷绍唐,等.高阶高斯积分节点的高精度数值计算[J].中国工程科学,2008,10(2):35-40

[3]周立峰,吴明.用高斯积分法计算混油浓度[J].天然气与石油,2005,23(5):4-6

Self-adaptive Gauss-Legendre Quadrature Method

HU Song-yan
School of Accounting,Southwestern University of Finance and Economics,Chengdu610074,China

In this paper,a self-adaptive three point Gauss-Legendre quadrature method was proposed and the efficiency of the method was compared with the program of QUAD in MATLAB preliminarily.In view of function evaluation times,the computation cost of the new method was almost 70 percentage of QUAD under the same precision.

Orthogonal polynomials;self-adaptive Gauss-Legendre quadrature method;self-adaptive Simpson-method

O241.4

A

1000-2324(2014)04-0610-05

2013-03-11

2013-03-20

胡松岩(1992-),女,汉族,山东栖霞人,本科生.