城市轨道交通客流预测算法设计与仿真
高慧昀,李少伟
城市轨道交通客流预测算法设计与仿真
高慧昀1,李少伟2
1.毕节学院物理科学与技术学院,贵州毕节551700
2.同济大学电子与信息工程学院,上海201804
为了实现对城市轨道交通的客流预测,提出了一种混合神经网络及卡尔曼滤波器的客流数据预测算法.算法分为两步:基于神经网络的客流预测以及基于卡尔曼滤波器的数据修正。选择ELMAN神经网络作为客流预测工具,在网络输出计算结果后,根据统计数据,采用卡尔曼滤波器对输出数据进行修正,以实现对预测结果精度的提高。为验证模型正确性,选择上海地铁作为研究对象,进行了系统仿真。实验结果表明,上述混合算法比单纯其中一种算法具有更小的误差以及更好的实际效果。
轨道交通;客流预测;ELMAN神经网络;卡尔曼滤波器;系统仿真
随着我国城市化建设的不断加快,大量人口涌入城市,特别是北京、上海、广州等特大城市人口增长迅速.在这些城市中,由于经济比较发达,机动车保有量已大大超出城市道路能够承受的容量。这种情况带来的最直接后果就是交通堵塞,出行成本上升,资源浪费严重.而轨道交通因其具有运量大(4~6万人次/h)、单位运量资源消耗少(采用电气化方式驱动)、运行准点率高(拥有独立的运行轨道)等优势,已然成为了解决大城市交通问题最理想最有效的方法.越来越多的城市居民也逐渐将轨道交通作为出行的首要交通工具[1]。
为了满足大量乘客的出行需求,轨道交通系统需要制定一套高效的调度策略,而轨道交通的客流量,可以说就是决定轨道交通调度策略的最主要因素[2]。为了最大限度发挥轨道交通的运行优势,设计一种尽可能精确的客流预测算法,并以此算法作为指导,优化轨道交通调度策略,有着深远的现实意义。
由于客流预测算法直接影响着轨道交通的运行效率,相关研究人员都在此领域进行了大量的研究,并采用不同的算法,建立了相应的模型进行了实现。
吕慎,过秀成提出了一种基于四阶段法改进的轨道交通客流预测方法[3]。这种方法主要运用管理学手段对轨道交通客流进行分析,从宏观角度考虑了客流的分布;Zhang Dongquan采用BP神经网络对轨道交通客流进行预测[4];鲁明旭,叶银忠,马向华将ELMAN神经网络应用到轨道交通客流预测中,预测精度较传统BP神经网络有所提高,平均误差较传统BP神经网络预测算法提高了约2个百分点[5];陈大伟,肖为周,李旭宏等人提出了基于迭代反馈约束的城市轨道交通客流预测模型框架,并以改进的四阶段法作为模型框架算法[6]。
由于轨道交通客流组成比较复杂,以上模型在预测算法以及精度方面并未达到较高的可信度,主要表现:1.缺乏有效的实验数据或实验数据不够完整,仅仅在理论上提出了算法的结构与框架;2.理论与实验之间有脱节的感觉,无法获知理论支撑是如何应用到实验中的,实验结果无法令人信服。
为了提高轨道交通客流的预测精度,满足实际需求,本文在参考已有算法的基础上,提出了一种基于混合ELMAN神经网络和卡尔曼滤波器的客流预测算法[7].文章在建立了算法框架模型,并详细给出了算法中各参数的确定方法后,以上海市轨道交通客流作为研究对象,对模型进行了验证,给出了具体的实验步骤.实验结果表明,相对于已有算法,本算法模型在客流预测精度方面有一定的提高。
1 神经网络模型建立
神经网络是一种大规模并行分布处理的非线性系统,具有高度的非线性运算能力和的自学习、自组织、联想记忆和并行处理能力,神经网络的信息分布式存储在权系数中,具有集体运算和自适应学习的能力。由于轨道交通客流是一个非平稳随机过程,且客流量相对时间具有非线性特性,故采用神经网络算法能够较好的处理客流预测这类问题[8,9]。
1.1ELMAN神经网络模型
ELMAN神经网络模型在普通前馈网络的隐藏层中增加一个承接层,作为一步延时算子,以达到记忆的目的,从而使系统具有适应时变特性的能力,能直接反映动态过程系统的特性。如图1所示为ELMAN神经网络结构,从图中可以看出,ELMAN神经网络在输入层多出了承接层,其输入与隐藏层神经元的输出相关。

图1 ELMAN神经网络结构Fig.1 ELMAN neural network structure
ELMAN神经网络的运算规则由以下四个等式组成

其中X(k)为网络的输入为,Y(k)为网络输出,Wi,i+1为连接第i层与第i+1层神经元的权值矩阵,Bi为第i层神经元的偏置输入为,C(k)为承接层的输入,Hi(k)、Ho(k)分别为隐藏层的输入输出.等式(1)中的[C(k),X(k)]表示连接向量C(k)与向量X(k)。
1.2神经网络训练
反向传播算法(Back-Propagation Algorithm)具有算法简单、运算速度快等特点,是神经网络训练中最常用的算法。采用BP算法进行神经网络训练,需要用到如下信息

I.输入的前向传播

II.反向传播
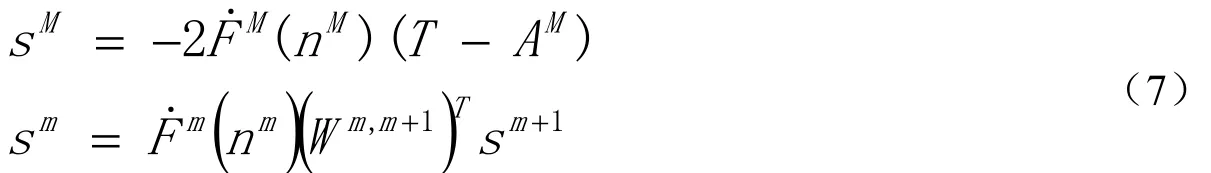
III.权值和偏置值的更新

其中

η表示学习率,它可以是一个常数,也可以按一定的规则,在每次样本训练中取不同的值。
需要注意的是,由于权值矩阵初值的选择可能造成神经网络最终收敛的局部最小点可能并非是全局最小点。
1.3训练样本选取
为了对神经网络进行有监督的训练,必须要选定训练样本的输入与输出。训练样本的输入即影响轨道交通客流的各种外部环境因素;样本的输出为轨道交通客流的观测值。表1详细列出了本算法选取的神经网络输入样本,包括天气因素、国家政策、重大节假日等等;同时,为了方便神经网络和计算机对上述各项信息的处理,在将上述信息作为训练样本输入到神经网络以前,对其进行了数字化处理,如表1第二列所示。

表1 影响轨道交通客流分布的若干关键因素及数字化结果Table 1 Influence the distribution of rail transit passenger flow and some key factors and the digital results
2 卡尔曼滤波器
卡尔曼滤波器是一种由卡尔曼(Kalman)提出的用于时变线性系统的递归滤波器。在本算法中,我们应用卡尔曼滤波器对神经网络的输出结果进行修正,使得预测结果更加精确[10]。
2.1卡尔曼滤波器模型
卡尔曼滤波器由预测及更新方程组组成


其中方程组(10)(11)为预测方程组,方程组(12)(13)(14)为更新方程组;A是作用在xk-1上的状态变换模型;B是作用在控制器向量uk上的输入—控制模型;Q是过程噪声协方差矩阵,Rk是观测噪声协方差矩阵。
卡尔曼滤波器模型详细推导过程以及各参数的详细意义可以参考文献[10]。
2.2卡尔曼滤波器参数构造
2.2.1 观测噪声方差卡尔曼滤波器假设观测噪声满足高斯分布,如下式所列:

对观测噪声方差的求解,可以很自然的认为是对高斯分布中未知参数进行估计。根据概率论的基本知识,采用最大似然估计法来对分布函数中的未知量进行估计。
高斯分布的最大似然函数为

为了便于算法的求解,将最大似然函数转换为对数最大似然函数

对等式(17)求一阶及二阶微分,令等式为零,计算极值点

求解方程组(18)(19),得到高斯分布最大似然估计值

由于观测噪声分布函数均值为零,在此令Oi表示第i日客流统计数据,Pi表示第i日的预测客流数据,以客流预测误差作为分布函数的均值,即

将式(22)(23)代入式(21)中,可计算得到观测噪声分布函数方差.需要注意的是,按上述方法求出的方差并非一个常数,而是随着新的统计数据不断的加入,呈现出相应的变化。
2.2.2 其他参数的确定n天内,轨道交通的观测客流量与预测客流量比例的期望为

增益A可采用如下形式表示

A的值随着观测数据的加入,呈现动态变化。
记P0为误差估计协方差P的初值,其取值通常并不关键,因为几乎任何P0≠0都会使滤波器最终收敛。在这里我们令P0=1。
由于轨道交通的日客流量统计由机器直接完成,其统计误差可由观察数据得到。通常情况下,我们认为客流统计误差接近于零,可以忽略不计。在此我们直接将过程激励噪声的方差Q设定为零。
2.3混合神经网络及卡尔曼滤波器的客流数据预测算法
图2为混合神经网络及卡尔曼滤波器的训练信号流图,包括如下几个步骤:
(1)一个输入训练模式ku沿网络传播得到输出向量ky⌒,同时计算误差向量kμ;
(2)微分矩阵kH通过反向传播获得,对于输出向量ky⌒的每一个分量,都有一个独立的反传过程;
(3)卡尔曼增益矩阵kK将作为微分矩阵kH、逼近误差方差阵kP和量噪声方差阵kR的一个函数来计算,这一步还包括全局规范矩阵kA的计算;
(5)逼近误差方差阵1kP+可以利用卡尔曼增益矩阵kK、微分矩阵kH和当前逼近误差方差阵kP及过程噪声方差阵kQ来更新。
3 模型仿真实验
为了验证模型算法的正确性与实用性,我们选择上海轨道交通作为研究对象。首先,将轨道交通的历史统计数据作为训练样本输入到神经网络,使得网络具有客流预测能力;然后,用神经网络预测一段时间内的客流数据,并应用卡尔曼滤波器对预测结果进行修正;最后,计算预测数据与实际数据之间的误差,并量化预测精度。
3.1输入样本数据
在本次样本数据中,我们选取了2012年7、8、9、10月,共计123 d的样本数据。在这四个月中,刚好涵盖了季节的变迁、重大节假日以及汽油价格波动等情况,这样可以便于网络对各种环境的适应.在横跨4个月的时间内,部分数据由于官方渠道未有发布,算法在处理时,直接采取丢弃样本的策略,以保证算法能够正常进行,有效样本数量为117个。
按照表1所述方法,以各种环境因素,包括:天气、日期、星期、经济环境等等作为神经网络训练样本的输入,并对输入样本做数字化处理,最终形成神经网络的训练样本的输入。

图2 混合神经网络及卡尔曼滤波器的训练信号流图Fig.2 The signal flow graph of Hybrid ELMAN neural network structure and Kalman filter
3.2输出样本数据
如图3用实线所标示曲线为采样时间内的客流走势图。从图中可以明显看到轨道交通客流的几个特征:1.客流量大体呈现出以一周为一个循环周期;2.随着时间的推移,客流量有一种上升趋势。这是由于城市的发展、汽油价格的上升等因素,导致了更多的市民选择乘坐轨道交通出行。3.9月29日的客流呈现出明显的下降现象,这是由于10月1日为国定长假的原因,从另一方面也正好说明了重大节假日对轨道交通的客流的影响。
3.3模型仿真
利用Matlab工具箱中的函数对ELMAN神经网络进行建模仿真[11,12]。选取学习率可变的动量BP算法,设定不同的参数对网络进行训练,训练结果如下表所示。

表2 训练结果Table 2 Training results
从表2中可以看到,隐藏神经元的数目会对运行时间造成较大的影响,而过多的隐藏神经元反而会造成误差的增加。根据表中的数据,我们选取第四行数据作为神经网络的训练参数。如下图3所示为神经网络训练完毕后,对历史客流数据的拟合。
接下来我们选取上海轨道交通2012年11月1日至11月5日的客流作为预测对象,对ELMAN神经网络预测模型进行检验,得到图4所示的结果。

图3 客流数据拟合Fig.3 passenger data fitting

图4 预测结果Fig.4 Predictions
3.4误差修正
将神经网络预测得到的数据通过卡尔曼滤波器进行修正,修正算法已在第2部分详细介绍,数据修正结果如下表所示。
从表3可以看到,经过卡尔曼滤波器修正后,预测数据与真实数据之间的误差有所减少。同时可以看到,卡尔曼滤波器方差P在计算过程中不断向零趋近,这也验证了其初值的选取并不会影响滤波器的计算。在表4中列出了神经网络预测误差与卡尔曼滤波器修正后的误差对比。

表3 数据修正Table 3 Data correction
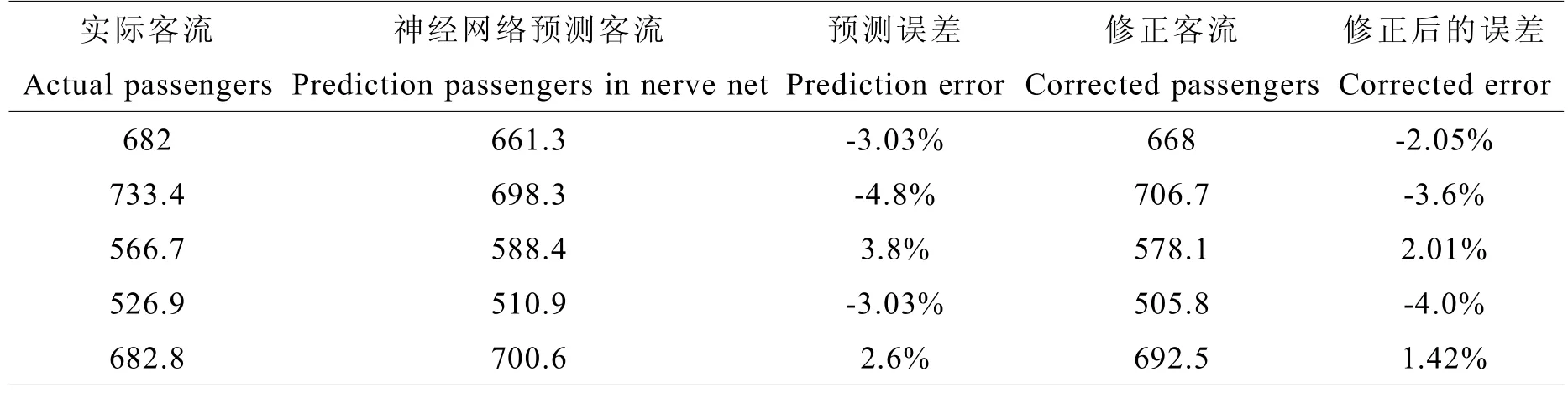
表4 误差对比Table 4 Comparison error
4 实验结论
从实验中我们可以看到,单纯采用神经网络算法对轨道交通客流进行预测,最大绝对误差为4.8%,经过卡尔曼滤波器修正后,最大绝对误差减小到4.0%。这是由于卡尔曼滤波器会将历史误差信息加入到计算中,从而实现预测精度的提高。
在下一步的研究中,主要可以围绕以下目标展开:1.为了进一步提高神经网络的预测精度,神经网络的训练样本应覆盖更多的情况,也就是说,神经网络需要更大的训练样本;2.由于轨道交通各站点客流数量不均衡,可以对单独站点的客流进行预测,以实现对特定站点的管理。
[1]黄树森,宋瑞,陶媛.大城市居民出行方式选择行为及影响因素研究-以北京为例[J].交通标准化,2008,9:124-128
[2]Shaowei Li,Yongsheng Chen.Dynamic schedule strategy for urban rail transit[J].International Journal of Digital Content Technology and its Applications,2012,6(3):86-92
[3]吕慎,过秀成.轨道线网客流预测方法研究[J].系统工程理论与实践,2001,8:106-110
[4]Zhang Dongquan.Passenger Flow Forecast of Urban Rail Transit Based on BP Neural Networks[C]//Intelligent Systems andApplications.Qingdao:IEEE,2011:1-4
[5]鲁明旭,叶银忠,马向华.神经网络在地铁客流预测中的应用[J].机械研究与应用,2012,3:86-89
[6]陈大伟,肖为周,李旭宏等.迭代反馈约束下的城市轨道交通客流预测分析[J].华南理工大学学报(自然科学版),2011,39(8):99-103
[7]张余生,夏秀渝,杨莎.基于神经网络和卡尔曼滤波算法的说话人识别[J].成都信息工程学院学报,2008,23(4):384-388
[8]Simon Haykin.Neural Networks Principle:2nd Edition[M].Beijing:China Machine Press,2004
[9]Martin T.Hagan.Design Neural Network[M].Beijing:China Machine Press,2002
[10]Greg Welch,Gary Bishop.An Introduction to the Kalman Filter[R].Carolina:Department of Computer Science University of North Carolina,2006
[11]Duane Hanselman.Bruce Littlefield.Mastering Matlab 7[M].Beijing:Tsinghua University Press,2006
[12]葛哲学,孙志强.神经网络理论与MATLAB R2007实现[M].北京:电子工业出版社,2007
Design and Simulation of Passenger Flow ForecastAlgorithm for Urban Rail Traffic
GAO Hui-yun1,LI Shao-wei2
1.Physical Science and Technology School,Bijie College,Guizhou551700,China
2.School of Electronics and Information,Tongji University,Shanghai201804,China
A kind of passenger flow forecast algorithm for urban rail traffic was proposed.It was composed by ELMAN neural network and Kalman filter.The network configured out the result of passenger amount,and then,in order to enhance the data precision,the outcome was revised according to the statistical error through Kalman filter.Eventually,the model was verified with Shanghai metro as a sample.Experimental results showed that the hybrid algorithm had the practical effect of a smaller error and better than one of simply single algorithm.
Rail traffic;passenger flow forecast;ELMAN neural network;Kalman filter;system simulation
U492.4+13
A
1000-2324(2014)04-0588-07
2012-07-01
2012-11-20
国家科技支撑计划(2009BAG18B04)
高慧昀(1980-),男,山西保德,汉,硕士,讲师,主要研究方向为理论物理智、电子信息技术在交通等领域的应用.E-Mail:lgownr@163.com.

