LY12铝合金在冲击绝热压缩下的泊松比

谭华,俞宇颖,戴诚达,谭叶

(中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室,四川绵阳 621900)

LY12铝合金在冲击绝热压缩下的泊松比

谭华,俞宇颖,戴诚达,谭叶

(中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室,四川绵阳 621900)

对泊松比的意义进行讨论,给出了单轴应变加载下线弹性区的泊松比与纵向应力和横向应力的关系,以及准弹性区的泊松比与声速的关系。通过实验测量LY12铝合金在冲击压缩下的纵波和体波声速,计算在20～131 GPa冲击压力范围内的泊松比。实验结果表明:LY12铝合金在发生冲击熔化前泊松比基本保持为常数,约为0.32左右;发生冲击熔化后混合相区的泊松比快速增加;当接近完全熔化时泊松比趋于理论极限值0.5.泊松比测量为确定金属的冲击熔化压力区间提供了一种有用的方法。

固体力学;泊松比;声速;单轴应变;准弹性;冲击熔化

0 引言

在单轴应变加载下,现有实验技术能够对纵向应力和应变进行精确测量,但是依然难以对横向应力进行直接测量。虽然在低应力加载下可以用锰铜计测量横向应力,但是横向计的精确标定相当困难。由于应力计衬垫材料的影响和实验安装问题,特别是安装横向锰铜计的缝隙方向与冲击波的传播方向平行,缝隙中的填充材料在纵向冲击应力作用下产生的应力扰动会对横向锰铜计产生附加的干扰[1],影响横向应力测量,导致横向应力实测数据发生异常并常常受到各种质疑。本文推导了在单轴应变加载下线弹性区材料横向应力与泊松比的关系。因此,只要能够设法测量单轴应变加载下线弹性区的泊松比,就可以利用泊松比计算线弹性变形下的横向应力,对不同填充材料对横向锰铜计测量及标定的影响开展研究。

另一方面,基于纵向模量、体积模量和剪切模量与泊松比之间的一般性关系,以及单轴应变加载下的模量与纵波、体波或横波声速的关系,可以将泊松比与声速直接联系起来。经过近些年的发展,我们能够比较精确地测量沿着Hugoniot线的声速,以及从Hugoniot状态卸载时沿着准弹性卸载路径的声速[1-2],使实验测量和研究沿着冲击绝热线的泊松比成为可能。

1 基本模型

1.1 线弹性变形下的泊松比与纵向应力和横向应力的关系

在力学中,泊松比是用单轴应力弹性变形条件下的横向应变εy与纵向应变εx之比来定义的[3],

取压缩应变为正,拉伸应变为负,以保证泊松比具有正值。在泊松比的直观定义中,杆的边侧(横向)处于自由应力状态(如图1所示),纵向应变和横向应变均是由纵向应力σx引起的。利用自由边侧条件下纵向弹性压缩模量即杨氏模量E的定义,可将材料的横向应变εy表示为

图1 泊松比的定义Fig.1 A sketch of the definition of Poisson's ratio

在单轴应变实验中,材料处于三轴应力作用下且横向应变等于0.显然不能直接根据(1)式计算单轴应变下的泊松比。在单轴应变线弹性变形条件下,假设施加于横向(y方向)的应力为σy,则它在x方向产生附加的纵向弹性应变ε′x,

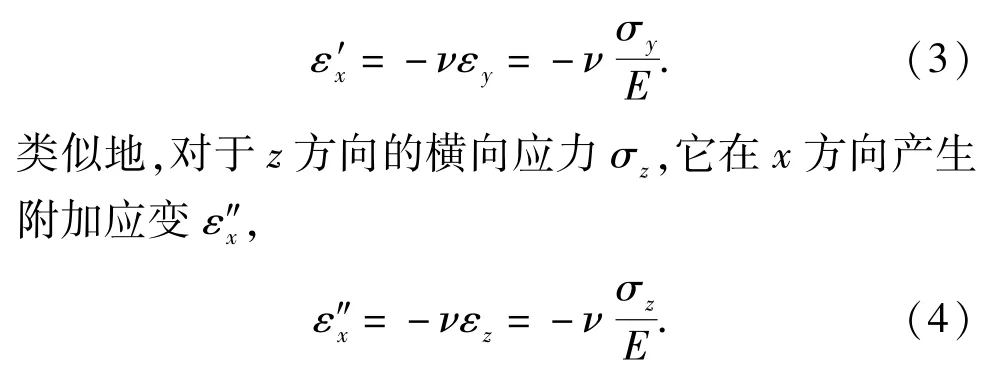
因此三轴应力加载线弹性变形条件下x轴方向的总弹性应变等于上述应变的代数叠加,即

(8)式给出了单轴应变线弹性变形下的纵向应力与横向应力及泊松比的关系。这样,只要能够同时测量泊松比和纵向应力σx,就可以知道横向应力σy,这为研究单轴应变条件下线弹性材料的横向应力提供了一种方法。

1.2 单轴应变加载下的泊松比与声速

众所周知,平面单轴应变加载下的纵向应力σx与平均应力及纵向偏应力S可表示为

对于各向同性材料,平均应力为(σx+2σy)/3=p,偏应力为2(σx-σy)/3.按照声速的定义,即小扰动应力波的传播速度[4]。这种小扰动应力波既可以是等熵的,也可以是非等熵的,即准等熵的。在小扰动应力作用下,最大剪应变γ与纵向应变εx相等[3]:γ=εx.根据(9)式容易得到一维应变加载下的纵波声速cl与体波声速cb和横波声速ct的普遍性关系,

式中:最大分解剪应力 τ=τmax=(σx-σy)/2=3S/4.根据体积模量、剪切模量与杨氏模量和泊松比的一般性关系[3]:

因此,只要能够测量精确声速,就能确定泊松比。显然,当固体材料发生完全熔化处于液相状态时,材料失去抗剪能力:τ=0,因此G=0或ct=0.或者处于弹-塑性屈服转变状态时,剪应力达到极值:τ=τmax,因此也有G=0或ct=0成立。在这两种情况下均有ν=1/2,这就是泊松比极限值。

在强冲击压缩下,只要材料不处于完全冲击熔化状态,从冲击压缩状态卸载时或受到再加载时金属材料将表现出弹-塑性转变,这种弹性称为准弹性。Yu等[2]的实验结果表明,沿着准弹性卸载路径,剪切模量和体积模量并不保持为常数,线弹性变形假设在准弹性区不再成立。因此准弹性下的应力-应变关系及变形特性不能用线弹性关系来描述。也就是说(8)式在准弹性区不成立。但(17)式及(18)式是从一般的弹性力学关系推导出来的,因此依然能够通过声速测量计算准弹性状态下的剪切模量和泊松比。

(10)式中的声速是热力学声速或欧拉声速,从一维应变实验测量到的声速是拉氏声速。拉氏声速a与欧拉声速c的关系[4-5]为

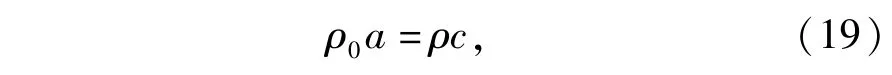
式中:ρ0表示初始态密度。(17)式和(18)式用拉氏声速可表示为

总之,声速测量为我们提供了一种确定准弹性区的泊松比的重要方法。由于Hugoniot状态是卸载路径的起始点,因此(17)式～(21)式也可用来计算沿着冲击绝热线的泊松比。

1.3 Hugoniot弹性极限下的泊松比及屈服强度

Hugoniot弹性极限被定义为材料在冲击加载下发生弹-塑性屈服的起始应力。在理想弹性-塑性模型假设下,并忽略弹性变形到塑性变形的转变过程,若达到Hugoniot弹性极限σHEL时材料的应变为εHEL,则对应的流体静水压p=KεHEL.假定上、下屈服面以流体静水压线对称,则屈服强度Y与σHEL及流体静水压强p之间的关系为

在冲击加载实验中,通过多台阶样品实验测量获得粒子速度剖面并判定Hugoniot弹性极限对应的粒子速度uHEL,结合拉氏声速aHEL计算Hugoniot弹性极限为

根据Hugoniot弹性的定义,此时材料的应力状态恰好位于上屈服面,由屈服强度的定义,结合(8)式得到Hugoniot弹性极限时的屈服强度为

2 LY12铝合金沿着Huogoniot的泊松比实验测量

在高达数十至数百吉帕冲击加载下,处于固相区的金属材料依然会表现出某种弹性特征,这种弹性称为“准弹性”。它表明Hugoniot状态不一定在屈服面上。然而金属材料在高压冲击加载下发生了弹-塑性屈服也是不争的事实,二者之间似乎存在“矛盾”。

强冲击加载应力波的前沿可达亚纳秒甚至皮秒量级,应变率高达109s-1甚至更高,这种极端应力-应变率过程发生在冲击波阵面上;但冲击波加载的终态即Hugoniot状态是热力学平衡态,其应变率接近于0.从冲击波阵面到波后Hugoniot状态,应变率发生了急剧改变。应变率的急速改变导致剪应力的松弛[6],这可能是导致Hugoniot状态偏离屈服面的主要原因。由此看来,用横向应力计测量的Hugoniot状态下的横向应力并不代表在冲击压缩屈服面上的横向应力,或者说根据锰铜计测得的横向应力计算的纵向应力与横向应力之差,并不能代表冲击加载下材料的屈服强度。

图2给出了Yu等[2]测量的国产商用LY12铝在20～100 GPa压力范围内6个Hugoniot压力点(LY1～LY6)下的拉氏纵波声速与粒子速度的关系,以及从冲击压缩状态卸载时声速随粒子速度的变化。实验中利用中国工程物理研究院流体物理研究所的二级轻气炮驱动铝飞片到高速撞击铝样品产生强冲击压缩;用VISAR激光速度干涉仪或DISAR位移干涉仪测量铝样品与LiF窗口的界面粒子速度剖面。根据粒子速度剖面计算铝样品在冲击加载下和沿着卸载路径的声速[2,4]。这 6个数据点的Hugoniot状态列于表1中。图3中对高于100 GPa的冲击压力点,用钽飞片进行非对称碰撞实验,声速的计算方法见文献[2,4],最高压力点为131 GPa,已经进入铝的冲击熔化固液混合相区。

图2 实验测量的LY12铝沿着Hugoniot的拉氏声速以及从冲击压缩状态卸载时沿着准弹性-塑形卸载路径的拉氏声速随粒子速度的变化Fig.2 The measured Lagrange sound velocities of LY12 Al alloy materials along the Hugoniot and the change of Lagrange sound velocity with particle velocity along the quasi elastic-plastic release path

由于缺乏LY12铝的零压声速数据,表中列出了2024铝合金和6061铝合金的零压声速数据供参考。根据声速数据利用(21)式计算了LY12铝合金在冲击压缩下的泊松比νH,列于表1的最后一列。从20～100 GPa范围内6发对称碰撞实验的结果来看,这一压力范围内LY12铝在冲击压缩下的泊松比基本保持常数,其平均值约等于0.32,如图3的虚线所示。

表1 LY12铝合金沿着冲击绝热线的声速测量结果与泊松比Tab.1 Measured sound velocities along the Hugoniot and the corresponding Poisson's ratio

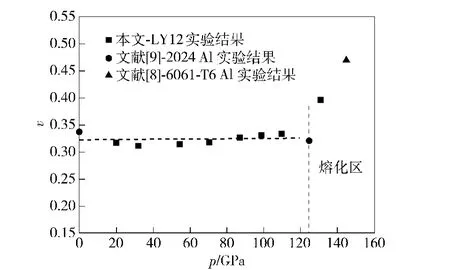
图3 铝的泊松比随加载压力的变化Fig.3 Poisson's ratios of LY12 alloy materials vs.shock pressures

3 讨论

Reinhart等测量了6061-T6铝的声速并报道了根据声速计算了泊松比[8]。他们的结果表明,6061-T6铝合金在43～115 GPa冲击压力范围内的泊松比的变化很小,约为0.33,与本文的结果非常接近。Brown等用光分析法测量了钽在约150～400 GPa压力区的声速[10]。在钽发生冲击熔化(约300 GPa)前的固相区,他们假定们泊松比与冲击压力的关系计算得到的纵波声速随压力的变化与他们的实验测量结果符合。考虑到光分析法本身的不确定度,实际也可以认为固相区的泊松比近似为常数。

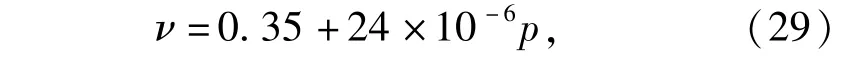
沿着冲击绝热线的体波声速易于根据实测冲击绝热线数据和Gruneisen物态方程计算得到[2,4],而横波声速测量较困难。冲击压缩下金属材料在固相区的泊松比基本保持为常数这一事实,为利用泊松比和Hugoniot数据估算冲击高压下的纵波和横波声速提供了极大方便。根据实测的和泊松比和Hugoniot弹性极限可以直接计算Hugoniot弹性极限时的屈服强度YHEL.文献[9]给出了2024铝的实测值σHEL=0.6 GPa及YHEL=0.29 GPa,按照ν=0.33用(28)式计算得到2024铝在Hugoniot弹性极限时的屈服强度为0.30 GPa,与实验测量结果十分接近。

铝在125 GPa冲击加载下发生冲击熔化。表1中列出了McQueen利用光分析法测量的125 GPa压力下的纵波声速[9],以及本文根据铝的冲击绝热线和Gruneisen物态方程计算的在125 GPa压力点的体波声速,据此计算的泊松比也列于表1和图3.根据Yu等[2]测量的LY12铝在131 GPa冲击加载下的粒子速度波剖面的结构,虽然已经进入铝的冲击熔化固液混合相区,但从波剖面依然可以观察到显著的准弹性-塑性卸载特征,并非像通常认为的那样一旦发生冲击熔化材料就进入流体状态不存在弹-塑性卸载特征。这表明即使发生了冲击熔化,只要熔化没有完成,材料依然具有一定的强度。根据实测波剖面计算了LY12铝的纵波和体波声速,得到131 GPa下的泊松比约为0.4,说明部分冲击熔化使LY12铝的泊松比迅速增加。泊松比的增大意味着横波声速下降,导致材料的剪切模量减小,意味着材料抵抗剪切加载能力的下降。泊松比的这一特性为判定金属的冲击熔化提供了一种方法。有趣的是,Reinhart等在研究6061-T6铝合金的强度特性时也发现了类似的结果[8]。他们根据6061-T6铝在145 GPa的纵波和体波声速计算得到泊松比为0.47,而6061铝发生完全冲击熔化时压力大约在160 GPa左右,此时根据声速计算的泊松比达到了0.5.因此,声速测量和泊松比为我们提供了一种确定从起始冲击熔化到完全冲击熔化的压力区间的有用方法。

4 小结

本文从泊松比的定义出发,推导了在单轴应变加载条件下的泊松比与纵波声速、横波声速及体波声速之间的关系;将泊松比的应用范围从经典的单轴应力弹性加载状态拓展到了单轴应变弹性和和准弹性加载状态。

根据实验测量在 20～131 GPa冲击压缩下LY12铝合金的纵波和体波声速,计算了LY12铝合金的泊松比,并与国外类似的研究结果进行了比较。发现LY12铝合金的泊松比在固相区基本保持为常数0.32,与国外同类铝合金的结果非常接近;在发生冲击熔化后,在固-液混合相区LY12铝合金的泊松比随冲击压力迅速增加;发生完全熔化后泊松比趋于理论极限值0.5.

泊松比研究为根据物态方程给出的体波声速计算沿着冲击绝热线的纵波声速和横波声速提供了方法,也提供了一种确定从起始冲击熔化到完全冲击熔化的压力区间有用方法。

References)

[1] Kanel G I,Razorenov S V,Fortov V E.Shock-wave phenomena and the properties of condensed matter[M].NY:Springer-Verlag New York Inc,2004.

[2] Yu Y Y,Tan H,Hu J,et al.Determination of effective shear modulus of shock-compressed LY12 Al from particle velocity profile measurements[J].Journal of Applied Physics,2008,103: 103529.

[3] 杨桂通.弹塑性力学引论[M].北京:清华大学出版社,2000.

YANG Gui-tong.Introduction to elastic-plastic mechanics[M]. Beijing:Tsinghua University Press,2000.(in Chinese)

[4] 谭华.实验冲击波物理导引[M].北京:国防工业出版社, 2007.

TAN Hua.Introduction to experimental shock-eave physics[M]. Beijing:National Defense Industry Press,2007.(in Chinese)

[5] 谭华.拉氏坐标与守恒方程[J].高能量密度物理,2012(1): 5-10.

TAN Hua.Lagrangian coordinate and the conservation laws[J]. High Energy Density Phyics,2012(1):5-10.(in Chinese)

[6] Bringa E M,Caro A,Wang Y M,et al.Ultrahigh strength in nanocrystalline materials under shock loading[J].Science.2005, 309(5742):1838-1841.

[7] Marsh S P.Shock L.Hugoniot data[M].Berkley,CA:University of California Press,1980.

[8] Reinhart W D,Asay J R,Chhabildas C,et al.Investigation of 6061-T6 aluminum strength properties to 160 GPa[J].AIP Conference Proceedings,2009,1195:977-980.

[9] McQueen R G,Hopson J W,Fritz J N.Optical technique for determining rarefaction wave velocities in very high pressure[J].Review of Scientific Instruments,1982,53(2):245.

[10] Brown J M,Shaner J W.Rarefaction velocities in shocked Tantalum and the high pressure melting point[M]∥Asay J R,Graham R A,Straub G K.Shock Waves in Condensed Matter-1983.Amsterdam,Holland:North Holland Physics Publishing,1984: 91-94.

Poisson's Ratio of LY12 Aluminum Alloy under Shock Compression

TAN Hua,YU Yu-ying,DAI Cheng-da,TAN Ye
(National Key Laboratory of Shock Wave and Detonation Physics,Institute of Fluid Physics, China Academy of Engineering Physics,Mianyang 621900,Sichuan,China)

The physical meaning of Poisson's ratio is discussed.The relationships among the Poisson's ratio and the longitudinal and transverse stresses under uniaxial strain shock loadings,and the relationship between the Poisson's ratio and the sound velocity in quasi-elastic deformation region are presented. Poisson's ratios of LY12 aluminum alloy materials are calculated based on the sound velocities measured at shock pressures from 20 GPa to 131 GPa.It is found that,while the Poisson's ratios keep almost constant,i.e.,0.32,before shock-melting happens,it increases rapidly in the shock-melting solid-liquid mixed phase region and approachs the theoretical limit of Poisson's ratio,i.e.,0.5,as shock-melting completes,which may provide us a useful way for identifying the shock induced melting zone.

solid mechanics;Poisson's ratio;sound velocity;uniaxial strain;quasi-elasticity;shockinduced melting

O347.5

:A

:1000-1093(2014)08-1218-05

10.3969/j.issn.1000-1093.2014.08.013

2013-08-20

国家自然科学基金项目(10972206)

谭华(1942—),男,研究员,博士生导师。E-mail:zhn_tan@263.net