基于曲面地表的弹箭射程计算方法

钟扬威,王良明

(南京理工大学能源与动力工程学院,江苏南京 210094)

基于曲面地表的弹箭射程计算方法

钟扬威,王良明

(南京理工大学能源与动力工程学院,江苏南京 210094)

为了研究地表曲面对弹箭射程的影响,基于Kane方法建立计及地表曲面、重力加速度大小和方向变化的改进刚体弹道模型,将大地线的概念引入到弹箭射程计算中,讨论大地主题反解法、正球体两点距算法、椭球体两点距算法、高斯投影距算法4种在曲面地表情况下计算射程的方法,比较改进刚体弹道模型和普通刚体弹道模型计算射程的差异。计算结果表明,在300 km范围内,椭球体两点距算法计算射程具有较高的精度,可作为曲面地表上的射程计算方法;考虑地表曲面后,采用改进刚体弹道模型比普通刚体弹道模型精度更高。

兵器科学与技术;曲面地表;弹道模型;射程

0 引言

在弹箭的弹道计算过程中,通常假设地表为平面,即认为地表与地面坐标系y=0平面重合,重力加速度方向也始终竖直向下。实际上,地球表面是一个曲面。在考虑曲面地表后,弹道的落点并不是地面坐标系的y=0,并且重力加速度的大小和方向也是时刻变化的,因此,椭球地表会对弹箭的射程产生影响。目前,在外弹道计算和射表编制中,多采用修正理论对此偏差进行处理。许多学者为解决这一问题做了研究,文献[1]给出了考虑正常重力和椭球地表的弹道模型,虽然很精确,但其模型复杂,计算量大,使用起来不是很方便。文献[2]中提出了使用射向内切圆逼近椭球地表的圆球地表模型,这种方法简单,具有一定的精度,但其只适用于射程在100 km以内的弹道。文献[3]设计了一种落点坐标系弹道模型,计算表明对质点弹道精度很高,但对6自由度弹道的精度没有考虑。本文给出了一个计及曲面地表和重力加速度大小、方向变化的改进刚体弹道模型,分析了射程计算方法,比较了两种弹道模型的计算差异。计算结果表明,在300 km范围内,椭球体两点距算法精度较高且公式简便,可作为曲面地表上的射程计算方法。曲面地表对弹箭的射程影响较大,在100 km范围内最大差异可达1 km,且其影响随射程、纬度和射向的变化而不同。为了减小射程计算差异,可采用本文建立的改进刚体弹道模型及射程计算方法。

1 坐标系及其转换关系

1.1 坐标系的定义

1)惯性坐标系Oexiyizi:不随地球自转,Oe为地心,Oezi轴沿地球自转轴,Oexi和Oeyi轴在赤道平面内,指向太阳系外的任意恒星,构成右手正交系。忽略地球公转。

2)地心坐标系Oexeyeze:Oe为地心,Oeze轴沿地球自转轴,Oexe轴在赤道平面内,与零度子午线相交,Oeye轴与Oeze轴和Oexe轴构成右手正交系。

3)地理坐标系Cxgygzg:C为弹箭质心,Cyg轴垂直当地水平面,沿当地垂线向上为正,Cxg轴和Czg轴在当地水平面内,分别沿当地经线和纬线的切线方向,Cxg轴指向北,Czg轴指向东。

4)发射坐标系Cxfyfzf:C为弹箭质心,发射坐标系由地理坐标系绕Cyg轴转动-ψ0角得到。Cxfyf称为射击面,ψ0角称为射击方位角。

5)弹轴坐标系Cξηζ:C为弹箭质心,Cξ轴沿弹轴方向,Cη轴和Cζ轴在垂直弹轴的平面内,与Cξ轴构成右手正交系。弹轴坐标系可视为由发射坐标系按3-2次序转动φ1和-φ2角得到。

1.2 坐标系转换关系

根据以上坐标系的定义,坐标系的转换可用四元数来表示。

从地理坐标系到发射坐标系的四元数qψ为

2 改进刚体弹道模型

2.1 弹箭运动方程组

利用弹箭Kane动力学原理,考虑地表为椭球面,经过推导,得到弹箭的一般运动方程组,可表示为

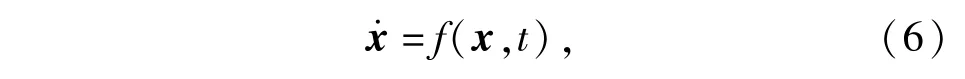
式中:x=[u1u2u3u4u5u6φ1φ2γ B L H]T,其中u1、u2、u3表示弹丸在地理坐标系3个方向上的速度,u4、u5、u6表示弹丸在弹轴坐标系3个方向上的转动角速度,φ1、φ2和γ分别为弹轴高低角、弹轴方位角和滚转角,B、L和H分别为地理纬度、地理经度及高度。

2.2 惯性矩阵、广义力矩阵和广义惯性力矩阵

矩阵mpq、fp和Δf*

p中元素的求法如下:

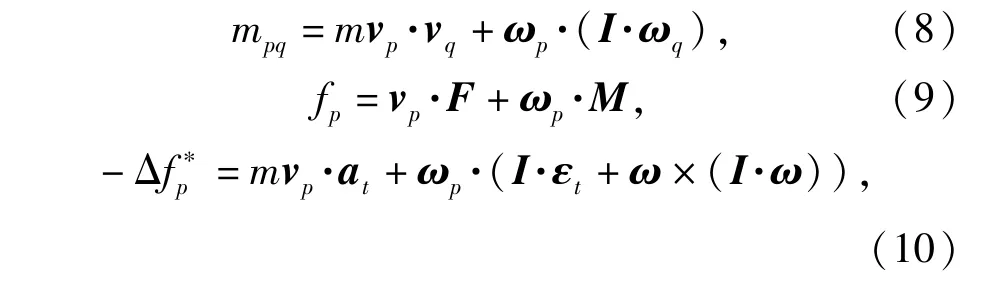
式中:I、vp、ωp、at、εt分别为弹箭的转动惯量矩阵、偏速度向量、偏角速度向量、加速度向量和角加速度向量;F和M分别为弹箭所受合力和合力矩向量;m为弹箭质量。

2.3 偏速度、偏角速度和加速度及角加速度

弹箭的偏速度vp和偏角速度ωp按表1计算,表中:iE、iN、iU分别表示地理坐标系三轴的单位向量;iξ、iη、iζ分别表示弹轴坐标系三轴的单位向量。

表1 偏速度和偏角速度Tab.1 Partial velocity and partial angular velocity

式中:R0为某纬度上考虑了该纬度的离心加速度影响所选取的有效地球半径[4],通常可取为地球的平均半径;g0为海平面处的重力加速度,根据1979年国际地球物理及大地测量联合会推荐的正常重力公式为

3 曲面地表时的弹箭射程及计算方法

大地线是连接椭球面上两点的最短线,它具有平面上的直线和球面上的大圆弧类似的特性。因此,考虑地表为椭球面时,弹箭的射程应当是椭球地表上,介于弹道起点和落点之间的大地线长度。

3.1 大地主题反解法

椭球面上点的大地经度L、大地纬度B和两点间的大地线长S叫做大地元素。已知两点的经纬度,计算它们之间的大地线长,叫做大地主题反解。

椭球面上的大地主题解算比平面和球面上的相应计算复杂,这是因为椭球面上的数学性质比平面和球面复杂。由于对计算精度的要求不同及计算工具和技术的发展,许多测量学者提出了种类繁多的解算公式和方法。文献[5]中介绍了几种典型的计算公式和方法。本文在下面的计算中采用的是高斯平均引数大地主题反解公式和贝塞尔大地主题反解公式计算两点间的大地线长。

3.2 近似计算

由于大地主题解算公式复杂,且常需要进行迭代,计算不是很方便,目前发展了多种计算椭球面上两点间距离的近似算法。

3.2.1 正球体两点距算法

设地球上弹道起点O的经纬度坐标为(LO, BO)、弹道落点C的经纬度坐标为(LC,BC),当将地球视为正球体时,则两点的距离D的计算公式为

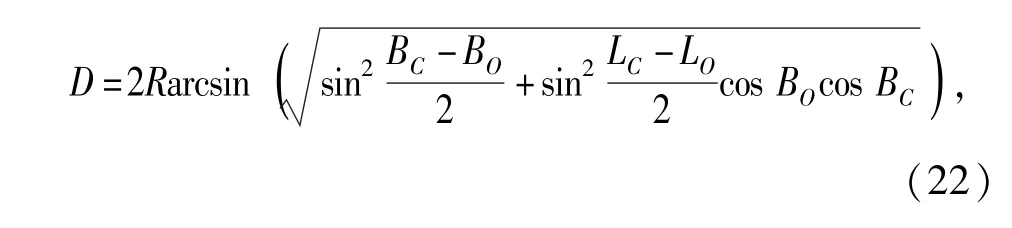
式中:R取地球平均半径。

3.2.2 椭球体两点距算法

地球参考椭球上的任意一点的大地经纬度和高度坐标(L,B,H)与地心直角坐标(x,y,z)的变换关系式为[6]

考虑地表为曲面,则使用两点间的贴地面弧长D作为两点间的距离更接近实际情况,修正弧长

3.2.3 高斯-克吕格投影距算法

高斯-克吕格投影属于地图投影的一种,地图投影是建立椭球面与平面上点与点的一一对应关系,其按投影面、投影变形性质的分类方法很多,文献[5]中介绍了几种常用的投影计算公式。

本文计算采用高斯六度带投影法,空间大地坐标系转换成平面直角坐标系的计算公式为

4 计算结果与比较

4.1 不同射程计算模型计算比较

为比较几种不同的射程计算方法计算射程的差异,在不同纬度上选取起点,在不同距离上选取落点,起点经度都选取为东经115°,用上文4种方法计算两点间距离,其中椭球体取1975年国际地球物理及大地测量联合会推荐的椭球参数,正球体半径取地球平均半径,结果如表2所示。

由大地主题反解法算出的距离精度最高,可作为标准值。由表2可以看出,在不同纬度和不同距离上,由椭球体两点距算法算出的距离和标准值基本相同。正球体两点距算法有明显的偏差,最大相对偏差为0.24%,中纬度上偏差小于低纬度和高纬度。高斯投影距算法在不同纬度和距离上与大地主题反算法计算出的结果基本吻合,最大相对偏差为0.02%,可以看出高斯投影距算法计算精度较高。在精度允许的范围内,椭球体两点距算法公式简便,可作为弹箭射程的计算方法。

表2 不同计算方法射程计算差异Tab.2 The ranges calculated by different calculation methods

4.2 不同弹道模型计算比较

为了考察改进刚体弹道模型与文献[4]中6自由度刚体弹道模型计算射程的差异,以某型火箭弹为研究对象进行对比计算(通过改变火箭的装药质量来改变其射程),计算结果如表3所示。表中Xc、Xi分别为6自由度刚体弹道模型和本文的改进刚体弹道模型计算得到的射程,ΔX=Xc-Xi为两种模型计算的射程差。改进刚体弹道模型中,弹道起点经度为东经115°.

由表3可以看出,在相同的初始条件下,改进刚体弹道模型计算的射程随着纬度的升高而减小。在不同射程和纬度上,普通6自由度刚体弹道模型计算射程比改进刚体弹道模型计算的射程大,其差异随着射程的增大而增大,在100 km时最大射程差可达到1 000 m.射程越远,地表曲面对射程的影响越大。正北和正西射向时的射程差异大于正东和正南射向。正北和正西射向时的射程差异随纬度的升高而增大,而正东和正南射向时的射程差异随纬度的升高而减小。

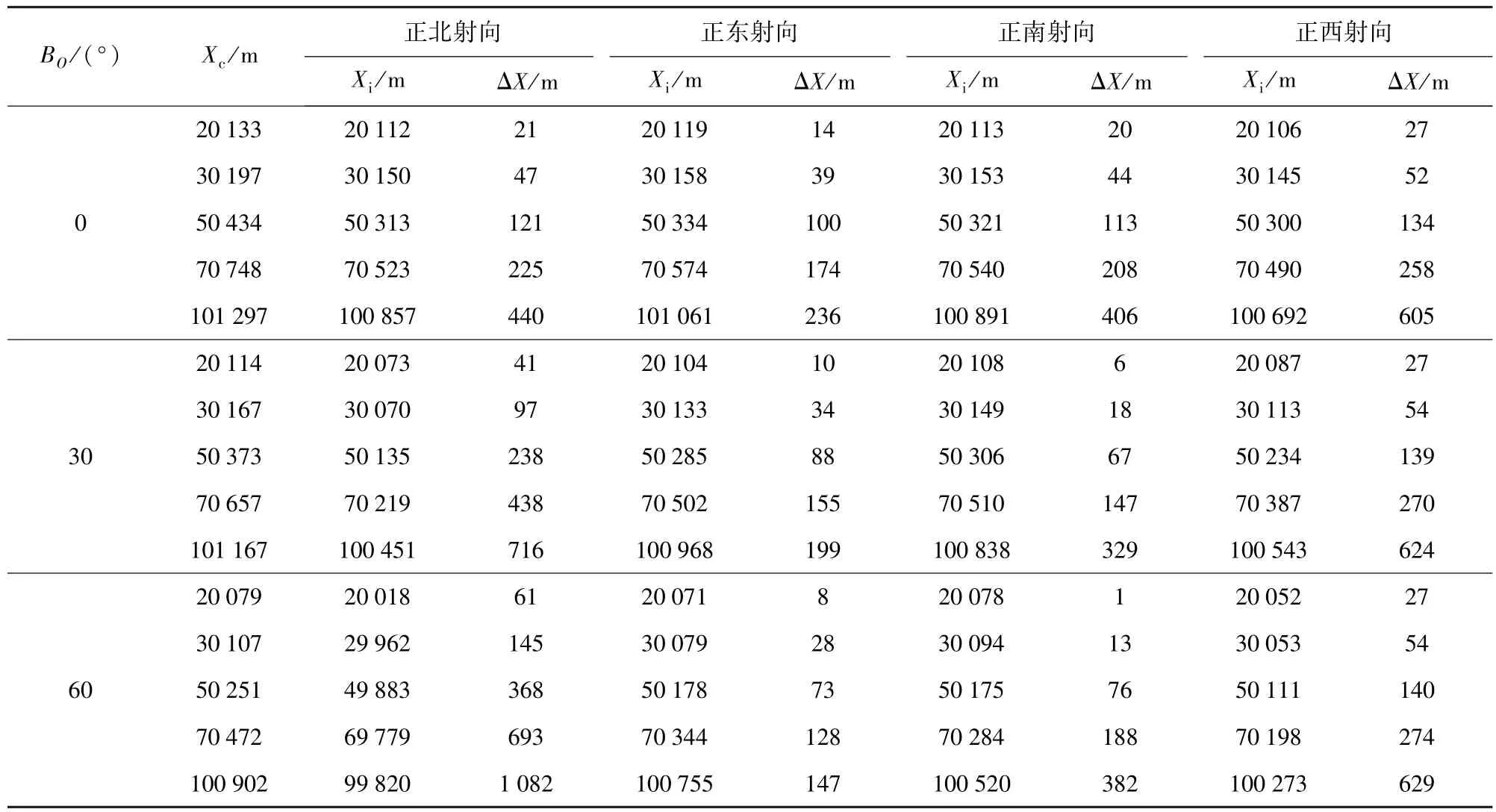
表3 不同弹道模型射程计算差异Tab.3 The ranges calculated by different ballistic models

5 结论

本文建立了基于地表曲面的改进刚体弹道模型,定义了地表曲面上的射程。讨论了射程计算方法,比较了两种弹道模型计算射程的差异。不同射程计算方法计算结果表明,在300 km范围内,大地主题反解法和椭球体两点距算法精度最高,高斯投影距算法精度也较高,最大偏差为0.02%,正球体两点距算法偏差较大,最大偏差可达0.24%.在精度允许的范围内,椭球体两点距算法计算公式简单,因此在射程计算时可采用该方法。两种弹道模型计算结果显示,曲面地表对弹箭的射程影响随射程、纬度和射向的变化而不同。射程越远,影响越大。正北和正西射向时的影响大于正东和正南射向。正北和正西射向时的影响随纬度的升高而增大,而正东和正南射向时影响相反。本文建立的改进刚体弹道模型及射程计算方法对于射表编制、试验射程标准化及弹箭设计有一定的参考价值。

References)

[1] 林献武,王中原,王天明,等.正常重力和椭球地表对弹道计算的影响[J].南京理工大学学报,2009,33(5):607-611.

LIN Xian-wu,WANG Zhong-yuan,WANG Tian-ming,et al. Effect of normal gravity and ellipsoid earth surface on trajectory calculation[J].Journal of Nanjing University of Science and Technology,2009,33(5):607-611.(in Chinese)

[2] 林献武,王中原,常思江.曲面地表对弹道影响的一种计算方法[J].弹道学报,2008,20(4):12-15.

LIN Xian-wu,WANG Zhong-yuan,CHANG Si-jiang,et al.A calculation method for influence of curved earth surface on calculating trajectory[J].Journal of Ballistics,2008,20(4):12-15.(in Chinese)

[3] 刘鹏云,薛晓中,孙瑞胜,等.曲面地表对远程火箭弹弹道影响的计算方法[J].火力与指挥控制,2012,37(8):44-46.

LIU Peng-yun,XUE Xiao-zhong,SUN Rui-sheng,et al.A calculation method for influence of curved earth surface on far range rocket projectile calculating trajectory[J].Fire Control and Command Control,2012,37(8):44-46.(in Chinese)

[4] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社, 2008:127-143.

HAN Zi-Peng.Exterior ballistics of projectiles and rockets[M]. Beijing:Beijing Institute of Technology Press,2008:127-143. (in Chinese)

[5] 熊介.椭球大地测量学[M].北京:解放军出版社,1988:109 -165.

XIONG Jie.Ellipsoidal geodesy[M].Beijing:Chinese People's Liberation Publishing House,1988:109-165.(in Chinese)

[6] 卫宇.考虑地球曲率情况下两点距离问题的求解[J].航空兵器,2008,6(3):7-12.

WEI Yu.Solution of distance between two points considering curvature of the earth[J].Aero Weaponry,2008,6(3):7-12.(in Chinese)

Method of Calculation on the Range of Projectiles and Rockets Based on Curved Earth's Surface

ZHONG Yang-wei,WANG Liang-ming
(School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

To study the effects of curved earth's surface on the ranges of projectiles and rockets,a modified rigid body trajectory model is built based on Kane method in which the curved earth's surface and the changes in both the size and direction of the gravity acceleration are considered.The concept of geodesic line is introduced to the range calculation of projectiles or rockets.Four calculation methods for the range under the condition of curved earth's surface are discussed,such as inverse solution of geodetic problem and so on.The range errors calculated with the modified rigid body trajectory model and the ordinary rigid body trajectory model are compared.The result shows that the spheroidal distance algorithm has a high calculation precision in the range of 300 km,and can be used to calculate the range on the curves earth's surface.The modified rigid body trajectory model is more accurate than the ordinary rigid body trajectory model in the consideration of the curved earth's surface.

ordnance science and technology;curved earth's surface;trajectory model;range

TJ012.2

:A

:1000-1093(2014)08-1187-06

10.3969/j.issn.1000-1093.2014.08.008

2013-07-22

钟扬威(1989—),男,博士研究生。E-mail:zyw_601@163.com;王良明(1963—),男,教授,博士生导师。E-mail:lmwang802@163.com