引信用磁耦合谐振系统复杂环境能量损耗分析

李长生,李炜昕,2,张合,丁立波

(1.南京理工大学智能弹药技术国防重点学科实验室,江苏南京 210094;2.上海无线电设备研究所,上海 200090)

引信用磁耦合谐振系统复杂环境能量损耗分析

李长生1,李炜昕1,2,张合1,丁立波1

(1.南京理工大学智能弹药技术国防重点学科实验室,江苏南京 210094;2.上海无线电设备研究所,上海 200090)

针对复杂铁磁环境中磁耦合谐振装定系统无法有效工作的问题,基于电磁准静态场基本理论,推导磁耦合谐振装定系统涡流损耗解析表达式,分析该系统能量传输的影响因素。对不同介质环境中的装定系统进行数值模拟和实验研究,研究结果表明:理论分析与数值计算、实验结果趋于一致;涡流损耗为该系统不能正常工作的主要原因,且与系统的谐振频率、介质材料的磁导率和电导率相关;若在钢介质的开槽间隙中加入铁氧体磁环,装定系统20 ms后可以正常工作,能满足引信的装定要求;该结论对磁耦合谐振装定系统在复杂环境下的工程化设计提供参考。

兵器科学与技术;磁耦合谐振;引信;装定系统;复杂铁磁环境;能量传输;涡流损耗

0 引言

随着武器系统信息化的发展,小口径弹药电子引信得到了广泛的应用,如美国的理想单兵作战武器、瑞士的“空中卫士”AHEAD弹、单兵空炸火箭弹等。为了提高武器系统的毁伤性能,引信的无线装定技术成为能量和信息同步传输的关键技术,现阶段各国普遍采用并得到广泛应用的是电磁感应装定技术。但是,由于电磁感应基于变压器松耦合作用机理,装定系统存在初次级耦合线圈的有效工作距离较近、线圈匝数多、传输功率小及传输效率低等缺点,在一些特殊场合无法满足引信与火控系统之间的动态、快速信息交联。

磁谐振式无线能量传输技术因其具有近场传输非辐射性、高效性,能够进行较远距离能量传输等优点,在植入式医疗器件、电动汽车充电及武器系统等领域进行了相关研究[1]。对于武器系统平台,装定系统周围存在复杂的铁磁环境,金属介质在发送和接收模块形成的交变磁场中会改变谐振线圈的电路参数及产生功率损耗[2-3]。磁耦合谐振能量传输的特点决定了其损耗具有一定的特殊性,因受到松耦合、谐振作用等因素的影响[4],具有谐振线圈中谐振电压高、谐振电流大、谐振频率高等特点。因此,分析其损耗原因和研究其损耗特性,对优化设计磁耦合谐振装定系统,提高抗干扰性具有一定的研究意义。

目前,国内外大量文献[5-7]对磁耦合谐振无线能量传输的传输效率和传输功率等传输特性进行了深入的分析,提出了提高传输质量的优化方法。但是,对于复杂环境中磁耦合谐振系统的功率损耗和传输规律的研究还未深入开展,针对此部分的研究还较少,未检索到相关文献。本文针对小口径引信,基于电磁准静态场等理论,建立了磁耦合谐振装定系统功率损耗数学模型,分析了磁耦合谐振能量传输的影响因素,并提出了优化设计方法。

1 磁耦合谐振系统结构特点

根据电磁谐振耦合式能量传输原理[1,4],建立如图1的磁耦合谐振装定系统电路拓扑模型,包括初级发射模块(由驱动线圈A和谐振电路S组成)和次级接收模块(由谐振耦合电路D和接收线圈B组成)。初级发射模块通过高频信号发生电路、功率放大电路在驱动线圈A周围产生具有一定频率f0的磁场;谐振电路S通过电磁感应接收驱动电路的能量信号,引信体上的谐振电路D与谐振电路S具有相同的谐振频率而发生谐振从而实现能量传输,拾取线圈B通过感应从D中获取能量。该能量一方面经过信息解调电路将装定信息记录在微处理器中,一方面经过后续整流电路将能量储存在电容C中。对于谐振电路S和D的工作频率可以通过接入外部电容(CS、CD)调节到相同的频率f0.

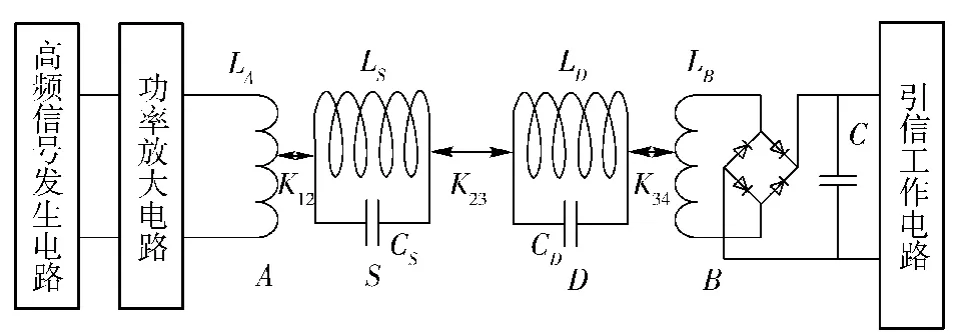
图1 磁耦合谐振电路拓扑模型Fig.1 Model of resonant coupling circuits based on magnetic resonant coupling

磁耦合谐振装定系统耦合结构即传输通道如图2所示,主要分为初级骨架、次级磁芯、初级发射模块、次级接收模块和引信电路,图中金属介质为武器平台供弹通道校正体的材料。磁耦合谐振装定系统由信号发生电路、功率放大电路在初级发射模块周围产生周期变化的电磁场,向周围金属介质和次级接收模块进行电磁扩散;同时次级接收模块通过电磁谐振产生谐振电压,在次级磁芯中也会感应涡流。

图2 磁耦合谐振系统耦合结构剖面图Fig.2 The cutaway view of magnetic resonant coupling system

上述电磁谐振耦合式装定方式具有以下优越性:传输效率高,可在较远距离进行能量和信息的传输;与电磁感应装定方式相比,能量激活速度快、线圈匝数少;与炮口感应装定相比,装定时间窗口长,初级发射模块使用寿命长,提高了引信装定信息的可靠性和装定系统的使用寿命。

2 数学模型

2.1 涡流场计算模型

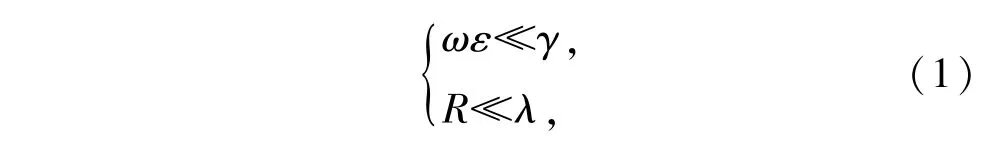
式中:ω为电磁场角频率;γ为电导率;λ为电磁场波长;ε为身管的介电常数。(1)式可看作导体内磁准静态场近似成立的条件。

对准静态场,可忽略位移电流∂D/∂t,得

根据相应的边界条件和(4)式的二阶微分方程,可计算其涡流场[8-10]的分布。

2.2 磁芯分析

对于磁芯,如图3所示,假设电磁谐振系统次级接收模块的磁芯介质磁导率为μ,电导率为γ,为简化分析磁芯可看作为圆柱形,长度可看作为无限长;设细长磁芯的半径为R,接收模块中交变电流的角频率为ω.采用圆柱坐标,按轴对称场进行计算[10],假设磁芯无限长,磁场只有轴向方向z分量,且只与半径有关,感应涡流仅有周向分量Jθ.

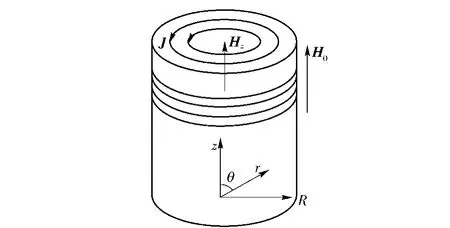
图3 磁芯的模型Fig.3 Model of core

由贝塞尔函数的递推公式,可得

2.3 铁磁环境分析

对于初级耦合结构,如图4所示,假设发射模块中交变电流的角频率为ω,初级骨架为非金属材料,外围校正体为金属介质,金属介质的内径为Ri,外径为Ro.仍为解电磁扩散方程(4)式的问题,同样采用圆柱坐标,按轴对称场进行计算。该问题的边界条件为

图4 初级耦合结构的模型Fig.4 Model of primary coupling structure

金属介质在无限远处的磁场强度H应为0,即当kr→∞时,H(r)→0,根据贝塞尔函数的性质,可得

由此,可计算单位长度内金属介质的涡流损耗为

2.4 损耗的优化措施

由磁耦合谐振系统涡流损耗(13)式、(17)式可知,功率损耗的大小与磁耦合谐振系统的谐振频率、介质材料的磁导率和电导率相关。引信信息交联系统的工作频率主要由装定数据传输速率和初次级模块耦合时间窗口决定,这里假设系统谐振频率1 MHz.初级耦合结构校正体需要承受弹丸和自动机后坐力等强大的冲击,一般采用高强度钢材料或者钛合金材料。因此,只能通过改变磁路和介质材料来减少装定系统的功率损耗。

磁耦合谐振能量耦合属于近场耦合,是电磁耦合的一种特殊形式。因此,依据磁屏蔽基本原理,可选用高磁导率材料作为次级接收模块的磁芯,使次级接收模块可以更多地得到初级发射模块产生的磁场。由于磁耦合谐振系统的特殊性及涡流损耗的存在,磁芯介质应选用低电导率材料。同理,初级发射模块应该尽量远离金属介质(涡流损耗)和高磁导率介质(磁路)。该系统可对校正体结构进行适当的开槽处理,增大初级发射模块与金属介质的距离,为了简化计算这里仅对耦合窗口进行圆形方式开槽;考虑到涡流损耗的影响远大于磁路对能量传输损耗的影响,可在发射模块与金属介质的间隙间加入高磁导率、低电导率材料介质。

由安培环路定律和电感定义,可得到有介质存在的电感值

式中:μ0为真空中的磁导率;la为气隙长度;μr为相对磁导率;lm为介质磁路长度;S为磁路平均截面积。

谐振线圈在介质环境的影响下,将改变固有的电路谐振参数,根据磁耦合谐振能量传输的特征,非辐射谐振通道参数的改变将会影响整个系统的正常工作。因此,谐振系统在加入优化措施后,谐振线圈的谐振频率仍需匹配至系统谐振频率。

3 仿真分析

为简化仿真模型,减少计算时间,将驱动线圈A和接收线圈B的电参数分别映射至谐振电路S和谐振电路D中,利用二端口网络原理及磁谐振原理,基于HFSS软件建立两谐振电路仿真模型,根据上述分析的优化措施分别进行数值计算,初次级模块的磁场强度散布如图5所示。仿真参数:发射功率2 W,初次级谐振线圈半径15 mm,谐振电感24.7 μH,谐振电容1 nF,耦合距离15 mm.

图5 磁场强度散布图Fig.5 Scatter plot of magnetic field strength

由图5可以看出:磁耦合谐振装定系统在周围没有介质影响的空气条件下,次级谐振电路可以正常获得初级电路发送的磁场能量;接收模块加入铝介质磁芯,由于介质的涡流损耗,接收模块仅能接收到较少的磁场能量;接收模块加入铁氧体磁芯,介质的高磁导率使次级获得到更多的磁通量,介质的低电导率降低了涡流损耗,接收模块获得比正常情况下更多的磁场能量;初级发射模块周围加入钢介质,由于钢的涡流损耗及对磁路的影响(磁屏蔽)使得接收模块几乎接收不到磁场能量;初级介质做开槽处理,虽然较多的磁场被介质束缚,但仍有较少磁场能量被接收模块获得;初级发射模块与钢介质的间隙加入铁氧体,虽然减少了大量的涡流损耗,但是高磁导率的铁氧体束缚了磁场,接收模块只可以获得发射模块的部分能量。

图6为初次级模块距离30 mm,不同介质环境下的负载功率随工作频率变化的仿真与实验曲线。从图6可以看出:收发端均在空气中时传输效率最高;在发射模块被钢介质包裹和接收模块磁芯为铝介质情况下,接收模块仅能接收到微弱的能量;发射模块加入铁氧体磁环后,传输效率较开槽方案传输功率高;仿真结果与实验结果较一致,存在的误差与线圈损耗、谐振频率的偏移等相关。

图6 负载功率随工作频率的变化曲线Fig.6 Variation curves of load power with frequency

4 实验验证

为验证理论分析与仿真计算的正确性,设计了不同介质环境条件下装定系统的能量传输实验,实验装置如图7所示。实验优化参数:发射功率2 W,驱动线圈和接收线圈5 μH,两谐振线圈26 μH,谐振电容1 nF,负载无感电阻50 Ω,发射模块和接收模块线圈半径为15 mm.

由于理论计算仅考虑系统工作在谐振状态的能量损耗,因此无法计算非谐振状态下的能量损耗,这里给出了谐振状态下负载功率随耦合系数的变化曲线,如图8所示。不同耦合结构的负载功率变化规律不一致,最优负载接收功率分别在不同的耦合系数处获得;铁磁材料会影响传输通道电路工作状态,改变谐振电路能量传输特性;理论计算和实验结果有较好的一致性,开槽和铁氧体优化措施可以较好地提高系统传输功率。

图7 实验装置Fig.7 Experimental equipment

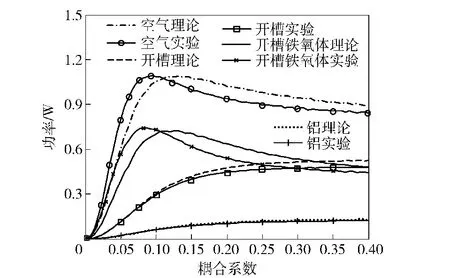
图8 负载功率随耦合系数的变化曲线Fig.8 Variation curves of load power with coupling coefficient

表1为不同磁芯材料、空气环境、无感电阻条件下,接收线圈的输出电压值和传输通道的传输效率。从表1可以看出,由于铝磁芯涡流损耗的存在,接收线圈只能获得很低的电压,而经过处理后的薄片铝磁芯阻断了涡电流的形成,但是仍有较大的功率损耗;铁氧体磁芯较空气环境有较明显的优势。

采用不同优化措施对装定系统进行静态实验,引信储能电容47 μF的充电曲线如图9所示。在发射模块周围包裹钢介质,磁芯介质为铝等金属介质情况下,接收线圈接收到较少的能量,且充电速度较慢,不能满足引信装定的要求。对初级钢介质校正体进行开槽处理,储能电容充电电压可以有效提高,但是充电速度依然较慢。若在钢介质的开槽间隙中加入铁氧体磁环,装定系统20 ms后即能正常工作,满足该引信的装定要求。

表1 不同磁芯材料下接收线圈的输出电压Table 1 Output voltages of receiving coils with different material cores

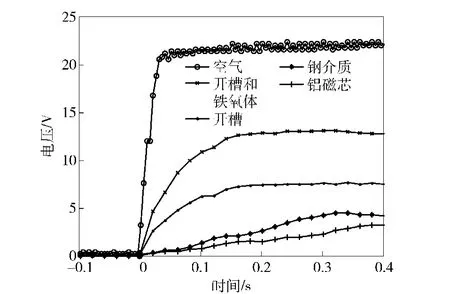
图9 储能电容充电曲线Fig.9 The charging curves of energy storage capacitor

5 结论

本文基于电磁准静态场理论,建立了磁耦合谐振装定系统涡流损耗数学模型,分析了磁耦合谐振能量传输影响因素,并通过仿真计算和实验验证得出以下结论:

1)影响磁耦合谐振系统正常工作的原因是涡流损耗和磁路,其中涡流损耗起着主要作用。

2)涡流损耗的大小与磁耦合谐振系统的谐振频率、介质材料的磁导率和电导率相关。

3)由于磁耦合谐振原理的特殊性,谐振系统在加入介质或优化措施后,谐振线圈的谐振频率仍需匹配至系统谐振频率。

4)若在铝介质的开槽间隙中加入铁氧体磁环,装定系统可以正常工作,可以满足引信的装定要求。

5)理论分析与数值计算、实验结果有较好的一致性,这对磁耦合谐振装定系统在复杂环境下的工程化设计提供参考。

References)

[1] Kurs A,Karalis A,Moffatt R,et al.Wireless power transfer via strongly coupled magnetic resonances[J].Science,2007,317: 83-86.

[2] 周晓东,张河.用于引信的能量和信息非接触同步传输技术[J].兵工学报,2003,24(3):424-426.

ZHOU Xiao-dong,ZHANG He.Contactless synchronous transmission of power and information for fuze[J].Acta Armamentarii, 2003,24(3):424-426.(in Chinese)

[3] 吴志亮,张合.小口径引信膛内感应储能磁场穿透特性[J].兵工学报,2010,31(10):1310-1315.

WU ZHi-liang,ZHANG He.The magnetic field penetration characteristics in bore of small caliber fuze using inductive energy[J]. Acta Armamentarii,2010,31(10):1310-1315.(in Chinese)

[4] 李长生,张合.基于磁共振的引信用能量和信息无线同步传输方法研究[J].兵工学报,2011,32(5):537-542.

LI Chang-sheng,ZHANG He.Research on wireless power and information synchronous transmission method based on magnetic resonance for fuzes[J].Acta Armamentarii,2011,32(5):537-542.(in Chinese)

[5] Karalis A,Joannopoulos J D,Soljacic M.Efficient wireless nonradiative mid-range energy transfer[J].Annals of Physics,2008, 323:34-48.

[6] Sample A P,Meyer D A,Smith J R.Analysis.Experimental results,and range adaptation of magnetically coupled resonators for wireless power transfer[J].IEEE Transactions on Industrial Electronics,2011,58(2):544-554.

[7] Imura T,Okabe H,Hori Y.Basic experimental study on helical antennas of wireless power transfer for electric vehicles by using magnetic resonant couplings[C]∥Vehicle Power and Propulsion Conference.Dearborn,MI:IEEE,2009:936-940.

[8] 胡文江,胡先权.似稳条件下导体圆柱面内电流分布的求解[J].重庆大学学报:自然科学版,2001,24(4):55-57.

HU Wen-jiang,HU Xian-quan.Solution of the eddy current distribution inside a condutor cylindrical boundary surface for quasisteady-state[J].Journal of Chongqing University:Natural Science Edition,2001,24(4):55-57.(in Chinese)

[9] 冯慈璋,马西奎.工程电磁场导论[M].北京:高等教育出版社,2000.

FENG Ci-zhang,MA Xi-kui.An introduction to engineering electromagnetic fields[M].Beijing:Higher Education Press,2000. (in Chinese)

[10] Cardelli E,Torre E D,Pinzaglia E,et al.Analysis of magnetic losses of cylindrical cores in the frequency domain[J].IEEE Transactions on Magnetics,2003,39(3):1365-1368.

[11] 冉杨强.数学物理方法[M].重庆:西南师范大学出版社, 2008.

RAN Yang-qiang.Methods of mathematical physics[M]. Chongqing:Southwest China Normal University Press,2000.(in Chinese)

Research on Energy Loss of Fuze Setting System Based on Magnetic Resonant Coupling in Complex Environment

LI Chang-sheng1,LI Wei-xin1,2,ZHANG He1,DING Li-bo1
(1.ZNDY of Ministerial Key Laboratory,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China; 2.Shanghai Institute of Radio Equipment,Shanghai 200090,China)

In order to solve the problem of that magnetic resonant coupling setting system can not work effectively in complex ferromagnetic environment,an analytical expression of eddy current losses of magnetic resonant coupling setting system is derived based on the basic theory of the electromagnetic quasi-static field,and the influence factors of the energy transmission system are analyzed.Numerical simulation and experiment study are conducted on the fuze setting system in different environments.The results show that theoretical analysis results are consistent with the numerical calculation and experimental results.The system is not working properly mainly due to eddy current loss,which is related to the resonant frequency of the system,and the permeability and conductivity of dielectric material.When ferrite bead is added in slot gap of steel media,the fuze setting system can work effectively after 20 ms,and can meet the requirement.The conclusion on magnetic resonant coupling setting system is helpful to engineering design in complex environment.

ordnance science and technology;magnetic resonance coupling;fuze;setting system;complex ferromagnetic environment;wireless power transmission;eddy current loss

TJ43

:A

:1000-1093(2014)08-1137-07

10.3969/j.issn.1000-1093.2014.08.001

2013-04-28

国家自然科学基金项目(61104185、61403201)

李长生(1984—),男,讲师。E-mail:lichangsheng1984@163.com;李炜昕(1986—),男,博士研究生。E-mail:weixin_li@126.com;张合(1957—),男,教授,博士生导师。E-mail:hezhangz@mail.njust.edu.cn