瞬时测频系统的线性调频信号分析及改进

王洪迅,王士岩,王星,王红卫

(1.西北工业大学自动化学院,陕西西安 710072;2.空军工程大学航天航空工程学院,陕西西安 710038; 3.中国人民解放军93286部队32分队,辽宁沈阳 110141)

瞬时测频系统的线性调频信号分析及改进

王洪迅1,2,王士岩2,3,王星2,王红卫2

(1.西北工业大学自动化学院,陕西西安 710072;2.空军工程大学航天航空工程学院,陕西西安 710038; 3.中国人民解放军93286部队32分队,辽宁沈阳 110141)

频率是雷达信号的关键特征之一,雷达告警(RWR)/电子支援(ESM)等电子战接收机多采用瞬时测频(IFM)技术来实时提取;线性调频(LFM)信号是一种重要的、雷达广泛应用的信号类型,但传统IFM无法检测LFM信号频率特征。提出一种新的基于改进IFM系统的LFM信号特征检测方法,基于IFM系统工作原理建立了LFM信号经过IFM系统的数学模型,并探讨了IFM系统对LFM信号检测的频率分辨力和最小可检测调频斜率。改进IFM系统采用整形检波信号作为采样有效指示信号,以提取LFM信号的到达时间(TOA)和脉冲宽度(PW);采用模数转换器(ADC)代替传统IFM的极性量化器对其正交通道输出进行连续采样,再通过解模糊、线性回归算法平滑去噪,估计出LFM信号的载频和调频斜率。仿真实验结果表明,改进IFM系统可在一个LFM脉冲内以较高的精度提取LFM信号特征,并保留了传统IFM系统的原有优点。

雷达工程;瞬时测频;线性调频信号;解模糊;线性回归

0 引言

机载雷达、雷达告警(RWR)/电子支援(ESM)接收机是作战飞机两种重要装备[1]。一方面线性调频(LFM)[2]信号是机载雷达中常用信号之一,因其作用距离远,距离分辨力强;另一方面 RWR/ ESM接收机通过探测雷达信号来识别载机所面临的威胁并进行告警,其多采用瞬时测频(IFM)技术提取信号频率特征,但由于传统IFM工作机理的限制,使得RWR/ESM无法通过IFM对LFM信号的检测进行威胁告警。

LFM信号主要有4个特征,其中两个频率特征:载频、调频斜率,两个时间特征:到达时刻(TOA)、脉冲宽度(PW).对于机载雷达而言,其所检测的是合作信号,除了回波TOA未知外,其他3个信号特征都已知;机载雷达有很多工作模式, LFM信号通常只在其测距过程中出现,即使出现也并不像其他类型信号那样连续多个脉冲的参数完全一致。但对于RWR/ESM接收机而言,其所检测的是非合作信号,无法提前预知4个LFM信号特征。为此首先RWR/ESM要在频域上“宽开”,通常需数十吉赫超宽频段覆盖;其次通常采用频率折叠技术、宽带窄带接收机结合的方式测频[1],利用宽频段滤波器的频段信息引导IFM测频,再用IFM测频结果引导窄带接收机本振,以对准待测雷达信号。IFM是RWR/ESM接收机中一种常用宽带接收机[3-4],文献[3-5]分析了传统IFM工作原理以及典型结构, IFM频率覆盖范围宽,频率分辨力高,可在一个脉冲持续时间内给出测量结果,但不能获得LFM信号调频斜率。文献[6]描述了IFM的发展进程、设计与性能准则,提出多种IFM及其在现代电子战(EW)系统中的应用,文献[7]讨论了基于现场可编程逻辑门阵列(FPGA)的IFM架构,但均未提及其对LFM信号的检测性能。随着技术的发展,数字接收机成为RWR/ESM进行精确测频的一种接收机,尽管其模数转换器(ADC)采样率可达数吉赫,但它仍然是窄带的,需要下变频,对本振进行引导,需要反应时间。当前还有很多对LFM信号的检测算法,如文献[8]讨论了FPGA应用时频分析实现对雷达脉内调制特征的检测,其中包括LFM信号;文献[9]利用双正交傅里叶变换(FT)算法分析LFM信号斜率;文献[10]提及多种对于LFM信号的电子侦察算法,并提出一种新的算法;文献[11]利用周期分数阶傅里叶变换(FRFT)算法实现线性调频连续波(LFMCW)信号的最优渐进估计;文献[12]基于正交匹配追踪的欠采样LFM信号参数估计;此外还有很多其他算法[13-14],但是这些算法需要大量计算资源,耗费大量运算时间,并事先要求准确对准雷达频点。故此尽管这些算法很先进,但不适用于RWR/ ESM接收机。

综上所述,尽管LFM是一种非常典型的雷达信号,但在当前技术条件下多数采用IFM的RWR/ ESM接收机并不具备实时检测LFM信号的能力。那么很自然的一个问题是:IFM到底能否实时检测LFM信号呢?本文为此展开研究。

1 IFM处理LFM信号的数学模型

迄今为止未见有文献探讨IFM如何检测LFM信号,为此首先结合传统LFM系统结构分析其局限,然后研究IFM处理LFM信号的数学模型。

1.1 传统IFM系统及其局限

图1 传统IFM系统结构Fig.1 Traditional IFM system structure

图1所示为传统IFM系统的典型结构[3-5],其主要有两种典型特征:

1)视频检波信号经整形,再经一定时间的延迟,形成锁存脉冲,从而获得信号测量结果。需要说明的是,因该部分电路及功能过于简单,传统IFM结构中通常不予说明。

2)极性量化器+编码矫正结构。为了快速获取测量结果,通常采用极性量化器;由于各个支路测量结果有模糊,通过编码矫正逻辑以获取正确的测量结果。

由于以上两个原因,导致传统IFM系统对某一雷达信号脉冲,只进行一次量化采样,输出为采样时刻的频率二进制码[1],仅能输出一个结果。

1.2 传统IFM信号处理模型

在对传统IFM信号处理模型的分析中[1]其核心为图1的微波鉴相器(MPD)[1-5](其典型结构如图2所示),且均假设MPD端口1馈入一个固定载频脉冲信号u(t)=2Acos ωt.则其输出UI、UQ为

图2 实用微波鉴相器结构Fig.2 Schematic diagram of practical microwave phase discriminator

(1)式中k为检波器的检波系数,A为信号幅度。其延迟线引入的相角φ可表示为

(3)式即为文献[3-7]的分析结果,传统上即依据该式获取信号载频。而且(3)式还表明,MPD中延迟线的延迟时间t0是一个很重要的参数。

1.2 MPD对LFM信号的处理模型

MPD是IFM的关键部件,延迟线则是MPD的核心器件。它对固定载频雷达脉冲可给出(3)式的结果,但对LFM信号(3)式显然无法描述LFM完整特征。因此需要研究该MPD对LFM信号的处理模型。若设图2的MPD端口1馈入一个LFM信号脉冲[2]为

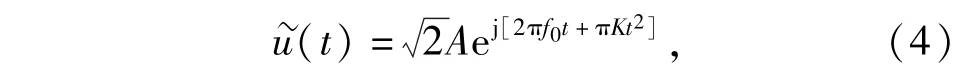
式中:f0为LFM信号载频;K为其调频斜率。则经过图2中后续功分器后上支路端口2信号为

(11)式为LFM信号经过MPD的I、Q两个正交通道输出的理论值,(13)式为相角与LFM信号的对应关系。实际IFM系统中延迟时间t0一般为纳秒量级,即使K为每微秒几十兆赫到几百兆赫,πKt20相对于2πf0t0很小,可忽略不计。为分析方便通常将(11)式和(12)式联立,修正为

典型IFM系统多采用图1所示的4路MPD并列构成,只是这些MPD延迟线长短不同(但这些延迟线长度存在一定关系),在覆盖较宽的频率范围的同时,并获得一定的测频精度。若设其中最短延迟线的延迟时间为t0,一般其他3路延迟线的长度分别依次为4t0、16t0、64t0.若有一个(4)式所示的LFM信号输入该IFM系统,则其4路MPD输出的UI、UQ电压值及相位φ可分别表示为

注意(4)式LFM信号频率表示为f=f0+Kt/2, (19)式与之是有区别的。再者(14)式～(18)式中隐含关系φi=arctan(UI-i/UQ-i),其中i表示各支路标号。

2 IFM系统改进

由(14)式～(19)式可知IFM系统具备实时检测LFM信号频率特征的潜力,但由于图1所示传统IFM结构的限制,使得其不具备检测LFM的能力,须对其加以改进。

2.1 改进的IFM系统

综上所述,对于一个雷达脉冲传统IFM只能得到一个频率采样值,其对LFM信号也是如此。因此需要对现有IFM系统进行改进。一种改进IFM如图3所示,具有如下两个典型特征:

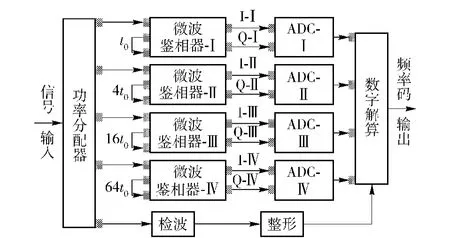
图3 改进后的IFM系统Fig.3 Improved IFM System

1)信号检波包络经过整形后,不再作为锁存信号,而是一方面作为采样有效信号,另一方面用于提取对应LFM信号的TOA和PW特征。

2)采用高精度ADC代替量化器,在采样有效信号的指示下,分别用ADC对各MPD输出的UI、UQ通道进行连续采样。

3)通过数字解算获得信号频率特征。图3中根据(3)式或(13)式可得各采样点的离散频率值;再对4路MPD输出的离散频率值做解模糊处理;最后应用一元线性回归算法[3]对Ⅳ支路输出精度较高的离散频率值进行平滑去噪,从而估计出LFM信号的载频、调频斜率。

2.2 频率模糊修正方法

其次是频率模糊修正。经过对反正切模糊修正后,短延迟线Ⅰ支路可输出正确频率值,但精度不高;但因Ⅱ、Ⅲ、Ⅳ支路的延迟时间过长,相位φ大于2π,故存在频率模糊。需根据4个支路之间4倍相位关系修正模糊。图3中应使用前一支路的计算频率值修正后一支路的模糊频率值,如用Ⅰ支路的频率值修正Ⅱ支路的模糊频率值,再用修正的Ⅱ支路频率值修正Ⅲ支路的模糊频率值;依此类推,最后对Ⅳ支路输出修正,得到精度较高的频率值。

2.3 LFM信号测频精度分析

改进IFM系统对UI、UQ连续采样量化,而不是传统IFM中的极性量化,对(3)式求全微分,得这种IFM系统的频率分辨力表达式为

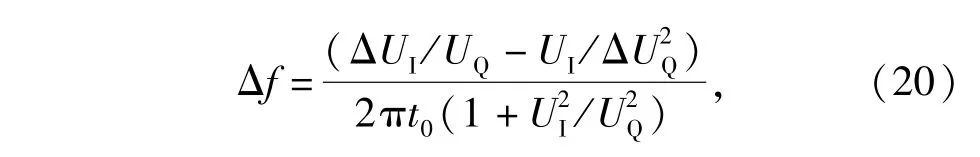
式中:ΔUI、ΔUQ分别是ADC对UI、UQ的量化间隔。该式还表明,图3所示的IFM系统频率分辨力与传统IFM系统相同,同样取决于最后一个支路,需依据最长延迟时间进行修正。此外由于改进IFM对LFM信号进行连续多次采样,每次采样均可对应一个测频精度,其可以表示为

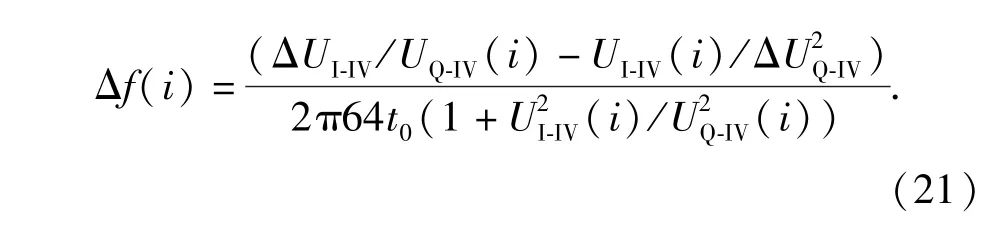
由(21)式可知,若输入为LFM信号,则IFM输出的UI、UQ随时间变化,故Δf(i)也是变化的。为了评估改进IFM系统测频精度,本处定义其频率分辨力Δfmin=max[Δf(i)],即IFM对某次LFM信号连续测量的最劣精度(对应误差的最大情况),只有Δfmin满足精度要求,改进的IFM系统才可用于LFM信号的有效检测。

2.4 最小可检测调频斜率分析

改进IFM系统若可检测LFM信号,主要是检测信号的调频斜率K,但K很小时系统将无法检测LFM信号。对(19)式变形得

考虑到多次连续采样的影响,对K求f的导数,可得每次采样对应K分辨力ΔK(i)为

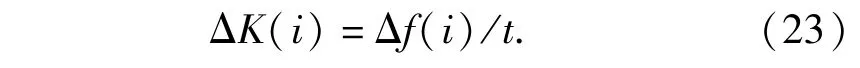
由(23)式可以看出ΔK(i)与Δf(i)的关系。由于该处欲求K的分辨力(设其表示为ΔKmin),因此该处应代入频率分辨力Δfmin;LFM信号持续时间即其脉宽PW=τ,由此改进IFM系统对LFM信号的最小可检测调频斜率ΔKmin,可表示为

3 仿真验证及分析

为验证上述LFM信号处理模型,通过仿真进行验证和分析;仿真验证分别从图3所示改进IFM系统的4个关键信号处理环节进行,最后分析信号噪声比SNR对参数误差的影响。首先规定验证条件,设其输入的LFM信号特征如下:载频f0为4 GHz,调制系数K为20 MHz/μs,信号幅度A为2 V,脉冲宽度τ为10 μs;为便于分析不考虑LFM信号脉冲的TOA.

3.1 MPD输出

受外部环境、各通道幅相不一致、器件的热噪声等多种因素的影响,改进IFM系统中各MPD的UI、UQ输出不会是平滑的曲线,考虑到实际情况,仿真中对UI、UQ加入随机噪声,并假设信号噪声比SNR为10 dB.题设条件下改进IFM系统各MPD的UI、UQ通道输出如图4所示。

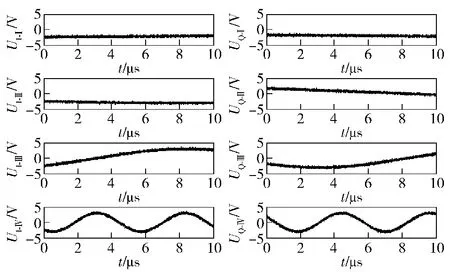
图4 4组UI、UQ通道输出值Fig.4 Output values of quad UIand UQchannels

3.2 ADC采样输出

然后,改进IFM系统在LFM信号检波包络整形脉冲的指示下,其ADC对其4组MPD的UI、UQ通道输出进行连续采样量化。设 ADC采样率为10 MHz,量化位数为5,对于实验LFM脉冲可得到100个采样值,如图5所示。

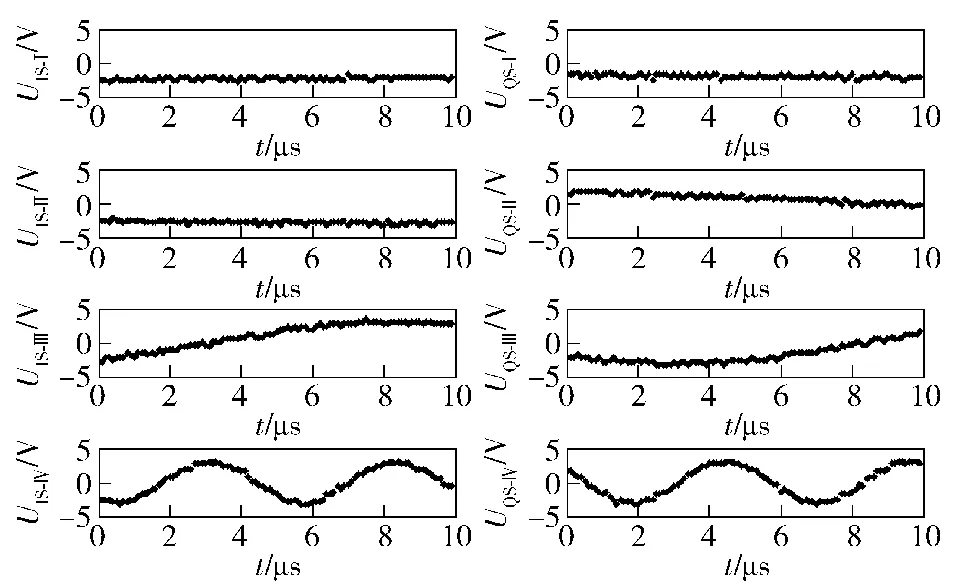
图5 4组UI、UQ通道采样值Fig.5 Sampling values of quad UIand UQchannels

3.3 频率模糊修正

依据图5和(3)式,连续计算LFM信号的采样频率值如图6(a)所示。应用2.2节中解模糊算法消除反正切模糊和频率模糊,如图6(b)所示。

图6 消模糊之前和之后频率值Fig.6 Frequency values after and before fuzzy clearness

3.4 线性回归去噪

模糊修正后Ⅳ支路输出精度较高的100个离散频率值。用线性回归[15]算法对这些离散频率值做平滑去噪处理,可得图7所示斜线。

图7 平滑去噪后的频率值Fig.7 Frequency values after noise smoothing

其中载频估计值 ^f0为4 001.1 MHz,调频斜率估计值 ^K为19.87 MHz/μs,与题设条件是比较接近的。由(21)式可计算其频率分辨力 Δfmin= 2.1 MHz;由(24)式得其调频斜率分辨力为ΔKmin= 0.21 MHz/μs2.

3.5 参数估计的误差分析

改变UI、UQ的信噪比SNR可得图8所示载频均方根误差、调频斜率均方根误差的变化情况。从图8可以看出,随着SNR的增加,估计误差逐渐减小;当SNR＞5 dB的情况下载频误差f0e＜2 MHz,调频斜率误差 Ke＜0.2 MHz/μs,满足 IFM系统对LFM信号的测量要求。

4 结论

由以上IFM对LFM信号的处理模型和仿真实验可以总结出改进IFM系统的4个特点:其一,改进运算量较小,因此计算速度快,便于实现;其二,能够获得LFM信号的频率特征,且其所得的载频和调频斜率具有一定的估计精度;其三,在一个脉冲内即可检测估计出LFM信号的载频和调频斜率,保留了IFM的实时性特点;其四,采用ADC代替极性量化器,并没有改变IFM的测量机理,因此也保留了瞬时带宽宽、动态范围大的特点。最后需要说明的是,改进IFM系统仍然可以检测普通雷达信号的频率特征,在这种情况下只需将普通雷达信号视为调频斜率为0的LFM信号即可。

图8 误差和信噪比的关系Fig.8 Relationship between error and signal-noise ratio

References)

[1] 王星.航空电子对抗原理[M].北京:国防工业出版社,2008: 109-115.

WANG Xing.Aeronautics electronic countermeasure prenciple [M].Beijing:National Defense Industry Press,2008:109-115. (in Chinese)

[2] Merrill S.雷达手册[M].南京电子技术研究所,译.3版.北京:电子工业出版社,2010:310-311.

Merrill S.Radar handbook[M].China Electronics Technology Group Ccorporation,translated.3rd ed.Beijing:Publishing House of Electronic Industry,2010:310-311.(in Chinese)

[3] 胡来招.瞬时测频[M].北京:国防工业出版社,2002.

HU Lai-zhao.Instantaneous frequency measurement[M].Beijing:National Defense Industry Press,2002.(in Chinese)

[4] 董晖,姜秋喜,毕大平.数字侦察接收机中的瞬时频率测量技术[J].电子对抗技术,2005,20(5):7-10.

DONG Hui,JIANG Qiu-xi,BI Da-ping.The technology of measuring instant frequency in digital reconnaissance receiver[J]. Electronic Warfare Technology,2005,20(5):7-10.(in Chinese)

[5] 何明浩.雷达对抗信息处理[M].北京:清华大学出版社, 2010:104-106.

HE Ming-hao.Radar countermeasure information processing[M]. Beijing:Tsinghua University Press,2010:104-106.(in Chinese)

[6] East P W.Fifty years of instantaneous frequency measurement [J].IET Radar,Sonar&Navigation,2012,6(2):112-122.

[7] Sandhyarani S,Kavith T.Design and implementation of DIFM algorithm in FPGA[J].Global Journal of Advanced Engineering Technologies,2013,2(3):83-88.

[8] Prasanthi P,Kumar P R,Ksingh A,et al.FPGA implementation of time frequency algorithm for intrapulse modulation recognition of RADAR signals[J].International Journal of Emerging Trends in Engineering and Development,2012,7(2):571-578.

[9] 王本庆,李兴国.LFM信号调频斜率的双正交 Fourier变换分析算法[J].电子与信息学报,2009,31(7):1620-1623.

WANG Ben-qing LI Xing-guo.Analysis algorithm to frequency rate of LFM signal based on biorthogonal Fourier transform[J]. Journal of Electronics&Information Technology,2009,31(7): 1620-1623.(in Chinese)

[10] 朱文涛,郑纪彬,苏涛,等.线性调频连续波信号的检测和参数估计[J],电子与信息学报,2013,35(7):1562-1568.

ZHU Wen-tao,ZHENG Ji-bin,SU Tao,et al.Detection and parameter estimation of linear frequency modulation continuous wave signal[J].Journal of Electronics&Information Technology, 2013,35(7):1562-1568.(in Chinese)

[11] 朱健东,赵拥军,唐江.线性调频连续波信号的周期分数阶Fourier变换检测与估计[J],电子与信息学报,2013,35(8): 1827-1833.

ZHU Jian-dong,ZHAO Yong-jun,TANG Jiang.Periodic FRFT based detection and estimation for LFMCW signal[J].Journal of Electronics&Information Technology,2013,35(8):1827-1833.(in Chinese)

[12] 马宁,王建新,董宁斐.基于正交匹配追踪的欠采样LFM信号参数估计[J].电子与信息学报,2013,35(8):1888-1893.

MA Ning,WANG Jian-xin,DONG Ning-fei.Parameter estimation of sub-sampling LFM signal based on orthogonal matching pursuit[J].Journal of Electronics&Information Technology, 2013,35(8):1888-1893.(in Chinese)

[13] 刘昊晨,梁红.线性调频信号参数估计和仿真研究[J].计算机仿真,2011,28(2):157-159.

LIU Hao-chen,LIANG Hong.Estimation and simulation study of LFM signal parameters[J]. ComputerSimulation,2011, 28(2):157-159.(in Chinese)

[14] 孙志国,陈晶,申丽然,等.基于TSLPFT1-FFT的线性调频信号参数估计方法[J]电路与系统学报,2011,16(5):24-29.

SUN Zhi-guo,CHEN Jing,SHEN Li-ran,et al.Parameters estimation of linear frequency modulation signal based on TSLPFT1-FFT[J].Journal of Circuits and Systems,2011,16(5):24-29.(in Chinese)

[15] 顾基发.运筹学[M].北京:科学出版社,2011:245-246.

GU Ji-fa.Operation research[M].Beijing:Science Press,2011: 245-246.(in Chinese)

Analysis of LFM Signals and Improvement of IFM System

WANG Hong-xun1,2,WANG Shi-yan2,3,WANG Xing2,WANG Hong-wei2
(1.School of Automation,Northwestern Polytechnical University,Xi'an 710072,Shaanxi,China; 2.Aeronautical and Astronautical Engineering College,the Air Force Engineering University,Xi'an 710038,Shaanxi,China; 3.32th Unit,93286th Air Forces,Shenyang 110141,Liaoning,China)

Frequency is one of the key features of radar signals,which is extracted in real-time by an instantaneous frequency measurement(IFM)system in electronic warfare receivers used for RWR/ESM. Linear frequency modulation(LFM)signal is an important signal type and used widely in radar,and its frequency characteristics could not be detected by traditional IFM system.A novel technique is proposed based on improved IFM system for LFM signal feature detection,and a mathematical model of LFM signal passing through IFM system is established based on the operating principle of IFM system.The frequency resolving capacity and the minimum detectable frequency modulation slope are discussed.In the improved IFM system,a phasing detector signal is used as the effective indicating signal of sampling to extract the time of arrival(TOA)and pulse width(PW)features.The analog-digital converters(ADC)instead of polarity quantizer of traditional IFM system are used to sample continuously the outputs of the orthogonal channels.The fuzzy clearness and linear regression algorithms are used for noise smoothing and evaluating the carrier frequency and the frequency modulation slope of LFM signal.Simulation results show that theimproved IFM system could extract the LFM signal features in an LFM pulse with higher accuracy,and retains the advantages of original IFM system.

radar engineering;instantaneous frequency measurement;linear frequency modulation; fuzzy clearness;linear regression

TN971+.1

:A

:1000-1093(2014)08-1193-07

10.3969/j.issn.1000-1093.2014.08.009

2013-06-18

国家“863”计划项目(2010AA80910514C)

王洪迅(1977—),男,讲师,博士后。E-mail:whxwhxwhx@126.com