一种基于四叉树的数字图像压缩算法*

陈云鹏 谢志成 郑创伟 陈宇辉 曾宇鹏 杜雪清

(1.华中科技大学计算机学院 武汉 430074)(2.深圳报业集团 深圳 518009)

一种基于四叉树的数字图像压缩算法*

陈云鹏1谢志成2郑创伟2陈宇辉2曾宇鹏2杜雪清2

(1.华中科技大学计算机学院 武汉 430074)(2.深圳报业集团 深圳 518009)

基于四叉树的数字图像压缩算法是一种利用四叉树结构对图像中平滑区域进行压缩编码的技术。而现有的压缩算法由于存在诸多缺陷,使得其效果很难与诸如Jpeg2000的主流压缩算法相比拟。论文基于现有的四叉树分割算法,提出了一种高效的编码方式来记录四叉树的结构信息,同时引入了泰森多边形方法和自然邻点插值法来解决四叉树重构时的平滑问题。实验结果表明,该算法在尽可能小的失真前提下,最大限度地保留了图像的细节信息,且具有较高的压缩比,其整体效果可以与Jpeg2000比拟。

图像压缩; 四叉树; 四叉树分解; 多边形插值; 图像压缩编码

Class Number TP391

1 引言

随着互联网的普及和多媒体技术的快速发展,数字图像正以指数级的速度增长。如在线图像分享站点www.fichr.com仅至2009年,分享上传的图片数量就已突破了40亿张[1]。如何有效地压缩数字图像,去除数据中的沉余信息,减少数据存储空间实现数字图像的海量存储与快速传输,已成为数字图像处理领域中一项重要问题。由于在实际应用中,所接触到的图像其大部分区域都是平滑的,只有部分边缘区域灰度值剧烈变化,因此一种较好的图像压缩方式就是将图像不断分割成一块块平滑区域,之后利用算法对每个区域进行编码。由于高度的边缘信息被分割为许多平滑的小区域,因此除了需要保存其颜色信息,还需要记录其结构信息。

针对这一问题,一种有效解决办法是利用四叉树来表示这些小区域的结构位置信息。基于四叉树的分解算法诸如文献[2～6],其主要思想是将图像分块成许多小块,每一个小块作为四叉树的一个叶子节点以灰度值表示,或者是由一个特征向量所表示。但这些算法均存在压缩率较低,难以适应大尺寸图像等限制,使得其压缩效果很难与现有的主流压缩算法相比拟。

本文基于现有的四叉树分割算法,提出了一种高效的编码方式来记录四叉树的结构信息,同时引入了泰森多边形方法和自然邻点插值法来解决四叉树重构时的平滑问题。实验结果表明,本文提出的算法可以有效解决图像压缩问题,其在尽可能小的失真前提下,最大限度地保留了图像的边缘信息,同时达到了较高的压缩比,总体效果可以与Jpeg2000比拟。

2 图像压缩算法

2.1 图像编码系统

2.1.1 四叉树分解算法

四叉树分解将原始图像逐步分成小块,操作的目标是将具有一致性的像素分到同一小块中,通常这些小块都是方块[7],只有少数情况分成长方形或三角形[8]。一般来说,对一幅任意尺寸的图像进行四叉树分解前,需对图像进行归一化操作,通过简单的缩放使得图像变为方形,且像素点的个数是2的整数次幂时,以便四叉树分解。

进行四叉树分解的具体过程是:首先把原始图像视为原始子块,如果当前子块满足一致性标准,则存储该整体子块的像素值;否则将方形的原始图像继续分成四个大小相同的方块,再视每一子块为一原始图像重复上述过程,直至所有子块均满足一致性标准才停止。现有的一致性检验标准很多,如QRH[5]和纹理特征等。本文采用标准差作为一致性检验标准,该方法有算法复杂度低、算法简单、可以有效地表示子块中图像的边缘信息等诸多优点,其分割效果如图1所示。

图1 四叉树分解示意图

2.1.2 四叉树的结构编码

在四叉树的存储中,除了要保存叶子节点的颜色信息,还需要保存四叉树本身的结构信息。如在指针形式中,每一结点需4个或5个指针场。在三元组(L,X,Y)存储形式中,对每个结点需要指出它所在的层次L及它在该层中所处的位置(X,Y)。但是该方法需要的存储空间过大,因此文献[2～3]中,作者提出了两种对二值图像进行编码的方式,但尽管该方法可以推广至多值图像,其实现需要较繁琐的位操作且需存储每一结点的地址;在文献[4]中作者提出一种改进方法,即每个结点用一个字节表示灰度,并设一个结点属性标志位的方式节省存储空间,但仍需要至少半个字节来存取位置信息。

本文受到文献[5]的启发,通过对四叉树的子结构进行编码,以达到节省存储量的效果。对于每两次四叉树的分解,可以使用一组二进制数进行编码(D0,D1,d1,d2,d3,d4),如图2(b)所示。D0代表当前块是否分解,若分解则为1,否则为0;如果D0=1,那么第二个D1则代表该4x4的块是否继续分解成至少8x8的块,或者到此为止。如果D1=1那么d1,d2,d3,d4则表示图中按行序编号的子块“1”、“2”、“3”、“4”是否再继续分解成另4x4的块。文献[5]中作者指出,该方法平均每个结点的颜色信息只需0.003bit来存储其位置信息。

表1 编码串示意表

图2 文献[5]所给分解及编码算法

尽管该方法可以高效保存四叉树的位置信息,但由于其模板所能代表的结构类型有限,树的深度最多只能达到三层,这使得其并不使用的大尺寸图像的压缩。为了弥补这一不足,本文对其进行了改进,使其可以表示两次以上的四叉树分解,其具体思想如下:

以进行三次四叉树分解为例:首先对当前块进行一般的四叉树分解,直至全部分解完毕,之后,对每两次分解使用一次上述编码规则,如:在图3中Layer1中的模块其(D0,D1,d1,d2,d3,d4)分别对应110011。但,其中d1,d2,d3,d4不再表示其是否是叶子节点,而表示其是否存在子树:若为1,则存在4棵子树,即该节点是另外4棵树的根。对于一个需要进行至少3分解(深度为4)的图片,编码过程如图3所示,其最终编码为110011000100000。

完成对树结构的编码信息后,只需进行简单的层次遍历,即可将其转化为物理存储形式。且在实际编码时,由于最后一层往往全部为0,因此可以不存储最后一层的结构信息(因为前一层的信息已经足够表示最后一层的信息了),以此进一步压缩存储空间。实验表明,对于一个需要两次以上分解的图像,平均每个结点的颜色信息只需0.03bit来存储其位置信息;而对于一个仅需两次以下分解的图像,该方法可以退化为原有算法,即平均每个结点的颜色信息只需0.003bit来存储其位置信息。

图3 树的结构编码示意图

2.2 图像解码系统

2.2.1 解码部分

图像的解码包含二进制译码和树的结构重构这两部分。二进制译码即读取四叉树位置信息的二进制代码,根据事先定义好的模板(字典)查找,对连续的二进制位进行分割、提取并将其保存为诸如序号的存储形式,使其与事先定义好的模板(字典)相关联,其具体过程如图4所示。树的结构重构即根据二进制译码结果,利用相应模板的结构信息,利用按层遍历或先序遍历等方式重构树的结构信息,使其形成四叉链表等易于操作存储结构,以便于后期对图像的重构,期间需利用栈和列队或递归过程。

总体思路可简单描述为:首先将二进制位置信息进行译码,使其与相应的子树结构相对应。其次,重构四叉树的结构:通过先验知识计算最初曾的节点数,依次读取最初层的所有节点,计算其子树的个数,作为下一层读取的结点个数,如此迭代。

图4 二进制译码过程示意图

2.2.2 图像重构

“图像重构”即根据恢复出的四叉树结构信息,利用四叉树的叶子上的颜色信息或特征向量,恢复原始图像的过程。简单来说,它是对图像分解的一个逆过程。现有的插值算法多是基于均匀值块方式,即将整个正方形区域填充为单一颜色(纯色),其会产生明显的马赛克,因此其视觉效果并不理想。而插值法(又称“内插法”),是利用函数f(x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f(x)的近似值[10]。其具有计算精度高,能产生较清晰光滑的图像并不丢失其边缘信息的特点,并广泛应用到各种图像缩放算法中。然而数字图像处理中现有的插值方法,诸如最邻近插值、线性插值、双线性插值均要求像素成点阵的形式分布,而叉树分解出来的块大小不一分布上也没有规律,因此不适用。

本文受到地球科学的启发,引入了泰森多边形及其插值算法来解决四叉树分解图像的插值问题,如图5所示。

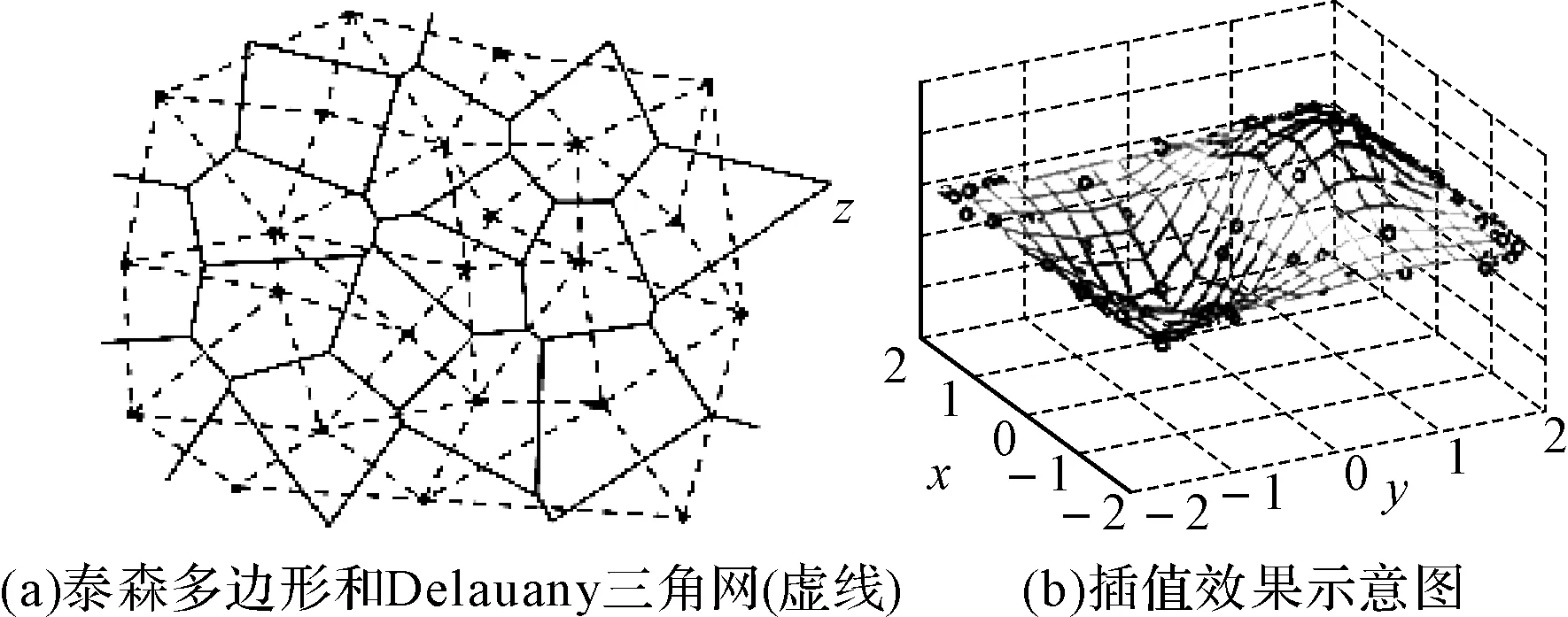
图5 泰森多边形及其插值算法

泰森多边形最早是由荷兰气候学家A.H.Thiessen提出的一种根据离散分布的气象站的降雨量来计算平均降雨量的方法。但其实际应用范围却十分广泛,凡是涉及定性分析、统计分析、邻近分析等的问题均可以使用基于泰森多边形的方法解决。现有的基于泰森多边形的插值方式有Kriging、Nearest Neighbor、Natural Neighbor等。其中Kriging方法,相比于后两种方法,算法复杂度较高,不适合于对数据点较密的数字图像进行插值。本文分别采用了最邻近法和自然临近点法对四叉树图像进行重构。

1) 最邻近法

最近邻点插值法(NearestNeighbor)又称泰森多边形方法,是由荷兰气象学家A.H.Thiessen提出的一种分析方法。最初用于从离散分布气象站的降雨量数据中计算平均降雨量。实际上,最近邻点插值的一个隐含的假设条件是任一网格点p(x,y)的属性值都使用距它最近的位置点的属性值,用每一个网格节点的最邻点值作为待插值的节点值[11]。

尽管理论上最邻近法仍会存在块与块之间没有过度的问题,但针对四叉树分解图像重构这一问题,由于点与点之间的间隔很小,其仍然可以达到很好的效果,如图6所示。

图6 应用最邻近点插值法后效果图

2) 自然临近点法

自然邻点插值法(NaturalNeighbor)是对最近邻点插值法的一种改进算法,它克服了最邻近点法中块与块之间无过渡的问题,达到了更佳的插值效果。其广泛应用于一些研究领域中,它的基本原理是对于一组泰森多边形,当在数据集中加入一个新的数据点(目标)时,就会修改这些泰森多边形,而使用邻点的权重平均值将决定待插点的权重,待插点的权重和目标泰森多边形成比例[12]。实际上,在这些多边形中,有一些多边形的尺寸将缩小,并且没有一个多边形的大小会增加。同时,自然邻点插值法在数据点凸起的位置并不外推等值线(如泰森多边形的轮廓线)。针对四叉树的图像重构问题,其插值结果如图7所示。

图7 应用自然近点插值法后效果图

3 复杂度分析

3.1 编码部分的复杂度

编码部分包括:标准四叉树分解算法和本文提出的四叉树结构编码方式,其中标准的四叉树分解算法的时间复杂度为O(n^2),四叉树的结构编码的时间复杂度为O(n),因此编码部分的时间复杂度为O(n^2)。

3.2 解码部分

图像的编码系统包括:译码重构部分和图像重构部分,译码部分的时间复杂度为O(n),树的结构重建的时间复杂度为O(n^2);图像重构部分的时间复杂度根据所选算法的不同而有所差异,其中均匀快法的时间复杂度为O(n^2),最邻近法的时间复杂度为O(n^2),而自然临近法的时间复杂度为O(n^3)。

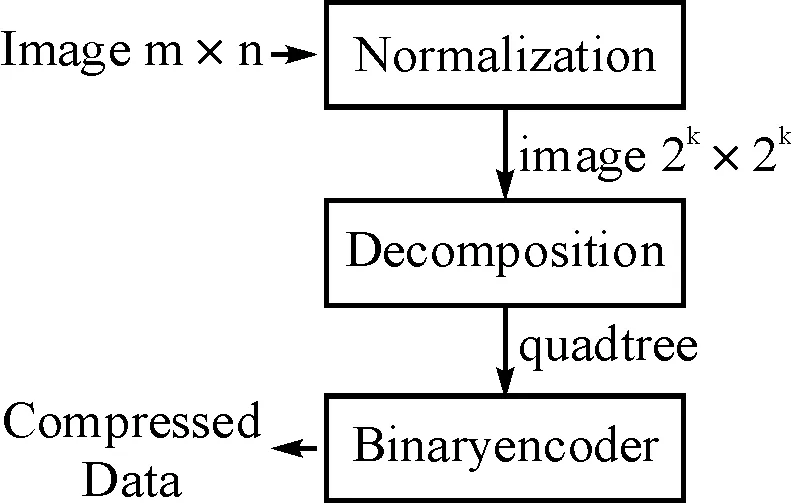
(a)编码系统结构框图

(b)解码系统结构框图

4 实验结果

4.1 实验设计

本实验分为两个部分:实验1测试图像的有损压缩性能,分别对彩色图像和灰度图像进行有损压缩测试;实验2测试图像在无损压缩的情况下的压缩情况。

实验所使用的测试图像集为Standard_Test_Images[13];其中利用释义峰值信噪比(PSNR)、均方误(ERMS)作为定量评价标准,人眼视觉感受作为定性评价标准。

4.2 有损压缩性能测试

本实验测试图像的有损压缩性能,灰度图像的测试结果如图9所示;彩色图像的测试结果如图10所示;表2列出了上述所有测试图像的具体参数与有损测试结果。

图9 灰度图像压缩效果

通过对图像的观察可以看出,本文提出的图像压缩算法均能有效地压缩图像并尽可能地保留了图像的内容,其中:均匀块法恢复的图像有马赛克的感觉,而另外两种插值算法恢复出的图像即不失细节纹理又十分平滑,视觉效果更佳。

图10 彩色图像压缩效果

图11和图12分别给出lena_gray_512.tif的释义峰值信噪比(PSNR)、均方误(ERMS)曲线,横轴为压缩率(bit/pixel)。可以看出本文提出的算法其各项指标可以与Jpeg2000比拟,其中均匀快法(Blocks)的效果最好,而插值法(Nerarest)的效果较差,这主要是由于插值曲线不完全拟合造成的。

图11 PSNR测试结果曲线

图12 ERMS测试结果曲线

文件名尺寸BMP压缩后压缩率cameraman.tif512×512256kb18kb0.0708woman_darkhair.tif512×512256kb6kb0.0246lena_color_512.tif512×512768kb52kb0.0714mandril_color.tif512×512768KB253kb0.3333

4.3 无损压缩性能测试

本实验测试图像的无损压缩性能,测试所用图像与实验1相同。表3列出了上述所有测试图像的具体参数与无损压缩测试结果。

表3 无损压缩数据表

从表3可以看出,本文提出的四叉树结构编码规则可以高效地保存四叉树的结构信息,同时使得位置信息的空间占用率尽可能的小。即使在无损压缩这种四叉树结构最复杂的情况下,仍能使得空间信息占用率小于3%。

5 结语

本文介绍并分析了现有的几种四叉树压缩算法,分别指出了其优缺点,并在此基础上,提出了一种高效的编码方式来记录四叉树的结构信息,该编码方式可以高效保留四叉树的结构信息,具有算法实现简单,算法复杂度低等优点;此外,本文还将泰森多边形方法和自然邻点插值法引入到发杂图像的重构的问题上来,以此解决四叉树分解图像重构时的平滑问题。

实验结果表明,本文提出的算法可以有效解决图像压缩问题,其在尽可能小的失真前提下,最大限度地保留了图像的细节信息,同时也达到了较高的压缩比,总体效果可以与Jpeg2000比拟。然而,泰森多边形方法和自然邻点插值法的引入使得算法的时间复杂度为O(n^3),使得该算法并不适用于较大的图像压缩,同时也使其难以应用于实时的图像压缩系统中。因此,如何进一步降低算法的时间、空间复杂度将成为下一步的工作重点。

[1] Wang J Z, Geman D, Luo J, et al. Real-world image annotation and retrieval: An introduction to the special section[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on,2008,30(11):1873-1876.

[2] Gargantini I. An effective way to represent quadtree[J]. Comm. of ACM,1982(12):905-910.

[3] Kawaguchi E, Endo T. On a method of binary-picture representation and its application to data compression[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on,1980(1):27-35.

[4] 高蕴健,李介谷.四叉树与数据压缩[J].机器人,1987,9(4):38-42.

[5] Keissarian F. A new quad-tree segmented image compression scheme using histogram analysis and pattern matching[C]//Computer and Automation Engineering(ICCAE), 2010 The 2nd International Conference on. IEEE,2010,5:694-698.

[6] El-Harby A A, Behery G M. Qualitative image compression algorithm relying on quadtree[J]. Mansoura University, Faculty of Science, Math. Dept., ICGST-GVIP,2008,8(3):2-3.

[7] 过洁,潘金贵.一种新的基于线性四叉树的图像分割算法[J].系统仿真学报,2009(1):54-55.

[8] 朱志良,赵玉丽,于海.基于像素分布与三角形分割的快速分形图像压缩算法[J].计算机应用,2010(2):337-340.

[9] 徐雨明,文双春.数字图像插值算法的分析与实现[J].福建电脑,2007(1):94-94.

[10] 刘慕溪.数值分析中常见插值法的浅析[J].科技致富向导,2011(24):33-33.

[11] 李庆扬,关治.数值计算原理[M].北京:清华大学出版社有限公司,2000.

[12] 沈剑华.数值计算基础[M].上海:同济大学出版社,2004,8.

[13] "Standard" test images[EB/OL]. http://www.imageprocessingplace.com/root_files_V3/image_databases.htm.

Image Compression Based on Quad-tree Coding with Voronoi-Interpolation

CHEN Yunpeng1XIE Zhicheng2ZHENG Chuangwei2CHEN Yuhui2ZENG Yupeng2DU Xueqing2

(1. School of Computer Science and Technology, Huazhong University of Science and Technology, Wuhan 430074) (2. Shenzhen Newspaper Group, Wuhan 518009)

Quadtree-based image compression technique is a typical method which aims to exploit the redundancy in an image such that the smaller number of bits can be used to represent the image while remaining detail information. However, most of existing approaches to this problem do not work well due to its own limitations. Here a new approach to code quad-tree decomposed Image with a novel codebook and then be reconstructed by voronoi interpolation is described that provides a "satisfying" visual quality comparing with Jpeg2000.

image compression, quadtree, quadtree decomposition, voronoi-interpolation, image coding

2014年5月5日,

2014年6月25日 作者简介:陈云鹏,男,研究方向:数字图像处理,高维数据索引,机器学习,图像压缩。谢志成,男,硕士,研究方向:信息系统管理。郑创伟,男,研究方向:信息系统管理。陈宇辉,男,硕士,研究方向:微电子设计。曾宇鹏,男,硕士,研究方向:计算机网路。杜雪清,女,研究方向:信息系统管理。

TP391

10.3969/j.issn1672-9730.2014.11.010