关于实变函数教学中的一些注记
苏先锋,秦喜梅,李晓萌
(1.淮北师范大学 信息学院,安徽 淮北 235000;2.巢湖学院 数学系,安徽 合肥 238000)
实变函数课程是数学专业本科教学教育阶段最重要的专业必修课程之一,是数学分析的后继课程[1-4],也是学生学习泛函分析、概率论与随机过程、分形几何等现代数学的基础,在数学中起到承上启下的桥梁作用.同时,实变函数以逻辑的严谨性,定理及概念的抽象性,证明过程的复杂性及证明中要使用大量的构造,使得实变函数的名声不佳,学生在学习的时候常会感到困难和困惑,学习的兴趣也随着课程学习的深入而消失殆尽,最后成为深入学习数学的障碍.很多教师就实变函数的教学做了大量有益的研究,如杜波[5]讨论构造性方法在实变函数教学中的应用,姜建功[6]和倪仁兴[7]探讨实变函数与数学分析课程的密切关系,陈亮[8]研究实变函数教学对学生科研能力有着积极的作用,刘鑫[9]讨论反例在实变函数教学中的应用.本文结合在实变函数教学中的体会,旨在如何提高课堂的教学效果和学生学习的兴趣与信心等方面做一些探讨.
1 教学中对相关内容做适当的拓展
在教学中,首先出现实变函数与其他课程割裂,课堂上很少提及与其他课程的联系.其次,与现实生活脱节,似乎实变函数这门课程与生活无关,看不见摸不着,是纯理性思维的结晶.实变函数的部分概念和结果貌似都违背人们的认知,像是“帽子里跑出了一只兔子”[4]..因此,与其他课程建立联系是有必要的,不仅能使学生体会到实变函数这门课程的重要性,感受其与生活密切相关,也展现数学的魅力.
如学习Lebesgue测度后,课堂上可以继续介绍概率测度,建立实变函数与概率论的关系,为概率论的学习提供理论支持,提高学生学习兴趣,感受到学习实变函数的重要性,从思想上重视该课程.同时,对教师也提出更高的要求,讲授实变函数课程必须充分掌握概率论的本质,从而建立起两门课程的联系.
文[4]中介绍Cantor 三分集的精细机构和特殊性质及分形几何的一些知识,如科赫曲线,谢尔宾夫斯基地毯等分形机构,在课堂上和学生分析魔方的结构特点,构建一个分形结构.即将单位变长的魔方进行构造,魔方有27块小立方体,去掉中间小立方体,再继续将剩下26块小立方体看成新的魔方,去掉中间小立方体,如此一直下去,最终我们得到了一个分形结构,我们称之为“魔方分形”.可以与学生一起讨论魔方分形结构的Hausdorff 维数,体积,面积及其与Cantor 三分集之间的关系.介绍分形几何时,利用多媒体播放《Hunting the Hidden Dimension》短片,介绍了分形几何的产生及其在服装设计、手机制造、电影特效、气候研究、医学等方面的应用,让学生体会到数学在生活中无处不在,增强学生的学习兴趣,提高课堂的教学效果.
2 教学中兴趣点的构建
教学中兴趣点的构建与合理利用,有利于教学效果和学生学习兴趣的提高.在教学中如何构建好兴趣点显得尤为重要,兴趣点要求通俗易懂,最起码对数学专业的学生应该没有障碍.兴趣点有以下几个方面的作用.(1)可以活跃课堂气氛;(2)可以引导学生深入思考;(3)对概念和结论的理解更加透彻;(4)增强学生的学习兴趣与信心,提高教学效果.兴趣点可从数学故事,数形结合,反例,类比法等方面来构建.
2.1 兴趣点之数学故事
实变函数中可以寻找或构建一些简单的数学故事说明问题.常见的有“住店问题”,“还钱问题”,“乡村理发师问题”等数学故事.如”住店问题”,有个旅馆有可数间房间,已经住满了旅客,现在又来一名旅客需要住店,该如何安排?这个例子学生可以深刻体会可数集与有限集的区别.如“还钱问题”,介绍Lebesgue积分与Riemann积分的区别,Lebesgue自己曾经给出了类似的比喻,如要还别人的钱,从口袋里掏出来不同面值的钞票,一种方法即是一张张钞票按面值加起来得出钱数,另一种方法就是把相同面值的钞票数出来,然后把不同面值的总额度加起来得出钱数.前者为Riemann积分思想,后者为Lebesgue积分思想.
2.2 兴趣点之数形结合
实变函数教学中,可以借助图形图像证明结论、说明概念,使问题简单化,概念理解深刻化.如在集合论中,利用维恩图说明集合的运算关系,通过图像来证明集合对等.在证明两个可测集的并集是可测集,验证卡氏条件时,文献[1]中利用维恩图来辅助证明,给学生直观的认识,降低证明的难度.阶梯函数为简单函数,可以说明Riemann积分与Lebesgue积分的区别.
例如:
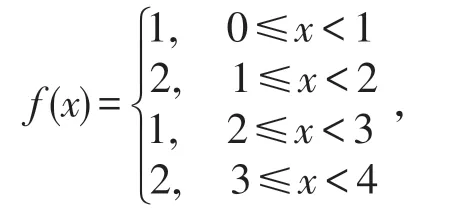
f(x)为简单函数,图像如图1.
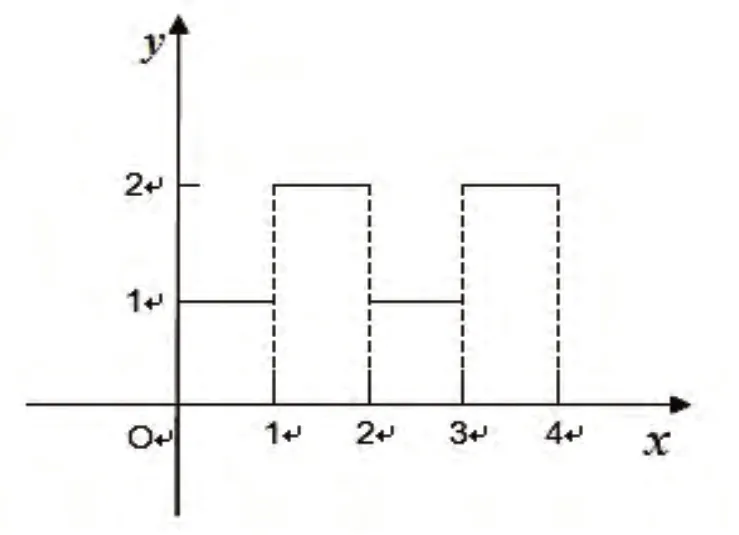
图1 f(x)函数图像
则
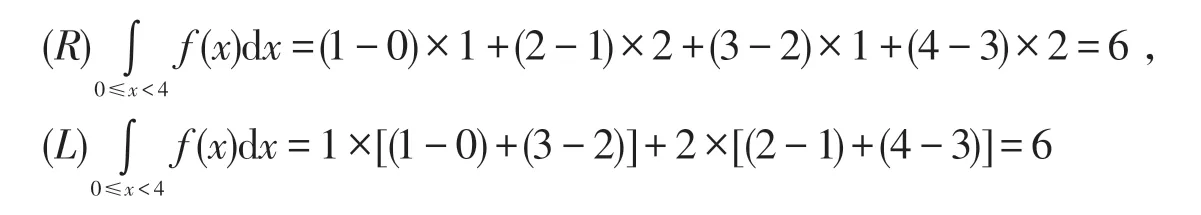
此例实质上与Lebesgu“e还钱问题”有相似的效果.
2.3 兴趣点之反例
反例在教学中恰当的应用,可以达到举一反三的效果.反例可以对似是而非的问题给以否定的回答,说明结论的条件不可或缺.很多文献中都举出很多反例来说明问题和结论.如简单函数是可测函数,简单函数似乎Riemann可积的.事实上,我们知道狄利克雷函数是简单函数,但是狄利克雷函数Riemann不可积的,所以简单函数也未必Riemann可积.叶果罗夫定理中的条件,文[4]给出反例说明定理的条件是不可或缺.可以通过简单的反例来说明概念的本质.反例是实变函数教学中的重要环节之一,有利于学生对概念或结论有深刻的认识,提高教学效果.
2.4 兴趣点之类比教学法
类比教学法是教学中最常用的教学方法之一,特别在实变函数教学中最为特别,因为实变函数是数学分析的后续课程,实变函数与数学分析有着深厚的关系.实变函数的研究就是因为Riemann积分存在着一些缺陷而兴起的.如狄利克雷函数Riemann不可积,极限与积分交换次序条件要求严格等.在实变函数中,这些问题都得到解决或条件得以放宽.与数学分析进行类比,可以达到温故而知新的效果.与数学分析的内容进行比较,不仅能降低课程难度,让学生有学习的成就感,提高学生学习兴趣和学习信心.
兴趣点可以从很多方面去构建和发现,如实变函数的一些特别的条件语言描述,形象地说明Lebe⁃sgue积分优于Riemann积分.思考题同样可以很好的利用,如我们学习Cantor三分集的结构,可以让学生思考构建类似三分集的五分集,即单位长度的五等分,去掉第二段和第四段,剩下三段继续五等分,再去掉其中第二和第四部分,如此下去.得到相关的性质.课堂上,经常设置一些思考题,让学生通过一定努力就可以解决的问题,提高学生分析问题的能力.
3 结语
在教学中需要我们不断的总结,讲授一些与其他课程或生活的联系和构造一些兴趣点,可以提高教学效果,改变实变函数的教学现状.同时,帮助学生提高学习实变函数课程兴趣与信心,也为学生后续学习打下良好基础.
[1]周民强.实变函数论[M].北京:北京大学出版社,2001.
[2]胡适耕.实变函数[M].北京:高等教育出版社,2000.
[3]夏道行.实变函数论与泛函分析[M].2版.北京:高等教育出版社,1995.
[4]程其襄.实变函数与泛函分析[M].3版.北京:高等教育出版社,2010.
[5]杜波.构造性方法在实变函数教学中的应用[J].高等数学研究,2012,15(4):89-90.
[6]姜建功.Lebesgue积分在数学分析中的应用[J].孝感学院学报,2001,30(6):18-20.
[7]倪仁兴.浅议实变函数与数学分析间的关系[J].绍兴文理学院学报,2001,21(3):93-97.
[8]陈亮,许绍元.在实变函数课程教学中培养学生科研能力的体会[J].淮北煤炭师范学院学报:自然科学版,2003,24(2):53-55.
[9]刘鑫.反例在实变函数中应用[J].高等数学研究,2009,12(4):117-123.

