结合空间金字塔局部特征的谱匹配算法

江 源，鲍文霞，吴祖恒

（安徽大学 电子信息工程学院，安徽 合肥 230601）

图像匹配是计算机视觉的核心研究课题，并广泛应用于图像拼接、运动分析与跟踪、目标分类与识别以及三维结构重建等［1］.近年来，基于谱分解的图像匹配算法成为研究热点.Scott和Longuet-Higgins等［2］最早将谱分解的方法应用到图像匹配中，根据两幅图像特征点之间的高斯加权关系构造邻接矩阵，并对其进行奇异值分解获取图像特征点之间的对应关系.但该算法对于具有较大旋转、缩放等变换的图像匹配精度迅速下降.为了提高匹配的精度，Shapiro和Brady等［3］分别利用每一幅图像内部特征点之间的高斯加权来构造邻接矩阵，Pilu［4］在前两种算法的基础上，改进了邻接矩阵的度量方式，加入了灰度相似性度量，从而提高图像的匹配准确性.但是由于其选择了固定的大小和方向的图像窗，易受到噪声、尺度、旋转等变换的影响.针对上述方法的不足，Yue等［5］利用SIFT特征的归一化互相关度量方式重构邻近矩阵，Tang等［6］利用特征点之间距离相似性构造Laplace矩阵，梁等［7］结合局部形状上下文特征作为度量方式构造Laplace矩阵，都是通过谱分解实现特征点的匹配，这些算法在一定程度上提高了图像在较大尺度、旋转和光照等变换时的鲁棒性.

基于谱分解的匹配算法简单高效，并具有最近邻、排异性和相似性的原则.但谱匹配算法中邻接矩阵度量方式对匹配结果影响较大，因此，本文提出了一种空间金字塔局部特征描述，该特征描述在性能上优于 SIFT［8］、GLOH［9］、CS-LBP［10］等描述，并以该局部特征描述作为特征点之间相似性的度量方式，重构邻接矩阵，通过谱分解获取特征点匹配关系.

1 改进的CS-LBP特征值

CS-LBP描述子是在局部二元模式（Local Binary Pattern，LBP）［11］描述子基础上，为了减少二进制模式，而仅通过比较基于中心对称的两个邻域点的灰度值来进行编码的纹理描述子.为了使特征描述进一步具有旋转不变性，本文通过对CS-LBP方法进行修正来计算特征值.

设某个特征点对应的局部特征区域规范化后为ω={x1,x2,...,xn}，I(x)表示点x的亮度值.xi为区域ω中的任一采样点，选取点xi和特征点x的连线与圆周的两个交点距离特征点较近的点作为第一个采用点x0，然后沿逆时针方向在圆周上均匀地采样其余的N-1个点，如图1所示.则xi的特征值为：

其中xi+(N/2)是关于xi中心对称的点，T是一个阈值.

图1 N=8时的特征值计算Figure 1 Diagram of feature value calculation for N=8

2 空间金字塔局部特征描述

由式（1）可以看出，基于中心对称的两个邻域点的灰度值的差被表示为一个N2 比特的二进制数，这样会得到种不同的模式，即

引入空间金字塔对局部特征区域进行多尺度划分，l∈L表示划分的尺度，则在尺度为l的空间上会得到2l个子区域，如图2所示.在每个尺度下每个子区域中统计每一种编码模式出现的频率，于是在l尺度空间上得到K=d×2l维的向量集：χl(x)=(χl1,χl2,...,χlK)，其中

NUMk为第k个子区域的像素数目.αl为l尺度空间上分配的权值，当l=0 时；当l＞ 0 时，，即划分越密集权重越大.χl(k,h)表示第k个子区域中特征值为第h种模式的统计值.

将每个尺度得到的特征向量进行组合，得到最终的空间金字塔局部特征描述向量：χ(x)=(χ1(x),χ2(x),...,χL(x)).向量总的维数为：

图2 局部特征区域划分Figure 2 Division of local feature region

3 谱分解匹配算法

相似性度量是用来描述图像特征之间的相似程度，它通常使用距离函数或者匹配代价函数计算得出［12］，本文利用χ2距离来度量空间金字塔局部特征描述向量的相似性，并构造邻接矩阵.

给出两幅不同条件下的图像I1和I2，设它们分别含有n个待匹配的特征点.利用χ2距离来度量特征点x和y之间局部特征描述向量的相似性［12］：

由特征点构造的赋权完全图对应的高斯加权邻接矩阵定义如下：

其中，参数σ控制着匹配点之间的变化范围，当σ较小时，产生的匹配在局部较小的邻域内；当σ较大时，则允许匹配点对之间有较大的距离变化.

对邻接矩阵G进行SVD分解得到：

其中，D为对角矩阵.根据Scott算法［2］，通过式（7）计算得到匹配矩阵P：

E为矩阵D对角线上的非零元素置1得到的.匹配矩阵P的行向量和列向量分别表示图像I1和图像I2的特征点的特征信息.若Pij是匹配矩阵P的第i行和第j列的最大值，那么图像I1的第i个特征点和图像I2的第j个特征点相匹配，否则不匹配.

本文结合空间金字塔局部特征的谱匹配算法步骤总结如下：

（1）利用Hessian-Affine方法［9］检测特征点及特征区域；

（2）计算特征点的空间金字塔局部特征描述；

（3）按公式（5）构造特征点之间的高斯加权邻接矩阵；

（4）对邻接矩阵进行谱分解并获取特征点之间的匹配关系.

4 实验结果及分析

首先，为了验证本文给出的空间金字塔局部特征描述算法的性能，采用［13］中提供的数据集序列图像，分别用SIFT、GLOH、CS-LBP以及我们提出的算法对图像特征进行描述，计算各特征描述之间的欧式距离，并以最简单的最近邻、次近邻距离比作为度量进行匹配，最后采用recall—1-precision 准则［14］来对特征描述的性能进行评价：

图3为模糊变换图像序列，包含5帧图像（这里只列出了第1帧和最后一帧），将第1帧作为参考图像，其他4帧和参考帧进行匹配，结果如图5中的（a）、（b）、（c）以及（d）所示.图4为两幅光照变化图像，如图5中的（e）为其相应的匹配性能结果.从实验结果可以看出，本文给出的特征描述算法对于模糊、光照等变化较大时的图像在性能上明显优于SIFT、GLOH、CS-LBP算法.

图3 Bikes（模糊变换）图像序列Figure 3 Image sequences of bike（blur transform）

图4 光照变换图像Figure 4 Images of illumination transform

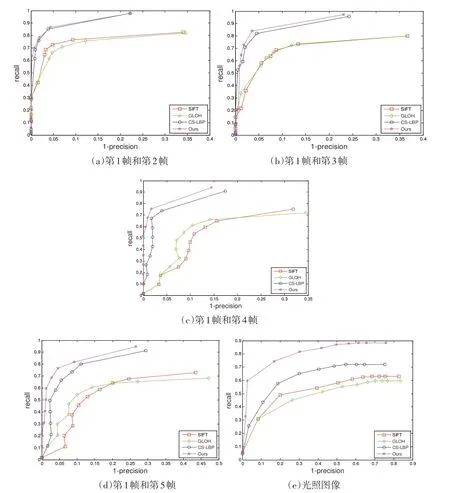
图5 特征描述性能比较Figure 5 Performance comparison on feature descriptions

其次，为了验证结合空间金字塔局部特征的谱匹配算法的精度，做了大量实验.图6和图7分别为尺度和旋转变换的序列图像，将本文提出的谱匹配算法与文献［5］中提出的N-SVD 谱匹配算法以及文献［7］中提出的Q-谱匹配算法进行比较.实验过程中参数值：R=2，N=6，T=0.01，L=3.在实验中，将序列图像中的第1帧作为参考图像，其余的图像为待匹配图像.

图6 Bip尺度变换序列图像（5帧）Figure 6 Image sequences of bip（scale transform）

图7 New York旋转变换序列图像（3帧）Figure 7 Image sequences of new york（rotate transform）

表1给出了Bip尺度变换序列图像在三种不同算法下匹配的实验对比结果.由表可知，本文算法能得到较高的匹配正确数和匹配正确率.N-SVD谱匹配算法以SIFT特征描述的相似性作为度量方式构造邻接矩阵，Q-谱算法以局部形状上下文相似性作为度量方式构造Laplace 矩阵，相比之下本文算法取得了更好的匹配结果，但随着变换越来越大，三种算法匹配精度都下降.

表1 Bip序列图像不同算法匹配结果Table1 Matching results of bip images in different algorithms

对于New York 旋转变换序列图像，三种算法对于第2、3、4 帧和第1 帧之间匹配的正确率都达到了92%以上，第5帧和第1帧匹配时，本文算法仍然保持了98%的较高正确率，N-SVD谱匹配算法以及Q-谱匹配算法正确率分别降到了85%和89%，图8给出了第5 帧和第1 帧匹配结果图，其中特征点总数为196，三种算法依次正确匹配点对数为193、166和175.由此可见，本文算法具有更好的旋转不变性.

图8 New York序列图像不同算法匹配结果Figure 8 Matching results of new york images in different algorithms

5 结语

针对基于谱分解的图像匹配算法中邻接矩阵度量方式问题，提出了一种基于空间金字塔局部特征描述，并将该特征描述之间的相似性作为度量重构邻接矩阵，利用谱分解的方法完成图像特征点的匹配.由于给出的局部特征描述在性能上优于传统的描述，因此,相应的匹配算法精度也得到了提高，特别是当图像发生较大光照、尺度和旋转变换时，相对于N-SVD和Q-谱算法，本文算法能取得更好的匹配结果.

［1］CONTE D，FOGGIA P，SANSONE C，et al.Thirty years of graph matching in pattern recognition［J］.Special Edition of the International Journal of Pattern Recognition and Artificial Intelligence on Graph Theory in Vision，2004，18（3）：265-298.

［2］SCOTT G L，LONGUET-HIGGINS H C.An Algorithm for associating the features of two images［J］.Proceedings of the Royal Society-Bio-logical Sciences，1991，B-244：21-26.

［3］SHAPIRO L S，BRADY J M.Feature-based correspondence：an eigenvector approach［J］.Image Vision Compute，1992，10（5）：283-288.

［4］PILU M.A direct method for stereo correspondence based on singular value decomposition［C］//Proceedings of IEEE Conference on Computer Vision and Pattern Reognition，1997：261-266.

［5］YUE S C，WANG Q，ZHAO R C.Robust wide baseline point matching based on scale invariant feature descriptor［J］.Chinese Journal of Aeronautics，2009，22（1）：70-74.

［6］TANG Jun，LIANG Dong，WANG Nian，et al.A laplacian spectral method for stereo correspondence［J］.Pattern Rec⁃ognition Letters，Elsevier，2007，28（12），1391-1399.

［7］梁栋，朱明，唐俊，等.基于局部相对形状上下文与Q-谱的点模式匹配算法［J］.电子学报，2012，40（4）：636-641.

［8］LOWE D G.Distinctive image features from scale-invariant keypoints［J］.International Journal of Computer Vision，2004，60（2）：91-110.

［9］MIKOLAJCZYK K，SCHMID C.A performance evaluation of local descriptors［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2005，27（10）：1615-1630.

［10］HEIKKILÄ M，PIETIKÄINEN M，SCHMIDB C.Description of interest regions with local binary patterns［J］.Pattern Recognition，2009，42（3）：425-436.

［11］OJALA T，PIETIKAINEN M，MAENPAA T.Multiresolution gray-scale and rotation invariant texture classification with local binary patterns［J］.Pattern Analysis and Machine Intelligence，IEEE Transactions on，2002，24（7）：971-987

［12］LIU Jingneng，ZENG Guihua.Description of interest regions with oriented local self-similarity［J］.Optics Commu⁃nications.2012，285：2549-2557.

［13］http：//www.robots.oxr.ac.uk/～vgg/research/affine/.

［14］FAN Bin，WU Fuchao，HU Zhanyi.Rotationally invariant descriptors using intensity order pooling ［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2012，34（10）：2031-2045.