动态介质中的光折射现象研究

张诗豪，刘 晓，史庆藩

(北京理工大学，北京 100081)

生活中我们常能在水盆、泳池及浅海底部看到不断变化，形态各异的光影图案，它们如此美妙，引人入胜，同时也使我们产生疑问:它们到底是怎么产生的?这些变化是否与不断波动的水面对光的折射有关?教科书中对于光的折射现象的介绍仅限于在静态介质中，很少提到在动态介质中的情况［1］。动态介质中光的折射问题因涉及入射光、水面形状、水深等多个因素而比较复杂，很难给出一个准确的定量描述，已有的文献或只是定性地解释这一现象的成因［2］，或只给出形式复杂的一般表达式［3］，致使这一问题仍存在很大的探讨空间。国际青年物理学家锦标赛(IYPT)更是在2012年将此问题设计成一个开放性问题，供全世界优秀学生进行研究和辩论。本文在此背景下进行研究并试图给出直观的定量描述。我们把一定区域内的水作为动态介质，对水面波浪和光线传播进行物理建模，再通过计算机编程模拟出不同水深处的光强分布图样，找出相邻两明(暗)纹中心间距、亮纹宽度和明纹平均亮度这3个物理量随水深的变化规律。

1 物理模型

以水作为动态介质，入射光为平行光并竖直向下射入水中，在照到水面波浪时会发生反射和折射，从而在水中形成一定光强分布。首先设立坐标系如图1所示。设x轴为波浪传播方向，y轴为竖直向下的水深方向，z轴为垂直于纸面向内的方向。同时假设水面波浪形状沿z轴方向一致，故只考虑xy面的二维情况。为简化起见，不考虑光在水中传播时的能量损耗以及光在水面波浪表面发生的反射现象，同时取波浪形状为理想正弦波y=sinx。考虑图1中x0处的入射光，根据折射定理:

式(1)-(4)中的θ为入射角，φ为折射角，n为水折射率，h0为波谷所对应的水深。联立求解可得出x0处入射光经水波折射后照射到对应深度h0的位置x1。按照几何光学原理，可以画出入射光经过折射后的光强分布，如图1所示。可以看出，不同水深处光强(明暗纹)分布的情况主要与深度h和水面波浪形状这两个因素有关。为了进一步深入探究明暗纹分布的变化规律，我们进行计算机模拟实验。

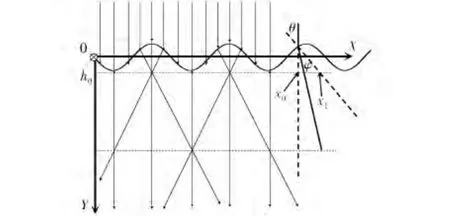
图1

2 计算机模拟

我们先研究某一时刻t时不同水深h处的光影图样，然后讨论某一深度h处不同时间t时的光影图案。水面范围取为0 m≤x≤100 m，入射光垂直入射，光强为I0。将水深h处沿x轴每隔0．01 m取一个点而均分成10 000个小区域，我们通过计算落到每一个小区域上的光强总合，得到不同x处每个小区域的光强I。

计算示例如图2所示，图中显示了深度h分别为3 m、5 m、21 m和34 m处的光强分布，黑线表示相应位置处水面波浪的形状，空心正三角形表示相应位置处I的大小，I值越大，对应区域越亮。

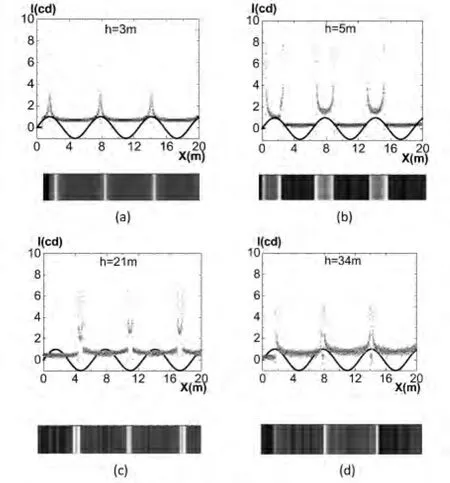
图2 同一时刻不同深度处的光强分布

从图2中可以看出各水深h处图样均呈现明暗周期性分布，即:当h=3 m时，最亮处为一个个尖锐高峰，如图2(a);随着h不断增大，最亮处由单峰“分裂”为2个半高峰，随着水深增加这2个半高峰的距离拉开，如图2(b)所示;随着h继续增大，2个半高峰又“汇聚”为单高峰，如图2(c)、2(d)所示;当h再增大时，则光强最大的尖峰会呈现“分裂”与“汇聚”的周期性变化规律。

3 分析与讨论

为了定量分析的目的，我们定义:最亮处为单峰形态时，单峰处为明纹，其它处为暗纹，如图2(a)、2(d)所示;最亮处为半高峰形态时，则相邻两峰间平均亮度大的区域为明条纹，小的为暗条纹，如图2(c)、2(b)所示。由于不同位置的光强分布不同，我们又引入Ia作为不同深度h处的平均亮度。

根据计算模拟，明纹宽度L和明纹平均亮度Ia随水深h的变化图像分别如图3和图4所示。另外，相邻两明(暗)纹中心间距为X=2π，与h无关。

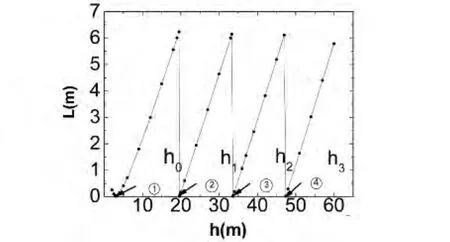
图3 明纹宽度随水深的变化图

图4 明纹平均亮度随水深的变化图

由图3和图4可见，当h≤h0时，随着深度h的不断增加，明条纹宽度L逐渐变窄并趋于0(见图3)，明纹平均亮度Ia则不断增加直至第一个亮度高峰(见图4);当h0＜h＜h1(①区)时，L随h的增大而线性增加(见图3)，Ia随h的增大而不断减小(见图4);当h=h1=19．65时，L的数值由接近于2突变为无限趋近于0(见图3)，Ia由小于1突变至第2个亮度高峰(见图4);当h1＜h＜h2(②区)时，L随h线性增加(见图3)，Ia不断减小(见图4);当h=h2=33．6时，L再次由接近2突变为无限趋近0(见图3)，Ia由小于1突变至第3个亮度高峰(见图4);当h2＜h≤h3(③区)时，L和Ia的变化规律与①区和②区情况相同，整体呈现规律性变化。

另外，当水波以波速v沿x轴方向运动时，即y=sin(x+vt)，则各水深h处的明暗图样随水波以速度v整体沿x轴移动。此时，根据我们的模拟结果可以通过探测水中的光强信号来测出水波速度v，即:根据探测器所处水中深度h的不同，可以检测到光强峰值的间隔Δt为一定值，对应水波速度 v=X/Δt，X=2π;也可以检测到峰值间隔为Δt1和 Δt2，则对应水波速度 v=2π/(Δt1+ Δt2)。由此，我们得到了一种测量水波速度的方法。

4 小 结

本文通过探究水中光影图案的成因研究了动态介质中的光折射问题，给出了介质深度不同时光强分布的模拟图样，发现了明(暗)纹中心间距、明纹宽度和明纹平均亮度等物理量随介质深度变化的规律，同时提出了一种测量水波速度的方法。本文只考虑了有限区域内的动态介质，无限区域内的动态介质的相关研究有待于进一步的讨论。本文结果不仅对大学物理光学类课程教学具有一定的意义，而且对实际应用也具有一定的参考价值。

［1］ 赵凯华、钟锡华．光学［M］．北京:北京大学出版社，2008．35-55．

［2］ Jearl Walker．Shadows cast on the bottom of a pool are not like other shadows［J］．Amateur Scientist，July 1988，Am．259，116-119．

［3］ Jenet Shields．Swimming pool optics［J］．Optics and Photonics News，1990，1(9):37．