基于超声波的食盐溶液物性的研究

尹少英，刘 轩，徐在春，张玉军，韩 旭

(哈尔滨学院，黑龙江哈尔滨 150086)

密度是表征物体物理特性的物理量，在日常生活和工业生产中是很重要的基本参数之一。目前，在实验教学中测量液体密度方法主要是根据密度基本公式的直接测量，例如:液体静力称量法［1］、比重瓶法、焦利秤法［2］等，这些方法原理简单但操作烦琐，测量准确度受到仪器精确度限制;还有一种间接测量方法是利用振动方法测量液体密度［3］，但其实验原理涉及结构力学和机械振动等知识，实验原理相对复杂。液体的体积模量是描述液体性质的重要物理量，是表征液体材料力学特性的重要参数，在各种工程机械的液压与减振系统中，对液体的体积模量的大小和准确性要求很严格。目前，在实验教学中没有用来测量该物理量的教学设备。由于超声波具有方向性好、穿透能力强、易于产生和接收、探头体积小等特点。因此，我们在实验教学中设计了利用超声波测量液体密度和体积模量的实验题目。

本文利用声速测定实验仪、示波器和液槽等实验设备测量了水的密度，实验现象直观，原理和操作过程相对简单，使得测量精度也有很大提高。配制了45种不同浓度的食盐溶液，根据实验数据对食盐溶液的相关物性进行了详细研究。

1 实验原理与方法

测量超声波在液体中的传播速度有两种方法:相位法和共振法［4］。该实验使用相位法来测量超声波传播速度。相位法的实验原理是:在传播方向上找到任意两点，这两点的振动状态相位相同或者是2π的整数倍时，在这时我们测得的这两点之间的距离就设为L，即L=nλ(n为一正整数)。发射端换能器将电信号变为近似于平面波的声波信号，接收端换能器垂直于波的传播方向放置，其端面上各点都具有相同的相位。沿传播方向移动接收器时，总可以找到一个位置使得接收的信号与发射器激励信号同相。继续移动接收器，直到接收的信号再一次和发射器的激励电信号同相时，移过的这段距离必然等于声波的波长。移动过程中，示波器会出现李萨茹图形，选择右斜或者左斜的直线(即同相或反相)作为参考标准，从而准确的记录下此时的位置，使得测量的波长更准确。超声波的频率已知，可利用v=fλ求得超声波传播速度。根据溶液的浓度求出密度，然后根据液体的体积模量和密度关系求出液体的体积模量。其关系式为［5］:

其中:v是超声波在液体中传播速度，K为液体的弹性模量，ρ为液体的密度。

2 测量结果与讨论

在室温t=18．6℃下，利用QSSV-2型声速测定实验仪、示波器和一个液槽来测定超声波在水中的传播速度。将信号发生器的频率调为40 KHz。已知超声速的传播速度v、声波频率f和波长λ的关系为v=fλ。本实验采用相位法测得数据和逐差法计算的波长见表1。

表1 位置和波长记录表

由超声波波速计算公式

已知水在常温下体积模量

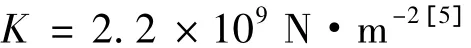
由公式(1)得水密度的测量值

已知水密度的标准值 ρ0=1 000 kg·m－3，则水密度的测量值与标准值的百分误差

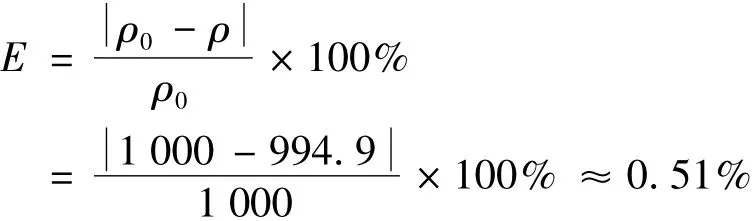
利用超声波测量水密度的百分误差小于1%，由此可见利用超声波法测量液体密度的准确度较高。与传统方法(液体静力称量法、比重瓶法、焦利秤法)相比，该实验方法具有操作过程简单、实验原理通俗易懂，由于超声波具有方向性好、穿透能力强、易于产生和接收、换能器体积小等特点，使得测量精度较高。因此使用该种方法测量液体密度在实验教学和应用［6-7］中具有一定优势。

在室温t=18．6℃ 下，以步长为0．5% 配制了浓度从0．0% 增到22．0% 的45种不同浓度的食盐溶液。对不同浓度的食盐溶液，利用相位法和逐差法计算出超声波在溶液中的传播速度;由于实验时液槽中水的体积为6L，才能将换能器完全浸没在水中，加入一定的食盐后，体积几乎变化不大，因此假设溶液体积不变前提下，计算出不同浓度食盐溶液的密度;然后利用公式(1)，通过超声波在溶液中的传播速度与溶液密度计算出溶液对应的体积模量。由于计算过程繁琐，这里只给出测量结果见表2。

表2 不同浓度食盐溶液的密度、超声波速度和体积模量

根据表2中数据，利用绘图软件得到在不同浓度食盐溶液中超声波传播速度与浓度的关系图，如图1(a)图所示:由a图可以看出食盐浓度与声速呈线性关系的，利用最小二次拟合得到定标公式标公式为

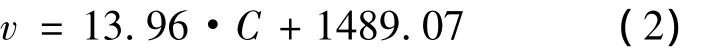
式中:v代表超声波在液体中传播速度，C代表食盐溶液浓度。图1(a)图中用红色直线画出了拟合线，图中绿色长划线是来自文献李志坤［8］等文章，而黑色短划线来自杨燕婷［9］等文章，它们都表现很好的线性关系。在浓度较大时，传播速度表现出偏离，其可能原因有两个:一是测量误差所引起的，李志坤等文章拟合的数据点有5个;二是测量条件不同，例如使用超声波频率、环境温度等不同，详细情况请见相关文章。

将表2中食盐溶液密度与超声波传播速度的对应关系利用绘图软件画出，在图1(b)图可见两者存在很好的线性关系，利用最小二乘法给出了溶液密度与声速的定标公式为

式中:D代表食盐溶液的密度，v表示超声波在其中传播速度。查阅文献可知随密度增加，传播速度也会增加，该实验结果表明它们之间存在线性关系。

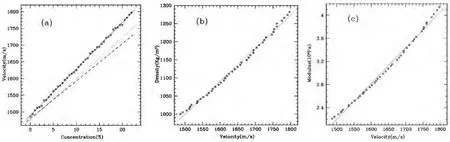
图1 溶液浓度、密度、体积模量与超声波传播速度关系图

利用相位法很容易得到超声波在溶液中传播速度，而溶液的体积模量是一个重要的物理参数，因此也研究了溶液体积模量和声速之间的关系。在图1中(c)图可以看出两者之间存在很好的线性关系，拟合出准

确的定标公式

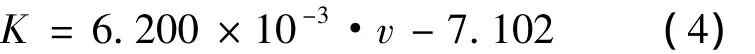
式中:K代表食盐溶液的体积模量，单位为109Pa;v表示超声波在其中传播速度，单位为m·s－1。只要能够测得超声波在食盐溶液中的传播速度，可以根据公式(4)得到它的体积模量。曾育锋［10］等人研究了不同浓度食盐溶液的体积模量，发现溶液浓度与体积模量之间存在线性关系，此结论可由公式(2)与(4)得出。

通过以上实验结果分析得:在温度保持不变时，超声波的传播速度、液体的体积模量随着溶液浓度的增加而增加。其理论解释为:纯水中水分子之间的距离较大，而随着食盐溶液浓度的增加，原有水分子空隙被食盐分子部分填充使得分子的平均间距减少，因此液体的弹性模量(加在单位面积液柱上的压力与引起液柱长度相对变化量的比值)变大，而且液体体积模量的变化比例大于浓度增加时导致的密度的变化比例，从而导致声速v变大。本实验结果很好的证明了理论的正确性，并表明超声波的传播速度与液体的体积模量、浓度(密度)之间存在很好的线性关系。

在本实验中影响实验误差来源主要是:一是实验时室温很难控制在恒温状态，劳振花等人［11］和岑敏锐［12］研究表明温度对液体的弹性模量和声速有一定的影响。二是计算不同浓度溶液密度时忽略了溶液体积的微小变化。最后本实验使用超声波频率40 KHz，波束能量较小，在浓度较大的溶液中测量声波波长时，声波信号衰减较大，给测量结果带来一定误差［13-14］。

3 结 论

根据超声波法得到水密度的测量值，其相对误差为0．51%。该实验原理简单，操作方便，精确度较高等优点，可以设置为本科实验教学中的实验题目。

利用超声波对配制的45种食盐溶液的物性进行仔细研究，根据实验数据，分别拟合出超声波的传播速度与溶液的浓度、密度以及体积模量之间定标公式，得出它们之间都存在较好的线性关系。实验结果与文献资料和理论推测相吻合，该实验采集数据点较多，实验结论具有一定说服力。

利用该实验装置可以测量超声波在空气中传播速度和在不同液体中传播速度，可以测量液体的密度和体积模量，稍加改动可以实现测微距等实验。实现一套仪器设备开发多个实验题目，减少了实验教学设备经费，又能开设了多个实验项目。可以作为大学高年级的综合与设计性实验题目，通过该实验项目，既能开拓了学生视野又能锻炼了动手能力，提高学生综合设计实验的能力和实验创新能力。同时让学生学习到了超声波的理论知识和了解到其实际应用，起到理论知识和实践相结合的作用。

［1］ 顾英姿，陈朝晖，许常红，等．液体静力称量法液体密度测量及其不确定度评定［J］．计量技术，2006(6):8-11．

［2］ 王好仁，胡毅．液体密度的测量及比较［J］．北京电力高等专科学校学报，2012(7):382-384．

［3］ 陈 明，严勇，张秋华，等．用振动方法测量流体密度［J］．力学与实践，2004，26(1):62-63．

［4］ 浙江求是科教设备有限公司．QSSV-2超声波声速测定仪产品说明书．2006(5):62-68．

［5］ 张凤兰．超声场观测法测液体的体变模量［J］．延边大学学报:自然科学版，2003，29(2):151-153．

［6］ 蔡朝鹏，于瀛蛟，张蕊，等．用声波方法测量液体密度的实验研究［J］．石油仪器，2008，22(6):7-9．

［7］ 姚明林，陈先中，张争，等．超声波液体密度传感器［J］．传感器技术，2005，24(5):57-60．

［8］ 李志坤，高本领，张俊．液体表面张力系数、声波在液体中传播速度与液体浓度关系的研究［J］．大学物理实验，2010，23(6):56-59．

［9］ 杨燕婷，王敏，周莹，等．超声光栅测量溶液中超声声速与浓度关系研究［J］．实验技术与管理，2011，28(7):32-35．

［10］曾育锋，涂辉．超声光栅测量液体体积弹性模量实验研究［J］．实验技术与管理，2012，29(4):53-54．

［11］劳振花，姜兆波．液体体积弹性模量与温度关系测量实验研究［J］．科学技术与工程，2009，9(2):386-390．

［12］岑敏锐．超声波在液体中的传播速度与温度的关系［J］．物理实验，2008，28(5):39-41．

［13］李志杰，赵骞．超声波声速测量方法的探讨［J］．大学物理实验，2012(4):26-28．

［14］李艳琴．不同介质中超声波传播速度测量方法之比较［J］．大学物理实验，2014(2):30-34．