全铌超导Josephson结的EWB仿真模型
宿非凡,王瑞峰
(1.中国科学院物理研究所,北京 100190;北京交通大学,北京 100044)
自从约瑟夫森(Josephson)于1962年发现了Josephson效应以来,超导电子学取得了迅速的发展。作为超导电子学的最基本原件——Josephson隧道结,无论是对其的理论研究还是其制备工艺的研究改进都是十分有意义的[1-4]。
近几年来国外已经有一些软件可以用来对Josephson结进行直接的模拟仿真,比如 Wins、JSpice等,然而这些软件的各种功能还不能让人满意,现阶段还无法满足Josephson结研究的具体要求。
EWB是目前的一种最简单、最普遍的分析和模拟各种电路的有力工具,而且可以采用图形输入方式,操作界面直观[5]。其分析功能强大,利用它可以方便的求出电路各种变量的时域、频域等特性。
如果能够利用这个软件对约瑟夫森结进行仿真研究,可以大大提高工作效率、降低劳动量。同时,可以将约瑟夫森结与外电路很好的结合在一起,所以该模型将具有物理意义突出,物理图景明显的特点。
1 Josephson效应简介
约瑟夫森效应也就是我们所说的非线性量子隧道效应,两块超导体中间加一层很薄的绝缘层,即构成一种典型的Josephson结。在这种情况下,绝缘层相当于一个势垒其势能高于Cooper Pair的动能。根据经典理论,我们知道Cooper Pair是不可能穿过这个势垒的。但是,根据量子理论Cooper Pair有一定的概率可以穿过这个势垒,这种量子的隧道效应就是约瑟夫森效应产生的物理基础。
根据微观的BCS理论,超导体在进入超导态后,超导电子结合成库珀对。这些库珀对彼此交叠渗透导致整个超导体中的超导电子有相同的有序度。当两块超导体相距很远时,它们序参量的位相必然不相关;当它们合并在一起时,位相必然相同;如果它们处于既不远离、也不合并,那么它们之间必然存在某种关联,使它们的位相既非完全相同也非毫不相关,而是维持一定的关系。
1965年Josephson将约瑟夫森结满足的电动力学规律总结为Josephson方程组的四个方程:
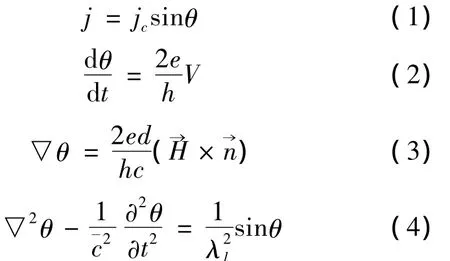
其中:θ为绝缘层两侧的电子波函数的相位差,j为流过约瑟夫森结的电流密度,jc为这个约瑟夫森结的临界电流密度,V为结两侧的直流电压值,→H为磁场强度。d为外磁场在势垒区附近的有效穿透深度,其值为d= λ1+ λ2+t,λ1、λ2为绝缘层两侧超导体的穿透深度,t为绝缘层的厚度,¯c为电磁波在约瑟夫森结中的传播速度。
2 Josephson结的I-V特性曲线和常用模型
2.1 Josephson结的I-V特性曲线
由于约瑟夫森结中绝缘层的存在,所以结的超导层之间会出现电容特性。这个电容特性会引起约瑟夫森结的I-V回滞。约瑟夫森结典型的I-V特性,见图1。
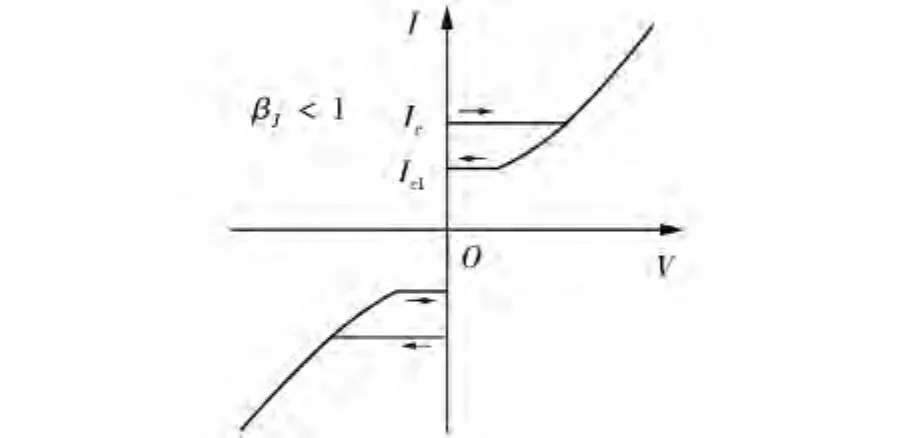
图1 约瑟夫森结典型的I-V特性曲线
图1 中显示出来的非线性特性在实际的许多应用之中是不利的,根据电路的相关知识我们知道,可以在约瑟夫森结上并联一个定值电阻来减小这种回滞现象。这时候Josephson结的I-V特性,见图2。
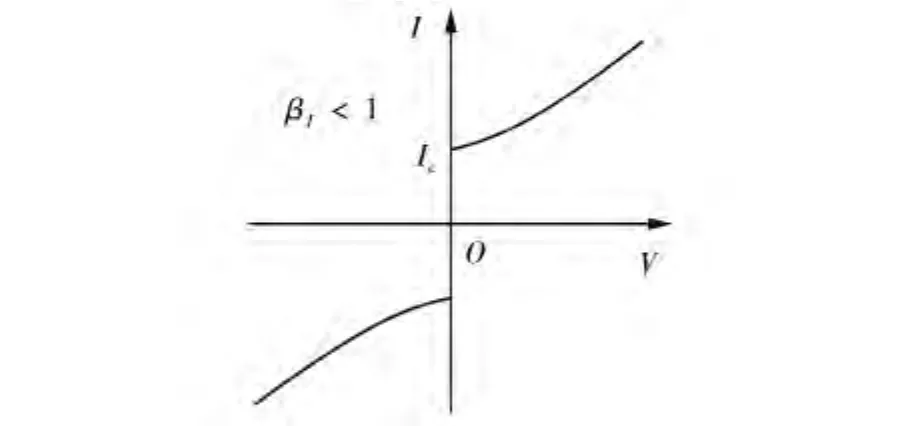
图2 消除回滞后约瑟夫森结典型的I-V特性曲线
在这种特性曲线中,随着电压的增大和减小,特性曲线是可逆的。当I>IC时电压由零电压状态跳变至有限电压状态。在有限电压状态,特性曲线遵从欧姆定律,表现出有限电阻的特性。
2.2 Josephson结常用模型
对于实际的Josephson结,可以将其视为一个满足I=ICsinθ的理想Josephson结与耗散电阻R,结间分布电容C并联的模型,其等效电路见图3,这就是常用的Stewart-Mc Cumber模型,也常称为RCSJ(电阻一电容并联Josephson结)模型。
在这个电路中,外加电流源时,总电流可以表达为:
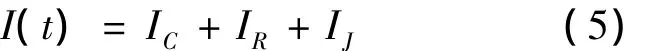
其中:IC、IR、IJ分别表示流过电容器,电阻和理想Josephson结的电流。将其展开有:
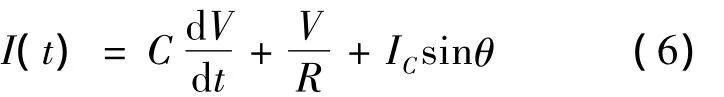
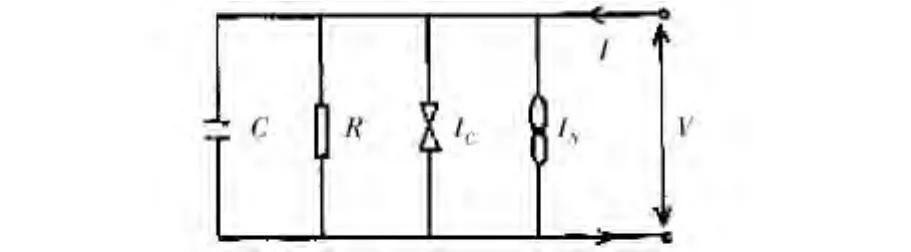
图3 Josephson结的RCSJ模型等效电路图
有这样一种情况,当Josephson结的耗散电阻R很小以至于分布电容C相当于开路时,RCSJ模型简化为一个理想Josephson结与电阻的并联,即所谓的RSJ模型。其等效电路图见图4。
这种情况下有βC>>1,所以相应的电流表达式应该改写为:
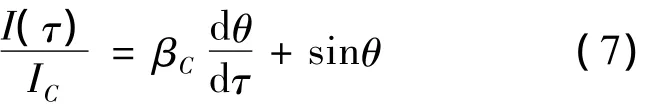
另外一些Josephson结模型比较复杂,超出了本文的研究范围这里不再赘述。
3 Josephson结的电路(EWB)模型与仿真
3.1 电路仿真软件EWB
目前对 Josephson结的仿真研究,由于Josephson结的高度非线性特点,基本上都要采用数值计算的方法。但是应用这种方法需要建立复杂的微分方程(组)并求解,这样无疑会带来效率较低、劳动繁重的问题。最近也有课题组采用Matlab建立模型进行仿真研究,但是这种方法仅相当于采用建立模型的方法来求解微分方程,仅降低了求解微分方程的工作量,物理意义不够突出,物理图像不够明显。
EWB是目前的一种最简单、最普遍的分析和模拟各种电路的有力工具,可以大大提高工作效率、降低劳动量。同时,其将约瑟夫森结与外电路很好的结合在一起,所以该模型将具有物理意义突出,物理图景明显的特点。
本文首次提出了基于EWB简单电路的理想Josephson结模型,并利用这个模型对Josephson结的特性进行了详尽的仿真研究,仿真结果与实验测量的实际结果相比较可以表明该模型是正确合理的。
3.2 Josephson结的电路(EWB)模型
为了在EWB中得到理想Josephson结的电路模型,我们先将(2)式对时间t积分一次并将积分的结果代入(1)式,可以得到:
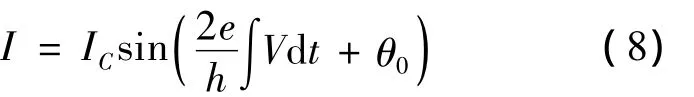
为了全面的仿真研究Josephson结及其重要应用SQUID,我们保留(8)式中的初相位θ0,这样一来我们根据(8)式就得到了EWB中得到理想Josephson结的电路模型,其电路见图5。
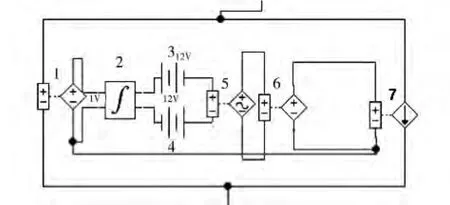
图5 理想Josephson结的电路模型图
图5 中的所有元件均由EWB的标准元件库提供,其中各元件分及其作用如下:
(1)电压控制电压源,其作用是将Josephson结两端的电压送给下一部分的电学元件,其放大系数为1;
(2)理想积分器,其作用是对电压控制电压源输送来的电压进行积分,其积分系数为3.038 5 × 1015
(3)、(4)直流电源,其作用是将(8)式中的初始相位表现在电路中;
(5)电压控制正弦函数发生器,其作用是将上一级输送来电压的正弦函数输出;
(6)放大器,其作用是将Josephson结的临界电流值 IC表现在电路中,其放大系数就是Josephson结的临界电流值IC;
(7)电压控制电流源,其作用是将上一级输送来的电压值等效转化为电流值,以便将我们的模型接入外部电路中,其系数为1。
不难看出,我们的模型完全是根据由约瑟夫森方程组推导而来的(8)式得到的,其物理意义十分明显,物理图景清楚。
这样一来,我们就在EWB中得到了理想的Josephson结的全电路模型。电路按上图连接好以后可以进行集成,集成好的理想Josephson结表示为图6的形式,下面的仿真过程中我们均以此符号表示理想的约瑟夫森结。

图6 集成理想Josephson结电路符号
以上获得的是理想Josephson结的模型。对于实际Josephson结RSJ模型,我们只要在模型上并联一个电阻即可,对于RCSJ模型,在RSJ模型原基础上再并联一个电容即可。
3.3 理想Josephson结在EWB中的模型的验证结果
我们利用图7形式的电路来进行仿真。可以看到图中电阻R与理想的约瑟夫森结J并联构成了实际Josephson结的RSJ模型。我们将并联电阻设定为0.5 Ω,Josephson结的临界电流设定为0.4A,理想电流源提供1A的直流恒定电流。
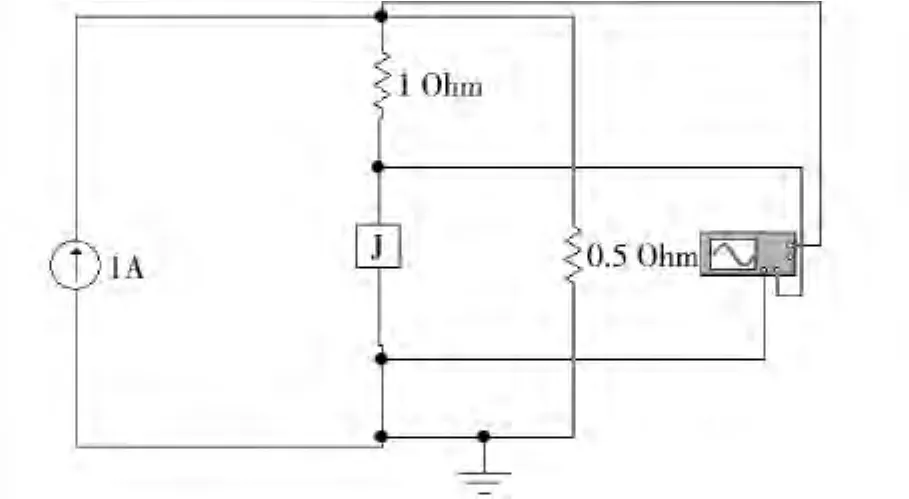
图7 仿真用的Josephson结RSJ模型电路图
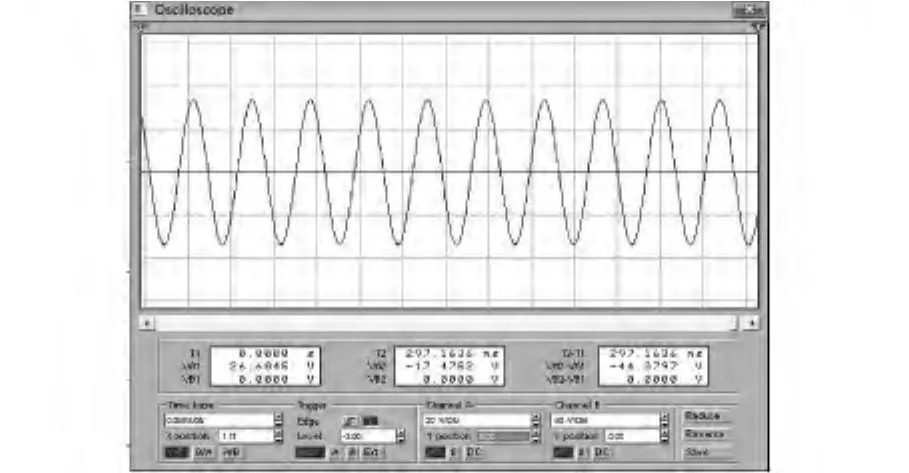
图8 恒定电流源驱动获得的结两端电压波形
图8 为恒定电流源驱动获得的结两端电压波形,可以看出当给Josephson结通过恒定电流(大于其临界电流)的时候,Josephson结两端的电压是周期震荡的,可以看出波形中存在高次谐波成分。
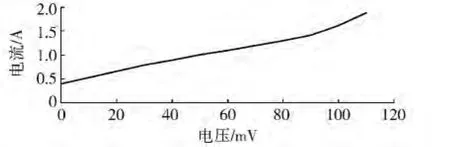
图9 Josephson结RSJ模型I-V特性曲线
由仿真结果我们发现,理想Josephson结的电压随时间的变化曲线不是严格的正弦曲线,而是经过调制的曲线。出现该现象的原因是由于理想Josephson结存在混沌现象。从仿真得到的I-V特性可以明显看出,当流过Josephson结的电流小于其临界电流时,Josephson结两端的电压为0,而当电流超过临界电流时,Josephson结两端出现电压。这与直流约瑟夫森效应一致。
对RSJ模型的I-V特性进行仿真时,我们使用电路如图7,理想Josephson结(IC=0.4 A)和R构成实际Josephson结的RSJ模型;采用EWB自带的示波器,重复仿真过程就可以得到不同偏置电流下Josephson结的I-V特性曲线。
图10是我们仿真获得的RSJ模型在具有不同并联电阻R值时的I-V曲线,图中曲线所对应的并联电阻 R 值分别为 0.50 Ω、0.75 Ω 和 1.00 Ω(图中从上到下依次为 0.50 Ω、0.75 Ω、1.00 Ω临界电流分别对应 0.4 A、0.6 A、0.8 A)。
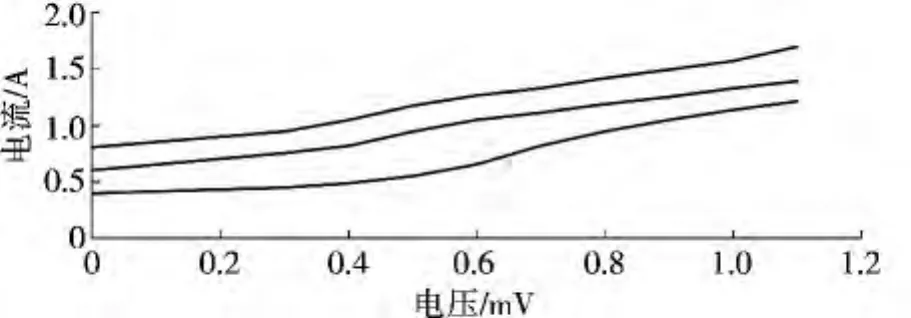
图10 不同电阻下Josephson结的RSJ模型I-V特性曲线
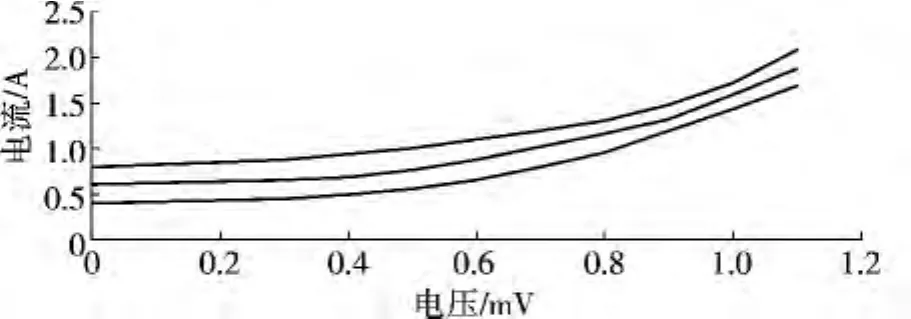
图11 标准理论曲线
为了方便对比,图10为标准理论所得到的曲线[5],将图9与之相比较可以看出我们仿真得到的I-V特性曲线理论标准方法得到的结果相一致,这无疑说明我们提出模型和仿真方法是正确可行的。
对RCSJ模型I-V特性进行仿真时,我们使用图12所示的电路,图12中理想约瑟夫森结(IC=0.1 mA)、电阻 R=3.2 Ω、电容 C 并联构成实际Josephson结的RCSJ模型。仿真时采用同样分析方法,得到了RCSJ模型的I-V特性,如图13(a)~(c)所示。三图均可以看出明显的回滞,这是与标准理论相符的。
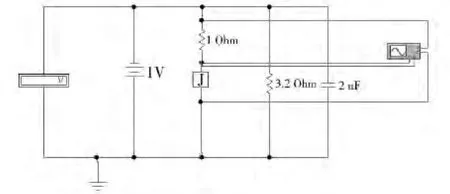
图12 对RCSJ模型仿真电路图
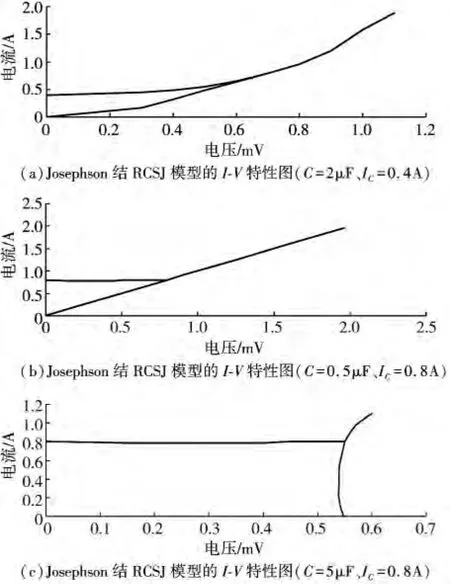
图13 Josephson结的特性曲线
仿真结果与第三章第二节描述的回滞I-V曲线一致,也与参考文献给出的结果一致,后面章节中将其与实验实际测量(C=5μF、IC=0.8 A)的结果进行了比较也得到了很好的匹配度。这再次说明了该模型可以确实地用于表示Josephson结[7-12]。
4 Josephson结特性的实验测量
为了完整的研究约瑟夫森结的物理特性,验证模型的可靠性。进行了实验测量验证。
从恒流源输出的电流经过低频滤波后输入到Josephson结。本实验中滤波器的截止频率为100 Hz,测量过程中用铅筒作为样品的超导屏蔽,在液氦(4.2 K)中进行测量。
图14为测量得到的Josephson结的I-V特性曲线。样品为SNAP工艺制作。
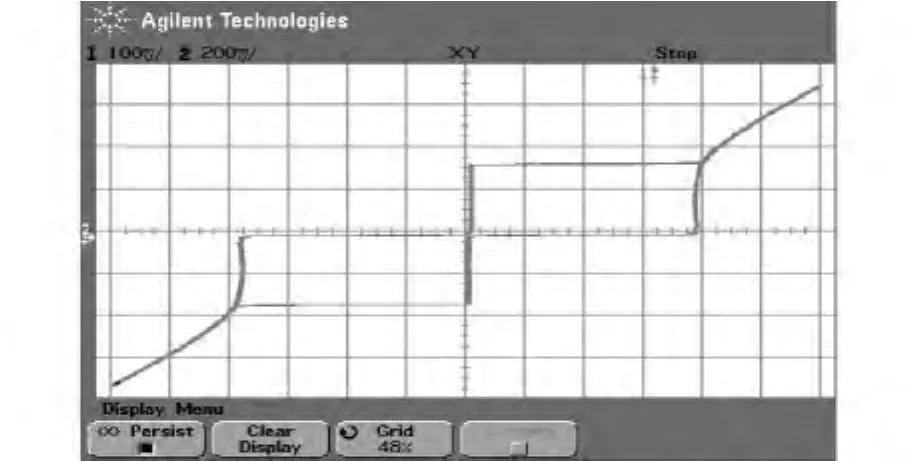
图14 实验测得的JosephsonI-V特性曲线

图15 实验用测量环境液氦恒温器图
如图14与图15所示,可以看出EWB电路模型模拟的Josephson结I-V特性曲线与实验实际测量得到的Josephson结I-V符合的很好。所以我们有充足的理由相信,本文提出的Josephson结EWB电路模型既可以与标准理论的结果相符合又可以与实验结果相符,所以模型是完全有效的。其可以方便的求出电路中各种变量的动态特性,操作简单,功能强,利用这个软件对Josephson结进行仿真研究,可以大大提高工作效率。
6 结 语
为了方便对约瑟夫森结的特性进行仿真计算,在EWB软件中定义了Josephson结模型,这样就可以利用EWB强大的运算功能方便快捷地进行Josephson结电路的模拟和仿真。使用模型仿真了Josephson结最主要的I-V特性,仿真结果与实际相符,这说明我们定义的模型是有效可用的。实验制备了全铌的Josephson结,选出了比较理想的样品进行实验。
在测量时复杂的实验环境中的电磁环境使得精确的测量变的十分困难,可能出现在不同的时间段进行同一实验得到不同的结果;此外,在使用EWB进行仿真时,对于同样的电路,不同的仿真参数设置可能导致仿真结果的本质变化,如何设置正确的仿真程序仍需要进一步的研究。
[1] 赵忠贤,陈立泉,等.Ba-Y-Cu氧化物液氮温区的超导电性[J].科学通报,1987,32:41.
[2] 张裕恒.超导物理[M].3版.合肥,中国科学技术大学出版社,2006.
[3] 章立源,等.超导物理[M].3版.北京,电子工业出版社,1997.
[4] 林德华.超导物理基础与应用[M].重庆,重庆大学出版社,1992.
[5] 江米双,丁玮蓉,等.Excel环境下正弦信号源RLC串联电路模拟[J].大学物理实验,2012(2):59-62.
[6] 黄昆,韩汝琦.固体物理学[M].北京,高等教育出版社,2009.
[7] 张军琴,杨银堂,贺庆丽,等.超导Josephson结直流I-V特性的数值计算.计算物理[J].2006,2 3(1):98-102.
[8] 漆汉宏,田永君,王天生,等.高温超导双晶结 dc SQUID的I-V特性仿真研究系统仿真学报[J].2004,16(7):1421-1424.
[9] 曾谨言.量子力学卷Ⅰ[M].北京:科学出版社,2000:112.
[10] Josephson B D.Phys Rev Lett[J].1(7)(1962),251.
[11] Josephson B D.Rev Mod Phys[J].36(1964),216.
[12] Josephson B D.Adv Phys[J].14(1965),419.

