非元反应速率方程初探*

余高奇 谭联侨 陈阳 何选明 屈小英 周华

(武汉科技大学化学工程与技术学院 湖北武汉430081)

非元反应速率方程初探*

余高奇 谭联侨 陈阳 何选明 屈小英 周华

(武汉科技大学化学工程与技术学院 湖北武汉430081)

将化学动力学与数学分析相结合,探讨了非元反应经验速率方程和速率方程的积分形式;以H2+ Br2=2HBr及一些单分子气相反应为目标反应,讨论了浓度、压强对反应速率常数的影响。研究表明:对于非元化学计量反应a A(aq)+b B(g)+……+y Y(aq)+z Z(g),经验速率方程为:;速率常数k的单位为mol·m-3·s-1,与反应级数无关;浓度、压强对非元反应速率常数影响显著。

非元反应 速率常数 单分子气相反应 反应级数

化学反应速率方程是化学动力学研究的重要内容,化学反应速率方程的建立对全面认识某化学过程具有极其重要的意义[1]。本文将数学分析与化学动力学相结合,提出了化学反应经验速率方程,推导了不同反应级数速率方程的积分形式;并就浓度、压强对H2+Br2=2HBr[2]及一些单分子气相反应[3]的影响进行了初步探讨,试图从另一个角度诠释非元反应速率方程的基本特点。

1 非元反应经验速率方程

对于非元化学计量反应:

由实验数据得出的经验速率方程可表示为:

式(2)中cθ=1.0mol·m-3,pθ=100×103Pa;ci(i=A、Y…)、pj(j=B、Z…)依次为溶液相i组分物质、气相j组分物质的浓度和分压,单位分别取mol·m-3和Pa,下同;nA、nB…nY、nZ分别称为反应组分A、B…Y、Z的表观分级数,总的表观反应级数n=nA+nB+…+nY+nZ;k称表观速率常数,其单位与v相同,即为mol·m-3·s-1,与反应级数无关。

式(2)亦可简写为[4]:

同理,如果化学计量反应(1)为元反应,则其速率方程可表示为:

即元反应的反应速率与反应物浓度(压强)数值的相应方次成正比,其方次即为元反应中各反应物的系数。

式(4)中的a和b分别称为反应物A和B的分级数,元反应的总级数n=a+b;k称速率常数,单位为mol·m-3·s-1,与反应级数无关。

传统的速率理论认为反应速率常数单位是由反应级数决定的,对于一些复杂反应量纲的讨论非常繁琐,同时也缺少合理性与必要性[5-9]。

2 速率方程的积分形式

速率方程的积分形式(即反应物浓度与时间的函数关系式)对于得出指定时间内某反应组分的浓度,或达到一定转化率需要的时间具有不可替代的作用。

对于反应:A→产物,不同反应级数相应的速率方程积分形式推导如下。

2.1 零级反应

若反应速率与反应物A浓度的零次方成正比(即零级反应),存在:

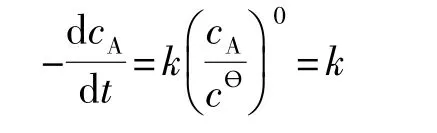
则:

式(5)中cA,0表示反应物A的初始浓度,cA为某时刻A物质的浓度,t为时间(单位为s),下同。

2.2 一级反应

若反应速率与反应物A浓度的一次方成正比(即一级反应),存在:

有必要指出,自然对数函数是典型的超越函数,要求其后参数无量纲,式(6)可满足要求。

2.3 二级反应

若反应速率与反应物A浓度的二次方成正比(即二级反应),存在:

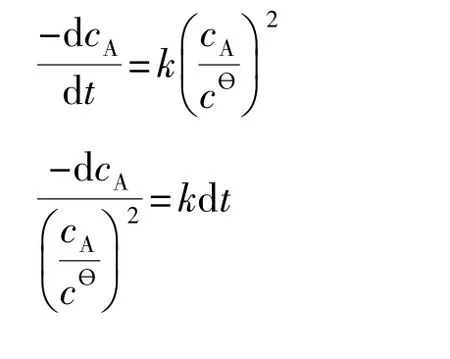
2.4 n级反应

若反应速率与反应物A浓度的n次方成正比(即n级反应),存在:

由上述结果可得反应速率常数k的单位为mol·m-3·s-1。

3 浓度、压强对非元反应速率常数的影响

3.1 浓度的影响

1906年,Bodenstein通过测定得出反应H2+Br?HBr的速率方程为[10-11]:

令:

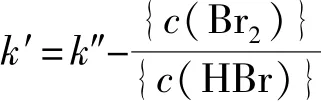
代入式(9),可得:

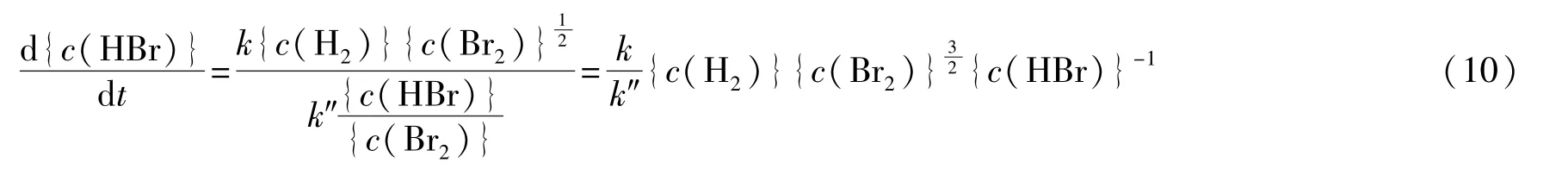
因此反应H2+Br22HBr的表观速率常数(比速率)为,H2的表观反应级数为1;Br2和HBr传统意义上的表观反应级数需由实验归纳[12-13]。

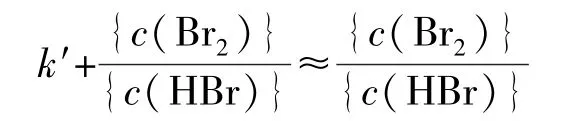
对应的速率方程式转化为:

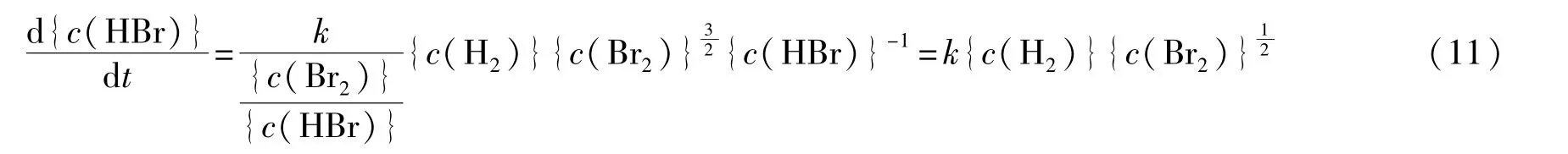
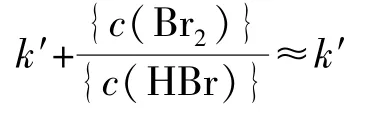
对应的速率方程变为:

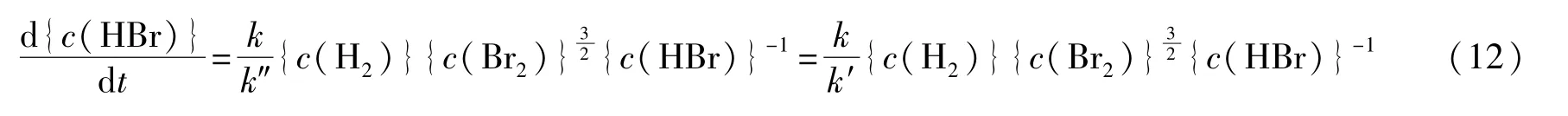
由此可知非元反应速率方程式中的反应级数及速率常数均与组分浓度有关。

3.2 压强的影响

实验表明,一些单分子气相反应

在高压下为一级反应,在低压下为二级反应;对应的速率方程为[3]:

令:

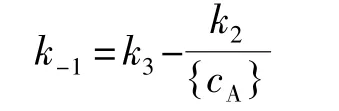
代入式(13)得:

此时该反应的表观级数为2,表观速率常数为k1。

由此可知压强既可影响非元反应的反应级数,又可影响非元反应的反应速率常数。

4 结论

对于非元化学计量反应

有如下结论:

①经验速率方程可表示为:

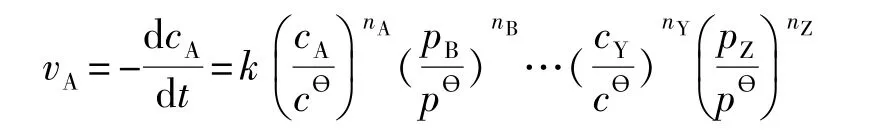
②速率常数k的单位为mol·m-3·s-1,与反应级数无关。

③浓度、压强对非元反应的表观速率常数和表观反应级数均有影响。

[1] Peter H,Peter T,Michal B.Rev Mod Phys,1990,62(2):251

[2] Boudart M.Catal Lett,2000,65:1

[3] Richardson W,Volk L,Lau K H,et al.Proc Nat Acad Sci USA,1973,70(5):1588

[4] 天津大学物理化学教研室.物理化学.第5版.北京:高等教育出版社,2009

[5] Bokhoven C,Gorgels M J,Mars P.Trans Faraday Soc,1959,55:315

[6] Isaacson A D,Truhlar D G.JChem Phys,1982,76(3):1380

[7] Guggenheim E A.JChem Educ,1956,33(11):544

[8] Cai Z T,Wang ZG,Deng C H.Chin Sci Bull,1993,38(19):894

[9] 朱长缨.华中师范大学学报(自然科学版),1985(3):125

[10] Arthur L.JPhys Chem,1958,62(5):570

[11] Bauer SH.Science,1963,141:867

[12] 史焱,詹先成,吕太平,等.化学学报,2006,64(6):496

[13] Liu H,Tan J,Yu H X,et al.Int JEnviron Res,2010,4(3):507

*湖北省教育厅教改项目(No.2008191);武汉科技大学校改项目(No.2007050X)