铸造凝固过程宏观偏析数值模拟研究

涂武涛 沈厚发 柳百成

(清华大学材料加工系，北京100084)

试验研究

铸造凝固过程宏观偏析数值模拟研究

涂武涛 沈厚发 柳百成

(清华大学材料加工系，北京100084)

宏观偏析普遍存在于铸造合金凝固过程中，严重影响了材料的使用性能。本文利用宏观偏析数学模型，分别对53 t钢锭和500 t铸件宏观偏析进行数值模拟研究。模型考虑了凝固收缩与等轴晶沉降，模拟结果和实验结果吻合较好。

铸造凝固过程;宏观偏析;数值模拟

宏观偏析是指宏观尺度上的溶质元素的不均匀分布，是铸造凝固过程中经常产生的重要缺陷。大型铸件和铸锭由于尺寸大，凝固时间长，宏观偏析更为严重。宏观偏析严重影响了材料的使用性能，易造成重大损失。目前普遍认为宏观偏析的形成原因主要是由于溶质富集的液相和溶质匮乏的固相之间的相对运动。这种相对运动来自于自然对流，等轴晶沉降，补缩流等多个方面［1～2］。宏观偏析的形成本质上是一个多相多尺度问题，这给宏观偏析的研究带来极大困难。数值模拟方法作为实验手段的重要补充，可以获得实验方法难以得到的数据和信息。利用数值模拟技术，可以优化工艺方案，缩短研发周期，降低生产成本。

本文建立了预测铸造凝固过程宏观偏析的数学模型。利用该模型分别对53 t钢锭和500 t铸件进行宏观偏析模拟预测，并将模拟结果和实验结果进行了比较分析。

1 数学模型

本研究宏观偏析数学模型针对凝固过程中的液相和固相分别建立守恒方程，通过界面交互关系，将两相的质量、动量、能量和溶质守恒方程紧密联系起来。模型考虑宏观尺寸上的传热、传质、流动和微观尺度上过冷、形核、晶粒长大等因素。模型中采用的基本假设如下:(1)模型中基本动力学相为固相和液相;(2)对于固相晶粒的形核采用三参数异质形核模型，而固相晶粒的生长采用溶质扩散控制的晶粒生长机制;(3)当固相分数低于临界固相分数时，固相以球状等轴晶的形貌存在，反之，则将固相视为柱状晶;(4)模型中除了动量守恒方程中的密度采用Boussinesq假设以外，固液相密度均视为相等;(5)固液相间的粘滞力采用Gidaspow模型。数学模型的控制方程如表1所示。表1中ρk、Vk、Ck、Tk分别为k相(固相或液相)的密度、速度、溶质含量和温度。

研究基于有限容积方法离散控制方程，采用多相SIMPLEC算法［3］完成凝固体系中速度-压力的耦合求解，并利用共轭梯度类方法实现离散方程线性系统的求解，实现数学模型的程序求解。

2 模型应用

2.1 53 t钢锭宏观偏析预测

图1所示为53 t钢锭几何造型示意图。该钢锭高约4 m，锭身平均直径为1.6 m。钢锭材料成分为Fe-0.41%C。模型预测钢锭完全凝固时间为15.3 h。模拟中所用物性参数等信息详见参考文献［4］。模型预测得到的53 t钢锭最终宏观偏析分布如图2所示。从图2可以看出，在钢锭底部出现负偏析区域，冒口部分则出现较为显著的正偏析。此外，在冒口区域还预测到通道偏析，这种宏观偏析模式与经典理论是吻合的［1］。

表1 数学模型控制方程Table 1 M athematic model control equation

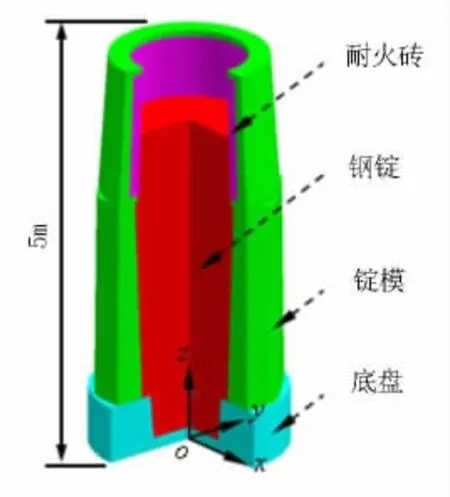
图1 53 t钢锭几何造型示意图Figure 1 Diagram of53 t ingot geometricmodel

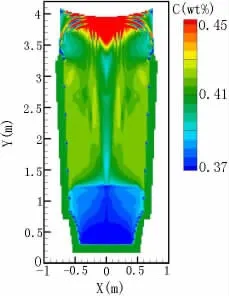
图2 53 t钢锭最终宏观偏析预测Figure 2 53 t ingot finalmacrosegregation

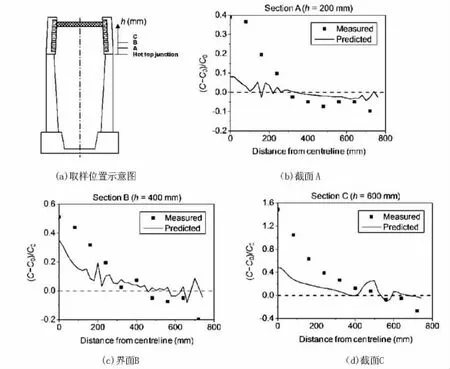
图3 53 t钢锭冒口区域宏观偏析模拟结果与实验结果的比较Figure 3 Comparison between macrosegregation and test result of 53 t ingot casting head area

模拟结果表明:等轴晶沉降是导致钢锭底部锥形负偏析区域形成的重要因素，凝固过程中形成的等轴晶发生宏观运动，部分沉降堆积于钢锭底部。从Fe-C相图可知，对于该成分(Fe-0.41%C)先析出的固相等轴晶溶质含量较低，因此在钢锭底部形成负偏析区域。

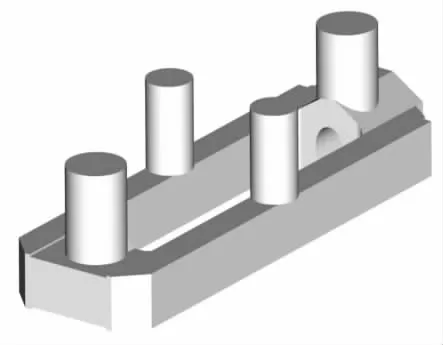
图4 500 t轧钢机架几何造型示意图Figure 4 Sketch of500 t steelmill stand model

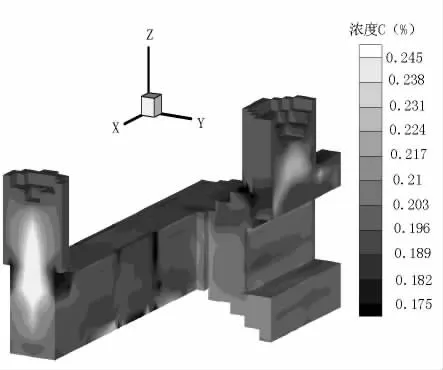
图5 500 t机架最终宏观偏析预测(1/4区域)Figure 5 500 tmill stand finalmacrosegregati on prediction(1/4 area)

图3所示为53 t钢锭冒口区域宏观偏析模拟结果与实验结果的比较。从图3可见，在三个截面上，模拟结果和实验结果定性吻合良好。从冒口中心到表面，模拟结果和实验结果呈现出由正到负的趋势，但具体数值上仍存在一定差异，无论是冒口中心区域的正偏析还是靠近表面的负偏析，预测的宏观偏析程度均小于实测。这种差异归因于数学模型中对于等轴晶形貌及运动的简化处理。

2.2 500 t铸件宏观偏析预测

图4所示为500 t轧钢机架几何造型示意图。机架三个方向最大尺寸分别为:长15 500 mm，宽4 750 mm，高2 240 mm。模拟计算中，铸件材料为Fe-0.21%C。考虑到几何对称性，模型仅对1/4区域进行计算。模拟中所用物性参数等信息详见参考文献［5］。最终凝固时刻铸件碳成分宏观偏析模拟结果如图5所示。从图5可以看出，铸件冒口顶部存在一次缩孔，冒口中心部位为碳含量最高的区域，而正偏析区下方出现低浓度负偏析区。造成这一溶质分布的主要原因是在大型铸钢件的凝固过程中，凝固顺序及固相颗粒运动相互作用的结果。凝固由底部及侧面向冒口推进，因而溶质逐渐在冒口根部富集，从而形成正偏析。同时，等轴晶颗粒在底部区域发生沉积，不但增大了所经区域的固相分数，而且降低了沉积区域的溶质浓度，随着固相颗粒不断在冒口下方的铸件中聚集，逐渐形成为负偏析区。而底部原有溶质则随着向上的流动发生上浮，也在冒口根部富集，进一步加大了正偏析的程度。模拟结果定性反映出大型铸件中的基本偏析特性。

3 结语

本文建立了预测铸造凝固过程中宏观偏析的数学模型，分别对53 t钢锭和500 t铸件进行宏观偏析数值模拟预测，模拟结果定性展现出大型铸件/铸锭宏观偏析特征模式。在此基础上，进一步对53 t钢锭冒口区域宏观偏析的实验结果和模拟结果进行比较，两者定性吻合较好，但定量上仍存在一定差异，模型需进一步细化考虑等轴晶沉降及凝固收缩等因素作用。此外，53t钢锭实测点偏少也是本研究中存在的一个问题。

本文研究工作得到了国家科技重大专项课题(2011ZX04014-131)和国家重点基础研究发展计划项目(2011CB012900)的资助。

［1］ Flemings M C.Our understanding of macrosegregation:past and present.ISIJ International，2000，40(9):833-841.

［2］ Beckermann C.Modelling of macrosegregation:applications and future needs.International Materials Reviews，2002，47 (5):243-261.

［3］ Patankar S V.Numerical Heat Transfer and Fluid Flow.New York:Hemisphere，1980.

［4］ LiWensheng，Shen Bingzhen，Shen Houfa，etal.Modelling of macrosegregation in steel ingots:benchmark validation and industrial application.IOP Conf.Series:Materials Science and Engineering，2012，33:012090.

［5］ H.Cao，H.Shen，B.Liu.Numerical Simulation of Macrosegregation during the Solidification of Steel Casting//Modeling of Casting，Welding，and Advanced Solidification Processes XI.Opio:The Minerals，Metal and Materials Society，2006: 208-215.

编辑 杜青泉

Researches on Macrosegregation Numerical Simulation during Cast Alloy Solidification Process

Tu W utao，Shen Houfa，Liu Baicheng

Macrosegregation usually occurs during the casting alloy solidification process，which greatly deteriorate the servicematerial performance.In this paper，by means of themathematic model，numerical simulation researches are conducted for the castmacrosegregation of53 t and 500 t ingots.Solidification shrinkage and equiaxial crystal settlement are considered in themodel，the simulation result is well consistentwith the test results.

cast solidification process;macrosegregation;numerical simulation

O242.1

A

2013—06—13