通货膨胀与通货膨胀不确定性：来自中国的证据

贾凯威，苏 航，任海芝

（1.辽宁工程技术大学，辽宁 葫芦岛 125105；2.辽宁大学，辽宁 沈阳 110031）

通货膨胀与通货膨胀不确定性：来自中国的证据

贾凯威1,2，苏 航1，任海芝1

（1.辽宁工程技术大学，辽宁 葫芦岛 125105；2.辽宁大学，辽宁 沈阳 110031）

以1987年1月—2013年10月为研究区间，采用两种方法对我国通货膨胀不确定性进行测度，在此基础上，对通货膨胀及其不确定性之间的关系进行了实证分析。结果表明我国通货膨胀与其不确定性之间的关系受时间长短的影响。具体地，在中短期（11个月内），通货膨胀对通货膨胀不确定性存在单向因果关系，符合Friedman-Ball假设；在长期内（12个月以上），我国通货膨胀与通货膨胀不确定性存在双向因果关系，符合Holland假设与Friedman-Ball假设。

通货膨胀；通货膨胀不确定性；VAR；GRANGER因果关系

通货膨胀作为我国宏观调控的主要目标，一直是货币当局制定与执行货币政策的重要参考变量与目标变量，也是一个充满争议的课题。一方面，通货膨胀不确定性，是影响通货膨胀成本的重要因素（Cukierman and Meltzer,1986;Karahan,2012）；另一方面，通货膨胀预期是经济决策的重要依据，而通货膨胀预期的易变性及难捕捉性影响着通货膨胀的不确定性，这就要求货币当局必须格外关注通货膨胀与其不确定性之间的关系。目前，国内外对通货膨胀与其不确定性关系的认识仍然存在分歧，有必要做进一步研究。本文的重要目的在于检验通货膨胀与其不确定性之间的关系。

一、通货膨胀与通货膨胀不确定性理论

通货膨胀及其不确定性之间的关系一直是国内外学术界的重点研究课题。目前，关于通货膨胀与其不确定性之间的关系主要有四种理论假设。

（一）Friedman-Ball假设

Okun(1971)利用OECD17个国家1951—1968年的数据首次对通货膨胀与通货膨胀不确定性间的关系进行了研究，结果表明，通货膨胀与其标准偏差间存在着正相关关系[1]。根据Okun(1971)的研究结果，货币政策在高通货膨胀期间变得越来越不可预测，因此，通货膨胀与通货膨胀不稳定性间正相关。Okun之后，Friedman(1977)在“货币政策不可预测”的假设下，对通货膨胀影响通货膨胀预期的机制进行了研究[2]。结果表明，通货膨胀上升使国内要求降低通货膨胀的呼声与诉求上升，但是决策者在治理通货膨胀上具有较大的惰性。这是因为，决策者担心紧缩性货币政策带来衰退效应。由于公众在高通货膨胀时期更难预测未来货币政策的走向，从而使高通货膨胀率导致更大的未来通货膨胀不确定性。

Ball(1992)在考虑货币当局与公众的非对称博弈的基础上，构建了一个更为正式的模型，支持了Friedman的观点。该模型假设存在两个政策决策者，一个决策者甘于忍受经济衰退以降低通货膨胀，另一个决策者持相反倾向。当经济处于低通货膨胀时，两个决策者均愿意维持当前的低通货膨胀水平。但是当经济处于高通货膨胀水平时，只有反通货膨胀决策者甘于忍受反通胀成本。因此，在高通货膨胀时期，由于公众决策者无法判断货币当局决策者是否也具有反通货膨胀的倾向与偏好，因此未来货币政策的走向充满不确定性，从而也增加了未来通货膨胀较大的不确定性，通货膨胀水平与其不确定性同向相关。自此之后，学术界将高通货膨胀导致通货膨胀不确定性增加的正相关关系称为Friedman-Ball假设。

（二）Cukierman-Meltzer假设

与Friedman(1977)及Ball(1992)不同，Cukier-man and Meltzer(1986）的研究结果表明，通货膨胀不确定性的上升，将会导致更高的通货膨胀，从而建立了与Friedman-Ball假设方向相反的Cukierman-Meltzer假设。Cukierman and Meltzer（1986）认为决策者根据时间与环境的不同随机选择其调控目标。央行倾向于要么选择通过扩张性货币政策以增加产出，要么保持较低的通货膨胀水平。随着货币供给内生性与金融创新的增强，央行对货币供给的控制力逐渐下降，从而使货币供给呈现出很大的随机性。此外，当货币当局可以自由决定其货币供给时，并不是总能够获得合适的政策工具变量。尤其是在不确定性增强的时候，由于缺少承诺机制，央行的货币政策更具有相机性与动态非一致性。此时，央行通过执行未被公众预期到的扩张性货币政策以刺激产出的激励。因此，通货膨胀不确定性导致更高的货币供给增长率，进而加剧失调通货膨胀率。学术界将通货膨胀不确定性上升所导致的通货膨胀水平上升的机制称为Cukierman-Meltzer假设。

（三）Pourgerami-Maskus假设

Pourgerami and Maskus(1987)的研究表明，通货膨胀与通货膨胀不确定性之间呈负相关关系，否定了“高通货膨胀会降低价格可预测性”论断。Pourgerami and Maskus(1987)则认为，高通货膨胀率会促使经济机构投入更多资源以提高预测精度，从而减少其预测误差。因此，通货膨胀率的上升会促使经济机构更精确地预测未来通货膨胀率，通货膨胀率与通货膨胀不确定性间存在负相关关系。学术界将该论断称为Pourgerami-Maskus假设。

（四）Holland假设

Holland(1995)认为，由于货币政策决策者具有稳定通货膨胀的动向，因此，较高的通货膨胀不确定性会降低通货膨胀的水平。Holland发现，较高的通货膨胀率增加了美国的通货膨胀不确定性，而较高的通货膨胀不确定性又降低了通货膨胀水平，这就是所谓的“稳定Fed假设”。Holland认为，央行稳定通货膨胀的动机与倾向在高通货膨胀时期会趋于增强，以降低通货膨胀不确定性产生的成本。因此，在Holland的论断中，存在一个具有较强的稳定通货膨胀倾向的决策者。通过否定Cukierman-Meltzer假设，Holland认为，通货膨胀不确定性期间的短期机会主义行为不是央行所能做出的唯一政策响应。一般情况下，货币当局更倾向于降低货币供给增长率，以此来消除通货膨胀不确定性给社会福利方面带来的负面影响。之所以这样，一方面是因为央行具有长期稳定通货膨胀的动机与倾向，另一方面，央行要受其稳定物价水平承诺机制的约束。总之，在通货膨胀不确定性较高时，央行会通过反通胀政策，以此用来降低通货膨胀的福利成本。因此，存在高通货膨胀不确定性降低平均通货膨胀水平的影响机制，学术界称该机制为Holland假设。

二、文献综述

围绕着以上观点与假设，大量的实证文献对通货膨胀与其不确定性之间的关系进行了检验，但多以发达国家为研究对象。其中，广义自回归条件异方差模型GARCH在通货膨胀不确定性的识别中得到广泛应用，GARCH模型中的条件波动率可作为不确定性的代理变量。根据Davis and Kanago(2000)的研究，工业化国家通货膨胀与其不确定性之间的关系更多地支持Friedman-Ball假设，只有少数的研究支持Cukierman-Meltzer假设。此外，几乎找不到支持Pourgerami-Maskus假设与Holland假设。

Fountas(2010)利用GARCH-M模型（将滞后通货膨胀率加入条件方差方程中）对22个工业国家通货膨胀与其不确定性之间的关系进行了研究，结果表明，通货膨胀不确定性显著地提高了通货膨胀水平，从而支持了Cukierman-Meltzer假设。Fountas et al.(2004)利用EGARCH模型对欧盟5国的研究结果表明，通货膨胀导致法国和意大利两国的通货膨胀不确定性上升，通货膨胀不确定性上升导致法国与德国通货膨胀水平的下降。Conrad and Karanasos (2005)利用1962—2001年月度数据构建GARCH模型，对美国、日本及英国的通货膨胀与其不确定性之间的关系进行了实证研究，结果表明，英国与美国支持Friedman-Ball假设，而日本则支持Cukierman-Meltzer假设。Grier and Perry(1998)利用两步法对1948—1993年G7经济体通货膨胀与通货膨胀不确定性间的关系进行了研究。首先利用GARCH模型获得条件方差作为通货膨胀不确定性的代理变量，在此基础上检验条件方差与通货膨胀的因果关系，结果表明，G7所有国家的通货膨胀均正向影响通货膨胀不确定性，从而支持了Friedman-Ball假设。此外，Fountas and Karanasos(2007)利用G7国家1957—2000年的月度数据构建单变量GARCH模型对通货膨胀与其不确定性之间的关系进行了实证检验。与以前研究不同的是，该研究用通货膨胀未预期到冲击的条件方差作为通货膨胀不确定性的代理变量，检验了通货膨胀与其不确定性之间的因果关系，结果同样支持Friedman-Ball假设。

关于单个国家的研究，Bhar and Malik(2010)利用EGARCH-M模型与双变量协整检验对美国1957—2007年的通货膨胀与其不确定性之间关系研究，结果表明，通货膨胀不确定性显著提高了通货膨胀水平，支持了Cukierman-Meltzer假设。Hwang (2001)对美国1926—1992年的研究表明，美国通货膨胀与其不确定性为弱负相关，而通货膨胀不确定性对通货膨胀的影响并不显著。因此，通货膨胀上升并不一定会增强通货膨胀不确定性。Fountas (2001)利用英国1885—1998年通货膨胀数据估计了GARCH模型，结果支持Friedman-Ball假设。

近年来，新兴经济体通货膨胀与其不确定性之间的关系逐渐成为国际关注的热点。Thornton (2007)利用标准的GARCH模型对12个新兴经济体进行了实证研究。研究结果表明，通货膨胀上升，导致通货膨胀不确定性上升，支持了Friedman-Ball假设，而通货膨胀不确定性对通货膨胀的影响并不一致。Neanidis and Sava(2011)对EU新成员的研究结果表明，大多数国家在加入EU之前，通货膨胀不确定性对于通货膨胀水平是正影响的关系，符合Friedman-Ball假设。Jiranyakul and Opiela(2010)对亚洲五国（新加坡、马来西亚、菲律宾、泰国及印度尼西亚）的研究结果表明，通货膨胀率与其不确定性同时存在双向正因果关系，从而支持了Friedman-Ball假设与Cukierman-Meltzer假设。

国内对通货膨胀与通货膨胀不确定性关系的研究最早始于王景峰和张屹山（2005）。尽管计量经济学模型与方法的不断丰富推动了该课题的不断深入，但是其结论仍然并不统一。王景峰和张屹山（2005）对我国1983—2004年间的通货膨胀特征进行了分析，基于GARCH的分析结果表明，高通胀与通货膨胀不特定性正向相关[3]。此后，刘金全等（2007）认为，我国通货膨胀一阶矩与二阶矩均存在长记忆行为，且通货膨胀水平对通货膨胀不确定性不存在显著格兰杰因果关系。陈太明（2007）的研究表明，通货膨胀不确定性与产出之间是负相关，通货膨胀不确定性与通货膨胀之间也是负相关[4]。胡日东和苏梽芳（2008）的研究表明，我国通货膨胀与其不确定性之间满足Friedman-Ball假设与Cukieman-Meltzer假设，且前者呈现U型非线性关系，后者呈现出N型非线性关系。王凯和庞震（2008）对货币供应量、通货膨胀与其不确定性之间的关系是否满足Friedman假设进行了研究，结果表明，通货膨胀加剧了我国通货膨胀的不确定性，支持了Friedman假设。苏梽芳和赵昕东（2009）在分离出长期和短期通货膨胀不确定性基础上，检验了不同期限通货膨胀不确定性与通货膨胀水平间的关系，结果表明，长、短期通货膨胀不确定性均与通货膨胀水平呈正相关，而通货膨胀对长期不确定性的影响更大。于佳和刘雪燕（2011）基于时变参数模型和时变马尔科夫模型，对通货膨胀与其不确定性之间的关系进行了研究，结果表明，通货膨胀不确定性是通货膨胀率的格兰杰原因，而货币供给的不确定性是导致通货膨胀不确定性的主要原因。陈体标和饶晓辉（2011）基于随机域回归模型及系列随机域的非线性检验结果表明，通货膨胀率引起了通货膨胀不确定性，两者呈现U型关系，支持了Friedman假说；而通货膨胀不确定性导致通货膨胀先升后降，呈现非线性倒U型关系，支持了Cukierman-Meltzer假设，在U型右侧Holland结论成立。

三、模型设计

（一）基于Arize(2000)的通货膨胀不确定性度量

采用Arize(2000)方法，按照式（1）对通货膨胀不确定性进行测度：

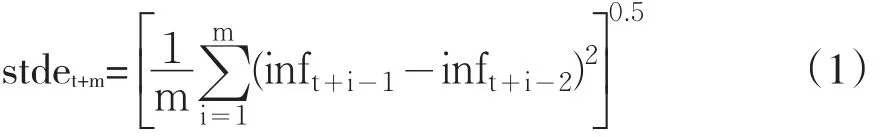
（二）基于AR-GARCH模型的通货膨胀不确定性度量

在时间序列分析中，若条件方差不满足同方差假设，而是随着历史残差与历史方差的变化而变化时，就需要用GARCH类模型进行解释。

均值方程：

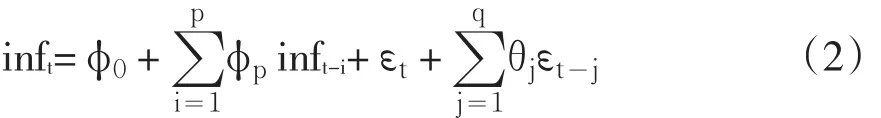
方差方程：

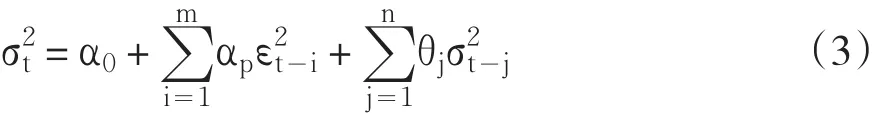
在估计GARCH方程之前，首先要对均值方程进行正确设定，这里采用标准的Box-Jenkins方法确定阶数p与q。在此基础上，估计出我国通货膨胀率的条件波动率。

（三）格兰杰因果关系检验

在测度通货膨胀不确定性stde或σ2t的基础上，进一步检验通货膨胀inf与不确定性间的因果关系及其显著性，可以得到我国通货膨胀与其不确定性关系支持哪种假说的结论，从而为我国货币政策的制定与执行提供依据。

四、实证研究

（一）通货膨胀不确定性测度

本文旨在研究我国通货膨胀与其不确定性之间的关系。根据数据可得性，这里选择我国1987年1月—2013年10月的同比CPI作为物价水平的代理变量，令通货膨胀inf=ln(CPIt-CPIt-1)。这里采用两种方法对通货膨胀不确定性进行测度，一是基于ARGARCH模型的通货膨胀率波动率测度，用GARCH波动率作为通货膨胀不确定性的代理变量；二是采用参考Arize(2000)等的做法，采用移动平均标准差来度量通货膨胀不确定性。

1.AR-GARCH模型估计及通货膨胀不确定性测度

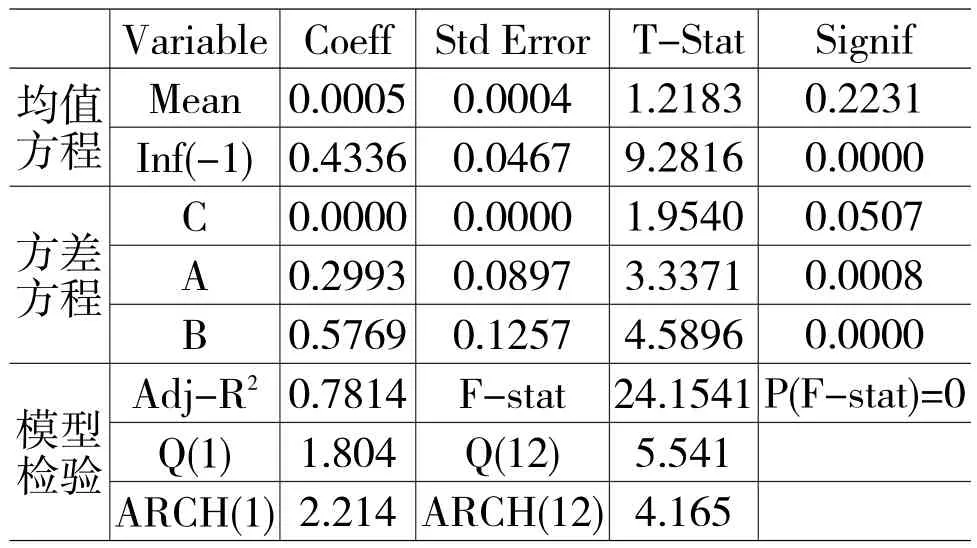
表1 AR-GARCH模型估计

从结果看，均值方程的自回归项在1%显著性水平上显著；方差方程的常数项在10%的显著性水平上显著，其余参数均在1%显著性水平上显著。从模型检验结果看，拟合优度为0.78，且残差Q检验及LM检验结果表明，模型不再存在自相关性，模型估计效果良好，提取模型的条件方差项GARCH11作为通货膨胀不确定性的代理变量，见图1。

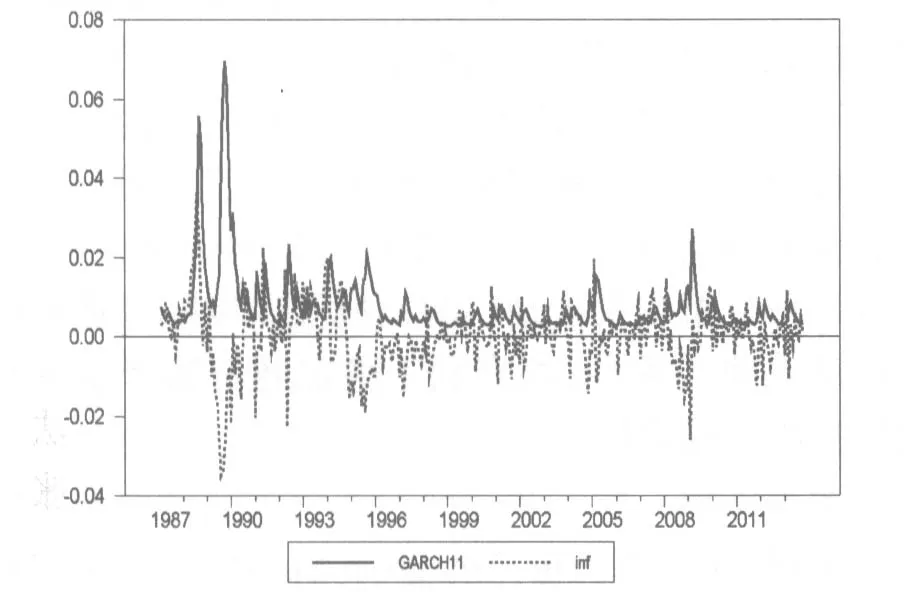
图1 通货膨胀不确定性GARCH11测度

2.基于Arize(2000)方法的通货膨胀不确定性测度

在利用GARCH模型进行通货膨胀不确定性测度的基础上，进一步利用Arize(2000)提出的样本移动平均算法测算通货膨胀的不确定性，结果见图2中的inflation uncertainty。

（二）通货膨胀inf与通货膨胀不确定性的格兰杰因果关系检验

格兰杰因果关系检验式如下：

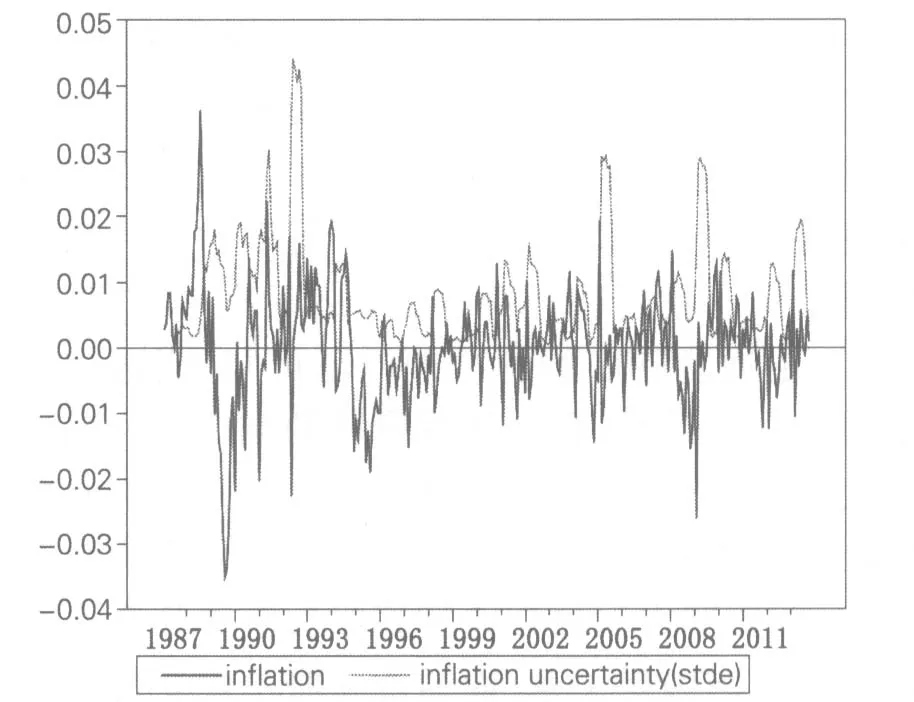
图2 通货膨胀不确定性测度(Arize,2000)

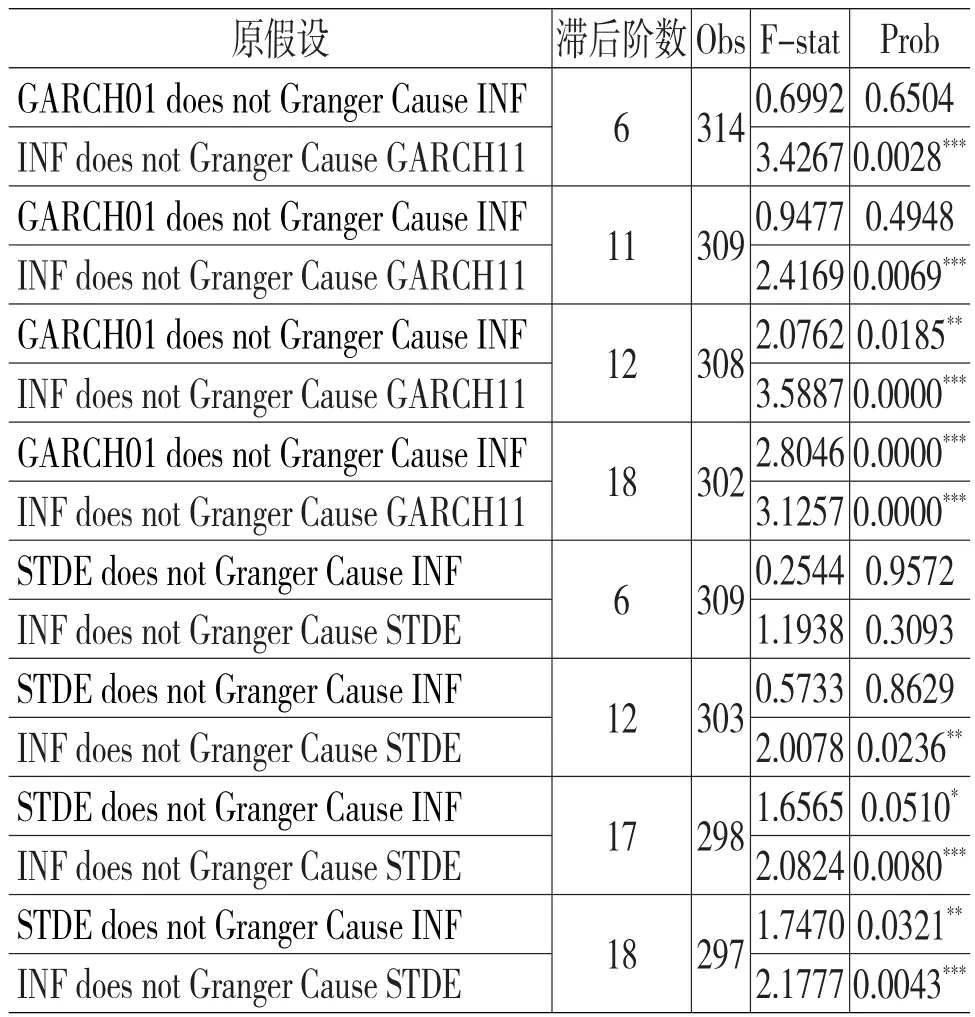
表2 格兰杰因果关系检验

检验结果表明，在滞后阶数为6—11个月的情况下，通货膨胀INF对通货膨胀不确定性GARCH11存在单向因果关系；在滞后12个月的情况下，通货膨胀INF与通货膨胀不确定性GARCH11存在双向因果关系。基于Arize(2000)的通货膨胀不确定性stde与通货膨胀INF之间的格兰杰因果关系检验结构表明，在滞后阶数为1-11时，通货膨胀与通货膨胀不确定性不存在格兰杰因果关系，在滞后阶数为12—16时，存在通货膨胀对通货膨胀不确定性stde单向因果关系；在滞后阶数超过17时，两者存在双向因果关系。综上，在长期内，我国通货膨胀与其不确定性之间存在着双向因果关系。

（三）我国通货膨胀与其不确定性计量分析——基于SVAR模型

格兰杰因果关系检验结果表明，通货膨胀与其不确定性之间长期内存在双向因果关系，这就使得传统的单方程回归技术面临着内生解释变量问题，估计结果不具有BLUE特征。VAR模型将所有变量视为内生变量，在很大程度上避免了内生变量与外生变量的识别问题。基于VAR模型的脉冲响应分析可以帮助我们理解两个变量的动态响应机制，见图3。由通货膨胀的脉冲响应图可知，当通货膨胀不确定性上升时，我国通货膨胀的响应一开始保持不变，然后下降。具体地，在前11个月内，通货膨胀INF的响应几乎为零，与格兰杰因果关系检验结果一致，即短期内仅存在通货膨胀影响通货膨胀不确定性的单向因果关系，而通货膨胀不确定性不影响通货膨胀；但是，从第12个月开始，通货膨胀出现下降趋势，到第30个月时达到波谷，符合Holland假设。从通货膨胀不确定性的响应图看，当通货膨胀上升时，通货膨胀不确定性呈现出正向响应轨迹，符合Friedman-Ball假设。具体地，当我国通货膨胀上升时，前12个月内通货膨胀不确定性只有小幅上升；但是当通货膨胀持续时间较长时，通货膨胀不确定性的上升程度急剧增大。

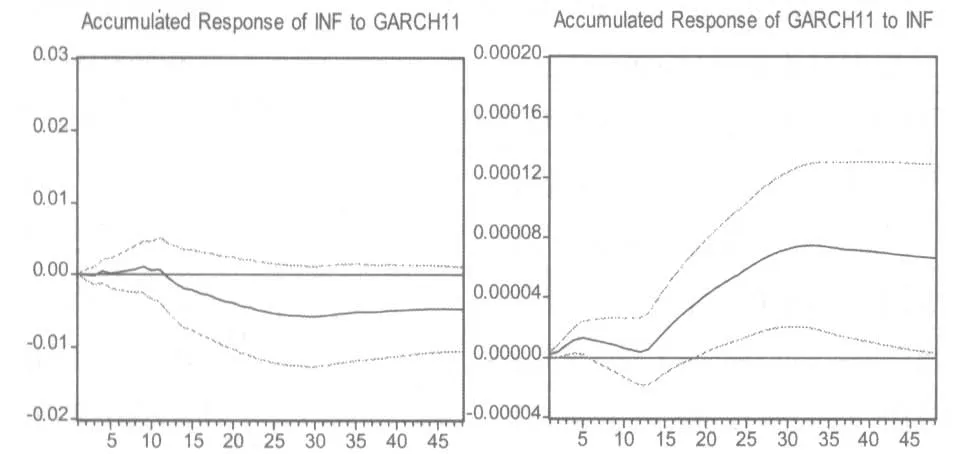
图3 脉冲响应

五、结论

第一，在中短期内，我国通货膨胀对其不确定性存在单向因果关系，符合Friedman-Ball假设；通货膨胀不确定性对通货膨胀水平的影响几乎为零。

第二，长期看（12个月以上），我国通货膨胀与其不确定性存在双向因果关系：通货膨胀不确定性导致通货膨胀水平下降，符合Holland假设；而通货膨胀上升导致通货膨胀不确定性上升，符合Friedman-Ball假设。具体地，当我国通货膨胀上升时，前12个月内通货膨胀不确定性只有小幅上升；但是当通货膨胀持续时间较长时，通货膨胀不确定性的上升程度急剧增大。公众的通货膨胀预期能够解释这一现象。在短期内（12个月内），货币当局对通货膨胀的应对措施具有滞后性，且货币当局缺少调控通货膨胀的倾向与偏好，使未来通货膨胀具有较大的不确定性。伴随着通货膨胀持续时间的增长，公众对货币当局治理通货膨胀的积极性与能力产生置疑，从而导致更大的通货膨胀不确定性。

由此可见，我国通货膨胀与其不确定性之间的关系受时间长短的影响。第一，短期内，仅存在通货膨胀影响通货膨胀不确定性的单向格兰杰因果关系；长期内，通货膨胀与其不确定性存在双向格兰杰因果关系。第二，短期内，通货膨胀不确定性对通货膨胀的影响几乎为零；长期内，通货膨胀不确定性将导致通货膨胀水平下降。这表明，短期内不确定性增强的时候，央行的货币政策具有相机性与动态非一致性。央行具有通过执行未被公众预期到的扩张性货币政策以刺激产出的激励。但是在长期内，“保民生、控通胀”使货币当局具有控制通货膨胀的动机与倾向，反映了我国央行货币政策调控的重点逐渐转向维持物价稳定上。第三，尽管通货膨胀对通货膨胀不确定性的影响符合Friedman-Ball假设，但是在短期内，通货膨胀上升导致通货膨胀不确定性小幅上升，在长期内，上升幅度增加。这表明，通货膨胀水平上升时，短期内公众对通货膨胀预期基本一致，但是随着通货膨胀水平的上升，公众预期出现分化，增加了通货膨胀的不确定性。

综上，增强货币政策制定与执行的透明度，强化央行对物价水平目标的承诺机制，实施预期管理，加速利率市场化，逐渐从数量型调控转向价格型调控，尝试某种货币政策规则（如泰勒规则）以降低货币政策的动态非一致性，均有利于稳定通货膨胀水平及通货膨胀不确定性。

[1]Okun A M.The Mirage of Steady Inflation[J]. Brookings Papers on Economic Activity,1971,1971(2): 485-498.

[2]Friedman M.Nobel Lecture:Inflation and Unemployment[J].The Journal of Political Economy, 1977:451-472.

[3]王景峰，张屹山.我国转轨时期通货膨胀特征实证分析[J].当代经济研究，2005，（2）：49-52.

[4]陈太明.不确定性、通货膨胀与产出增长[J].经济理论与经济管理，2007，（12）：23-27.

（责任编辑：王淑云）

1003-4625（2014）09-0042-05

F820.5

A

2014-07-11

本文为国家科技支撑计划资助项目(2013BAH12F01)；辽宁省教育厅科学研究一般项目（批准号：W2012047）。

贾凯威（1980-），男，河北保定人，经济学博士，统计学博士后（在站），讲师，研究方向：计量经济学模型与应用；苏航（1989-），女，辽宁朝阳人，工商管理硕士研究生，研究方向：决策理论与方法；任海芝（1966-），女，辽宁阜新人，博士，教授，研究方向：决策理论与方法。