一类群居捕食者的捕获系统的定性分析

华极鑫，冯维龙，姜玉秋

(吉林师范大学数学学院，吉林四平 136000)

一类群居捕食者的捕获系统的定性分析

华极鑫，冯维龙，姜玉秋

(吉林师范大学数学学院，吉林四平 136000)

本文建立了捕食者是群居种群的捕食者-食饵系统，分析了密度大小对群居捕食者种群增长的促进和抑制作用，并且对其平衡点的稳定性进行了系统的研究。

群居；捕食者-食饵系统；密度；平衡点；稳定性

1 建立模型

考察生存在同一理想环境中的捕食者和食饵种群.Volterra捕食者-食饵[1]结构为：

(1.1)

在此基础上建立了群居捕食者-食饵的数学模型

(1.2)

其中a1，a2，b1，b2，c1均为正常数.本文将对系统(1.2)进行定性分析.

2 系统分析

将系统(1.2)改写成

(2.1)

其Jacobi矩阵为

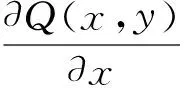
(3)而且你底妹妹对我的情义,叫我用什么来接受呢?心呢,还是两手?我不能拿理智来解释与应用的时候,我只有逃走之一法。

令Δ=a11a22-a12a21,δ=-(a11+a22).

定理2.2 平衡点o(0,0)为鞍点.

证明 首先证明正平衡点E(x*,y*)的存在性与惟一性.

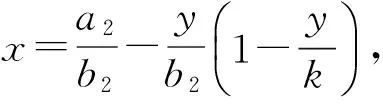
下面证明E(x*,y*)是局部稳定的.

当k<3a2时，Δ>0,δ>0，可知E(x*,y*)是局部渐进稳定[5]的.

证明 由定理2.4知，正平衡点E(x*,y*)是局部稳定的，又由文献[6]中全局稳定性给出的定理2.2及推论2(有详细证明)，可知E(x*,y*)是全局渐近稳定的.

3 生物学意义

通过对系统(1.2)的分析讨论，我们可以找到群居捕食者和食饵最适合生存的数量E(x*,y*)，利用密度对群居捕食者的作用，控制捕食者或食饵数量来维持生态平衡，当食饵种群繁殖较快时我们可以通过人为引入群居的捕食者来控制其增长速度，而不用担心捕食者数量会肆意增长，两种群数量达到y*，x*时，就可以达到生态平衡稳定，从而实现保护珍稀物种、抑制那些繁殖过快而又有害的种群的目的.

[1]马知恩,周义仓.常微分方程定性与稳定性理论[M].北京:科学出版社,2001.

[2]尚玉昌.普通生态学[M].北京:北京大学出版社,2002.

[3]姜玉秋.Turchin-Batzli捕食者-食饵系统的定性分析[J].东北师范大学学报:自然科学版,2006,38(4):17-21.

[4]程荣福,赵明.一类捕食者与被捕食者模型的持久性与稳定性[J].生物数学学报,2008,23(2):289-294.

[5]王希超,王志斌,徐胜荣.一类捕食-食饵系统的定性分析[J].生物数学学报,2009,24(2):287-292.

[6]马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996.

Qualitative Analysis of a Kind of Gregarious Predators Capture System

HUA Ji-xin,FENG Wei-long,JIANG Yu-qiu

(College of Mathematics, Jilin Normal University, Siping Jilin 136000, China)

In this paper, gregarious predators Prey-Predator system was established, and positive and negative density effects of gregarious predators growth was analyzed. Moreover, the stability of the equilibrium point was system studied.

gregarious; Prey-Predator system; density; equilibrium point ; stability

2013-11-13

华极鑫(1989- )，女，吉林松原人，吉林师范大学数学学院硕士研究生，从事生物数学研究。

姜玉秋(1966- )，女，吉林师范大学数学学院教授，硕士生导师。

O175

A

1008-178X(2014)01-0004-03