圆孔孔边的应力集中分析及优化

闫思江，曾显波，李凡国，陈春光

（青岛港湾职业技术学院 机械系，山东 青岛266404）

0 引言

在圆孔附近的局部区域内，应力急剧增大，而在离开这一区域稍远处，应力迅速减小而趋于均匀，这种由于几何形状改变而引起的应力局部增大的现象称为应力集中。应力集中与孔径大小无关，而与孔的几何形状有关[1]。应力集中现象将一直保持到最大局部应力到达强度极限之前。因此，在设计构件时，应考虑应力集中的影响。为避免应力集中造成构件的疲劳破坏，改进措施主要是改善构件外形以降低应力值[2]。本文通过优化方法，对于不同的应力约束要求，给出合理的几何形状。

1 理论分析

如图1 所示，一弹性矩形薄板受集度为q 均匀拉伸作用，板中心有一孔径为2a 的圆孔，板厚为1，坐标原点取在圆孔中心，坐标平行于边界。

由于讨论圆孔孔边的应力集中问题，宜采用极坐标。首先将外部直边界变换为圆边界，为此作如下等代变换：以圆点O 为圆心，以远大于a 的长度b 为半径作一大圆。根据应力集中的局部性，在大圆的周边上任一点A 处的应力与无孔时相同，即σx=q，σy=τxy=0。应用坐标变换公式，可得A 点的极坐标分量：

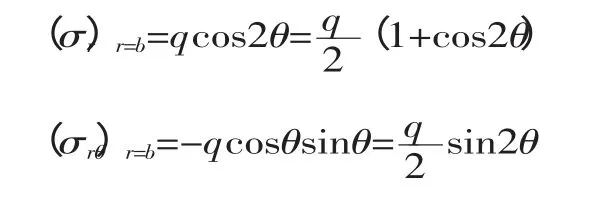
于是矩形板转换成了内半径为a、外半径为b的厚壁圆筒的一个截面，根据参考文献[1]可以得到圆孔孔边的应力计算公式：

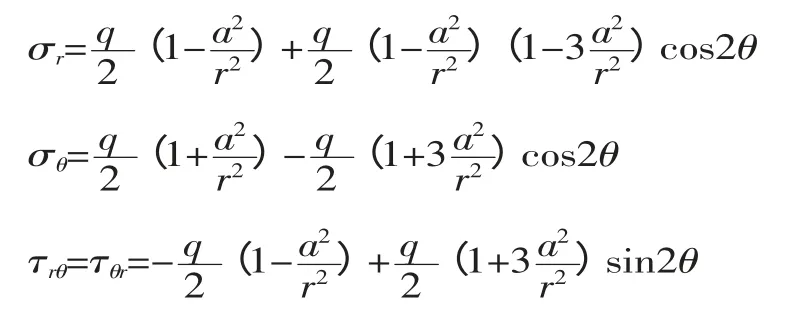
根据上述公式可以得到如下结论：

（1）沿孔边（r=a）的环向应力和径向应力：

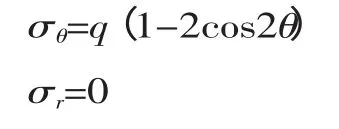
（2）沿y 轴（θ=±π/2）的横截面面上的环向应力：

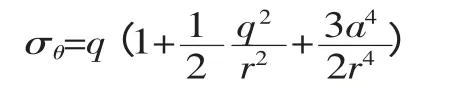
（3）沿y 轴（θ=0，π）的的横截面面上的环向应力：

（4）孔边最大应力出现在θ=±π/2 处，最小应力出现在θ=0，π 处，即

2 有限元分析

试样为200×120mm2，厚度1mm 板，中心孔直径12mm，划分为76840 个四边形网格，施加集度q=1的载荷，参见图1。

采用HyperWorks 软件的Radioss 求解器，对圆孔孔边应力进行有限元分析，具体步骤为：①建立有限元模型，在孔边采用局部细化技术，加密网格以提高计算精度；②设置材料参数；③设置属性；④加载，为便于观察，设置加载集度q=1；⑤创建工况；⑥提交求解。

计算结果如图2 所示。从图中可以看出最大应力发生在θ=±π/2 处，最小应力出现在θ=0，π 处，计算结果与理论值吻合的很好，其准确度见表1。所出现的误差与单元网格划分精细程度有关。由于精度比较高，为下面的自由形状优化奠定了可信赖的基础。

图2 孔边应力分布图

表1 孔边最大、最小应力值

3 自由形状优化

应力集中的程度越高，集中的现象越是局部性的。由于最大应力值与孔径无关，只与几何形状有关，因此在构件中挖孔或留孔，应充分重视挖何种形状的孔。不同的几何形状有不同的应力集中。

自由形状优化的目的为改变某一区域的几何形状，并要求满足一定的约束，以提高结构特性。为避免应力集中过高，尤其是脆性材料承受交变应力载荷情况下[3]，通过实验及检测试样是不经济的，既耗时又浪费，而目前又没有基于力法的理论解，为此使用基于矩阵位移法的有限元方法对圆孔孔边进行自由形状优化，可以为疲劳分析提供理想的几何形状。

自由形状优化的基本思想与其他形状优化技术不同的是，其边界节点的移动由软件自动确定，不需要人工定义节点扰动。结构的形状改变被定义为扰动矢量的线性组合。扰动矢量用于定义与原始网格相关节点位置的改变，设计变量为扰动矢量的系数，即

式中：X——节点坐标矢量；

X0——节点设计初始时的坐标矢量；

PVi——与设计变量DVi相关的扰动矢量[4]。

比较目前各种通用的有限元软件，针对自由形状优化HyperWorks 软件的Optistruct 模块最为突出。其步骤为：①前述应力分析步骤第1 步～第5 步；②使用free shape 选择圆孔边上的所有节点将其作为自由形状优化变量DV；③使用Responses，创建应力响应Stress，应力类型选择Von Mises，同时考虑单元的两面；④创建体积响应Vol 作为优化目标，类型设置为Volume；⑤设置应力约束Dostress，使用不同的约束产生不同的几何形状；⑥以体积（质量）Vol 作为优化目标，使之最小；⑦创建工况Loadstep；工况可以是多种载荷或载荷叠加，这里为了说明方法仅采用单一的均布拉伸载荷；⑧提交求解。

考虑到前面应力分析所得到的σmax=3.043q，在创建应力约束时，设置应力约束σmax≤2.5q，进行优化得到的应力分布图和位移图如图3、4 所示。

由图3 可以看出，孔周围应力最大为2.5q；而图4 给出了相对应的几何外形，即只要将y 轴方向直径减少2×0.83=1.66mm，而x 轴向直径不变即可，也就是说构件上的孔，挖成图4 给出的几何形状，在相同载荷作用下，最大应力值不会超过2.5q。

图3 最大应力小于2.5q 应力分布图

图4 最大应力小于2.5q 位移图

图5 最大应力小于2q 位移图

图6 最大应力小于1.5q位移图

图7 最大应力小于1.2q位移图

图5、6、7 分别为将最大应力降至2.0q、1.5q、1.2q 以下时的位移图，由于观察几何形状，这里没有给出对应的应力分布云图。可以看出横向尺寸越小，应力集中越小。中心区域即为对应不同应力大小要求孔的理想几何形状。也就是说，只要按位移图给出的形状加工孔，最大应力不会超过相应的最大应力值。孔边的几何坐标值可从结果文件中直接导出到Excel 文件中，这样可直接使用这些数据进行数控加工，非常方便。

4 结论

（1）基于HyperWorks 平台，对应力集中分析，只要单元划分的足够细，具有很高的精度。

（2）所述方法虽然是对圆孔孔边进行的分析，可将其推广到任意形状的应力分析过程中，以获得相应的几何外形，不受任何限制。

（3）优化方法步骤简单明了，可为今后的疲劳分析物理实验提供可靠的几何形状依据。

（4）在单向受力情况下，应尽量使受力方向几何尺寸大于横向尺寸，即横向尺寸越小应力集中程度越低。

[1]徐芝纶.弹性力学[M].北京：高等教育出版社，2008.

[2]蒋玉川.弹性力学与有限元法[M].北京：科学出版社，2010.

[3]徐镇宇，等.机械零件[M].北京：人民教育出版社，1981.

[4]洪清泉.OptiStruct & HyperStudy 理论基础与工程应用[M].北京：机械工业出版社，2013.

[5]闫思江，李凡国.超声波疲劳试验谐响应分析[J].锻压装备与制造技术，2011，46（6）：87-89.

[6]李凡国，赵剑波，闫思江.基于MSC.MARC 的TP2铜管材液压胀形数值模拟[J].锻压装备与制造技术，2013，48（6）：95-97.