大体积混凝土施工过程温度控制研究及其实践
龙勇彪,陈黎明
(1.湖南交通国际经济工程合作公司,湖南长沙 410011;2.湖南省溆怀高速公路建设开发有限公司,湖南怀化 418000)
0 引言
随着国家基础建设的迅速发展,桥梁工程的建设也取得了迅猛的发展,桥梁的跨越能力在不断的增大,出现了若干跨越海峡的特大型桥梁。由于桥梁在朝着特大跨度发展,必然对桥梁的结构形式提出更高的要求。其中的一个表现就是桥梁结构的设计和施工中越来越多地应用到大体积混凝土这一结构形式,如:单跨拱桥的拱脚结构、预应力连续刚构桥的0号块,斜拉桥的桥塔以及地锚式悬索桥(该结构具有极为强大的跨越能力)的锚碇构造等等都是大体积混凝土结构。这些构造都是相关结构的主要受力部分,其施工质量直接关系到结构在施工过程以及成桥运营阶段结构的安全。但是,上述大体积混凝土结构在施工过程中暴露出很多问题,其中比较常见的一个问题就是大体积混凝土在施工过程中的开裂问题[1]。相关混凝土配合比设计规范规定:结构实体最小尺寸不小于1m的混凝土结构即可称之为大体积混凝土结构。国外规范则规定:在施工过程中会因温度的影响而开裂的结构可视为大体积混凝土结构。目前,国内外对外力作用下引起的混凝土开裂问题研究较多也比较透彻[2]。但对由温度荷载引起的结构开裂问题的研究较少,对于桥梁结构中大体积混凝土的开裂问题更应该引起设计和科研人员的足够重视,进而总结出防止危害结构裂缝的产生的方法。基于此,本文以某地锚式悬索桥结构的锚碇为工程背景,在理论研究与计算及裂缝开裂机理分析的基础上,提出了在施工过程中预防结构由于温度作用下开裂的措施。通过理论计算和实测数据的分析,表明本文提出的大体积混凝土施工过程的温控方法是可行并有效的,能够为类似结构的设计和施工提供参考。
1 大体积混凝土温度计算理论概述
1.1 计算结构温度效应的热传导方程
先假定某一各向同性、材质均匀并且处于线性弹性状态的固体,从中取出一微小六面体dxdydz(用于理论研究的微元),如图1所示。对该微元体考虑在单位时间内从左界面流入的热量为qxdydz,从右界面流出的热量为qx+dxdydz,在该单位时间内流入该微元体的净热量则为(qx-qx+dx)dydz。
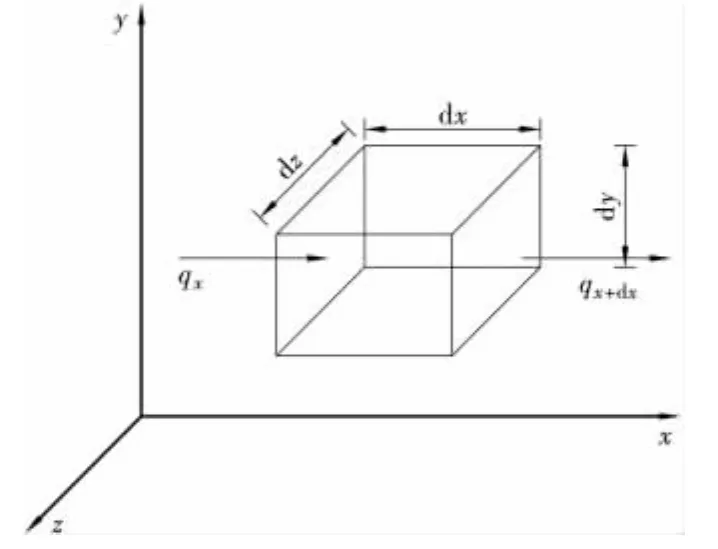
图1 微小六面体
基于热传导原理并遵循傅里叶定律,同时假定由微元体吸收的造成温度升高的热量必须等于从外界流入的净热量和由于结构在水化反应过程中所释放的水化热之和的基本假定可得[3]:
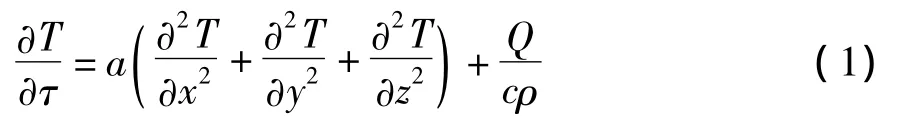
式中:a为导热系数,a=λ/cρ,m2/h;Q 为热量,J;τ为时间变量。
上式即为用于结构热力学计算的热传导方程。若考虑结构处于绝热条件下,则可得到绝热条件下的热传导方程。若温度沿某个坐标方向是常数,可得到热传导方程的二维表达式;若温度沿任意两个坐标方向是常数,可得到热传导方程的一维表达式;如果温度不随时间变化(恒温条件),即温度变化只是空间坐标的函数而与时间变量无关,在这种不随时间变化的稳定温度场中可得到热传导方程在恒温条件下的表达式。
1.2 解答热传导方程的初值条件与边界条件
表达式(1)所示的热传导方程建立起了混凝土结构体的温度与空间坐标及时间的关系,但是该方程存在无穷多解,只有附加上初始条件和边界条件,才能通过微分方程的求解方法得到上述热力学方程的唯一解答,从而确定作用于结构上的温度场,所用的初始条件和边界条件称为定解条件。1.1中的热传导方程只有在已知大体积混凝土结构物内部最初时各点的温度分布情况(初始条件)及结构的表面与周围环境中的介质(空气、水及岩土等)之间的相互热作用规律(边界条件)才能求得唯一解得温度在结构物内部的分布规律及其随时间的变化规律。一般情况下,混凝土与周围岩土以及现浇与后浇混凝土接触面上的初始时刻温度是不连续的。求解结构物温度分布的边界条件分为如下4种[4]:
1)第一类边界条件是指结构的表面温度可通过时间的已知函数来表达,当混凝土与水接触时,其表面温度等于水温,属于此类边界条件。
2)第二类边界条件是指结构表面的热流量可通过时间的已知函数来表达。
3)第三类边界条件则是指物体边界上热流量平衡条件,该条件运用混凝土表面温度T和大气温度Ta之差来线性表示通过混凝土表面热流量,也就给出了结构与周围环境之间相互传热所满足的条件。此类边界条件被广泛运用于混凝土结构物中。
4)第四类边界条件:对于相互接触的两个固体,如接触面良好,则热流量和温度在接触面上都是连续的。反之,热流量和温度在接触面上不连续。
在热传导方程以及相关的初值条件与边界条件的基础上,再结合混凝土的热性质、水泥水化热以及混凝土的绝热温升等基本的材料热力学参数,就可运用有限单元方法对结构在温度下的热力学响应进行计算[4]。
2 大体积混凝土施工过程温度裂缝形成机理及防治措施
2.1 大体积混凝土开裂原因及温度应力的形成机理
工程中引起混凝土结构中产生裂缝的原因有多种,首先可能是结构的设计不合理造成结构在荷载(主要是恒载)作用下的受力裂缝(如箱梁施工过程中副腹板在剪应力作用下的开裂);另外,施工过程中模板刚度不合理而产生的变形以及基础不均匀沉降也会造成结构的受力变化而引起开裂。其次,混凝土结构在施工过程中也可能产生非受力裂缝,这种裂缝一般称之为构造裂缝,造成混凝土构造性开裂的主要原因有多种:结构内部温度分布不均匀,混凝土结构表面温度的迅速变化,混凝土初凝后内部湿度的变化,混凝土材料本身的脆性和不均匀性,水化反应过程中的碱骨料反应等。
对于大体积混凝土这一结构而言,在施工过程中,由于混凝土硬化期间的水化反应过程要放出大量水化热,结构内部温度上升速度较快,但是结构表面附近的温度的增长比较滞后,因此会造成结构温度分布不均匀从而在表面产生拉应力;与此同时,结构表面气温的降低也会在混凝土表面引起较大的拉应力。此外,在大体积混凝土强度发展后期的降温过程中,由于基础以及已浇筑混凝土对新浇筑混凝土的约束作用,也会使得混凝土内部出现拉应力。在钢筋混凝土中,拉应力主要是由钢筋承担,混凝土只是承受压应力。在素混凝土内或钢筋混凝土的边缘部位如果结构内出现了拉应力,则须依靠混凝土自身承担。当这些位置拉应力如果超过混凝土抗拉强度时就将造成混凝土结构的开裂,从而出现裂缝。
混凝土在强度形成过程中温度应力的形成过程可分为以下3个阶段:①早期:自浇筑混凝土开始至水化反应放热基本结束,该阶段特征主要是水泥放出大量的水化热及混凝上弹性模量的急剧变化。②中期:自水泥放热作用基本结束时起至混凝土冷却到稳定温度时止,这个过程中,温度应力主要是由于混凝土的冷却及外界气温变化所引起。③晚期:混凝土完全冷却,此时的温度应力主要是外界气温变化所引起。每一阶段结束时的结构应力都为该阶段和此前所有阶段的应力的叠加。
2.2 施工中防止大体积混凝土开裂的措施
根据2.1中的混凝土温度应力形成及开裂机理分析,为了防止混凝土因温度应力的发展而引起开裂,可以从控制结构的温度变化、改善约束条件及改善材料性能等三个方面采取措施。
控制温度的措施如下:①改善骨料级配,采用干硬性混凝土并掺加混合料(如引气剂或塑化剂等)以减少水泥用量;②拌合混凝土时用水将碎石冷却以降低混凝土的入模温度;③热天采用分层浇筑的方法(控制浇筑厚度)使得浇筑完的混凝土有充分的散热时间;④在混凝土中埋设冷却水管,利用通入水管中的冷水带走水化反应过程所释放的部分热量;⑤应该控制好拆模时间(不应过早),气温骤降时应该注意结构表面的保温,防止因混凝土表面温度的骤降而开裂;⑥寒冷季节应该注意施工中长期暴露的混凝土表面的保温。
改善约束条件的措施是:①合理设置施工缝以及后浇带等可以防止由于施工进度引起的结构开裂;②避免基础过大起伏;③合理的安排施工工序,避免过大的高差和侧面长期暴露。
改善混凝土材料性能的措施:① 由于水灰比是影响混凝土收缩的重要因素,使用减水剂可减少混凝土水化反应过程用水量。②水泥用量也会影响到混凝土的收缩,掺加减水剂可使混凝土在保证强度的条件下可减少水泥用量,而用骨料来保证结构的体积。③混凝土抗裂性能的提高可通过提高水泥浆与骨料的粘结力来实现。④减水防裂剂可有效提高混凝土抗拉强度,以此提高其抗裂性能。⑤掺加减水防裂剂后混凝土缓凝时间适当,在有效防止水泥水化时迅速放热基础上,避免因水泥长期不凝而带来的塑性收缩增加。
综上,鉴于防止混凝土裂缝的产生是保证混凝土施工质量的重要环节,在施工过程中,应该从上述各个方面采取措施来保证混凝土强度形成过程中不出现开裂的情况,尤其应该注意避免结构产生贯穿裂缝,此种裂缝一旦产生将严重破坏结构的整体性。
3 某地锚式悬索桥锚碇施工过程温度效应分析及温控实践
3.1 工程概述及施工中采取的温度控制措施
本文以某地锚式悬索桥锚碇结构的施工过程为背景来研究大体积混凝土施工过程中的温度控制问题。该桥是某高速公路的控制性工程,其结构形式为单跨简支钢桁架地锚式悬索桥,跨径布置为(200+856+190)m,桥梁两岸各设一个锚碇作为主缆的锚固构造物,其中一个锚碇高为29m,采用C30混凝土,分17层浇筑,平面最大尺寸为30.5m×56.7m。显然,该重力式锚碇为大体积混凝土结构。见图2。
在锚碇施工的整个过程中运用温度传感装置对该大体积混凝土结构的混凝土浇筑过程进行温度实时监测。施工过程中,对混凝土的浇筑过程所采取温度控制措施,如:在混凝土拌和物中添加粉煤灰,对锚碇构造进行分层浇筑并在每一结构层都布置冷却水管,防止混凝土内部应水化反应放热而积蓄大量热量来防止局部高温,以此实现混凝土内部温度控制[5]。
3.2 考虑浇筑过程实际情况的大体积混凝土温度效应实测值分析及其与理论值的比较分析
笔者对混凝土实际浇筑过程中结构的温度变化情况进行了实时监测,由温度实测数据绘出锚碇右幅第1层和第3层锚块混凝土的龄期—温度曲线图如图3、图4所示,实测数据曲线分析如下:
1)从图3、图4各测点的变化曲线可以看出:各层混凝土内部温度变化走向大致相近,不同时间的浇筑区段达到温度峰值和温度开始下降的时间基本相同,这就意味着可同时开启或者停止冷却水的循环。同时也说明两图中的温度变化曲线能反映出大体积混凝土结构在水化反应过程中温度变化的实质。
2)该大体积混凝土锚碇各层均为一次性浇筑完成。由于混凝土的导热系数小,且结构底部和四壁的散热量也很小,该结构的散热可近似视为一维散热,从图3、图4曲线可以看出,温降曲线呈平缓下降趋势。
3)图3、图4显示,该大体积混凝土锚碇的水化热温度峰值大都在混凝土浇筑完成后的3d左右出现,这主要是因为混凝土水泥用量较低以及拌和物中粉煤灰和缓凝减水剂的使用。这就说明粉煤灰可以起到降低温度峰值的作用;缓凝减水剂使水泥的前期水化速率减慢,使得水化热量充分散失,从而使水化热引起的温度峰值较低。
4)图3、图4显示,由于受外界环境温度的影响,结构表面温度波动较大,由此可以看出对结构表面保温的重要性。考虑到混凝土的导热系数较小,结构中部和底部温度变化平稳,中部的降温速率比底部小。由此可见大体积混凝土主要依靠混凝土表面散热,而中部区域主要依靠冷却水散热。
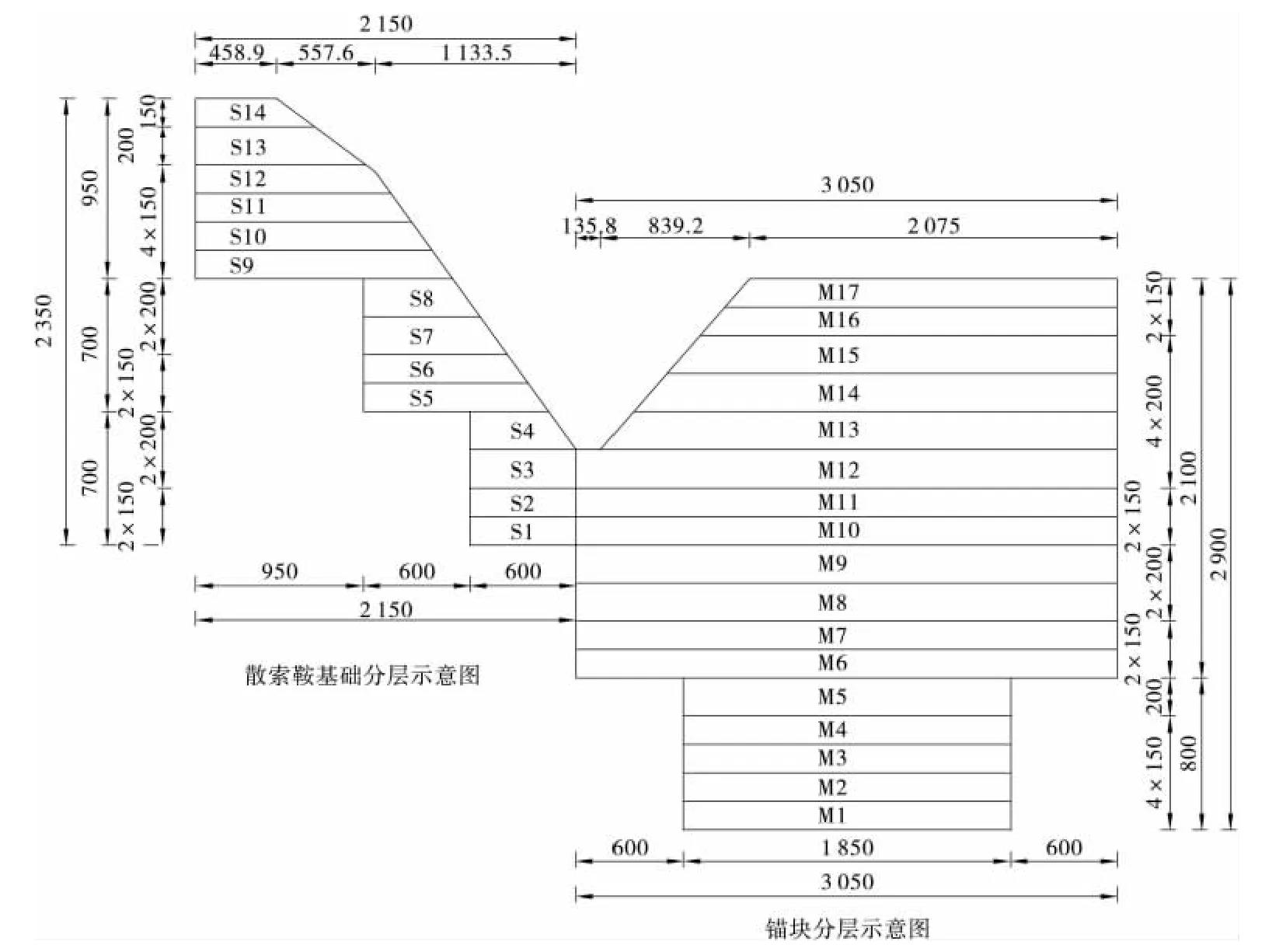
图2 花垣岸锚碇分层浇筑图(单位:cm)
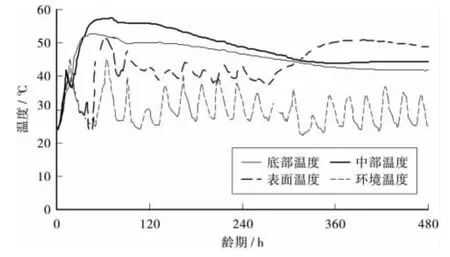
图3 锚碇右幅第1层锚块典型温度曲线
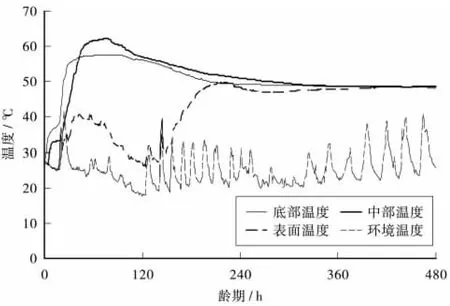
图4 锚碇右幅第3层锚块典型温度曲线
考虑浇筑过程实际情况得到的混凝土理论温度状态及应力状态与实际状态比较分析如下:
在得到准确的大气温度、混凝土入模温度、冷却水管通水流速等参数后,就可以按照外界条件及结构的实际情况对结构在浇筑过程的温度变化情况及结构在温度作用下的反应进行有限元模拟和理论计算分析。如图5~图7所示。有限元计算结果表明,浇筑过程结构的最高温升为32.42℃,能满足混凝土抗裂要求。同时,有限元分析表明,在采取添加粉煤灰和对锚碇构造进行分层浇筑并在每一结构层都布置冷却水管等措施的前提下,混凝土在浇筑过程中因内外温度作用所表现的拉应力为0.83~1.63MPa,小于混凝土相应龄期的抗拉强度。
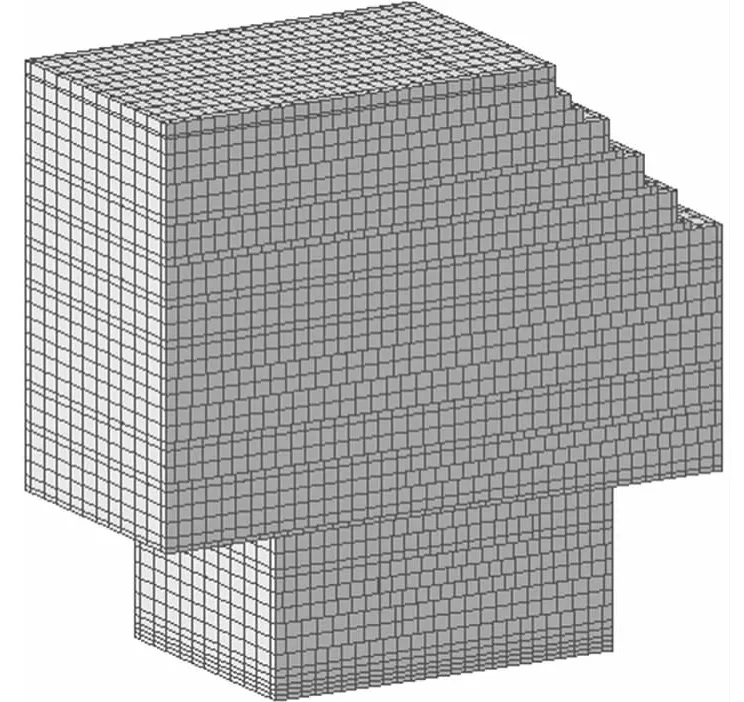
图5 锚碇有限元模型图
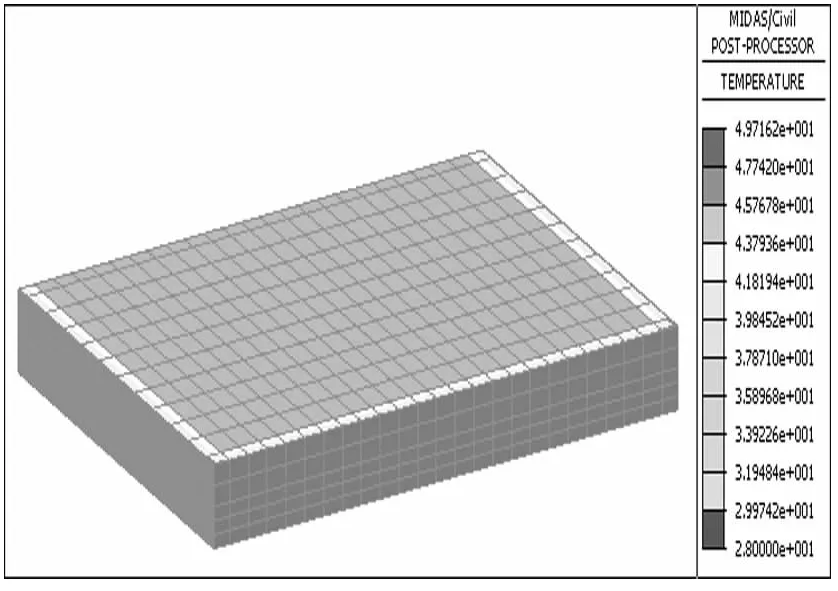
图6 第1层锚块混凝土出现最高温度时温度云图
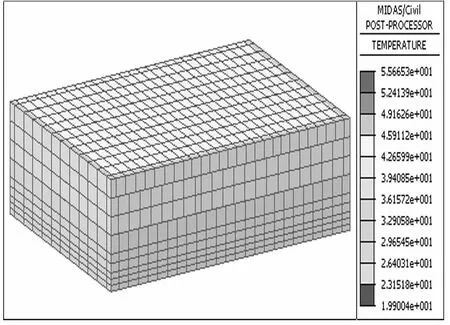
图7 第3层锚块混凝土出现最高温度时温度云图
理论计算数据和实测数据表明,按照施工过程实际情况进行模拟得到的最高温度为56.5℃,而实测最高温度为63.4℃,两者差值为11%,理论与实际有一定差距,其原因主要存在与模型边界条件模拟的准确度,模型冷却水流参数以及混凝土本身参数(绝热温升等)与实际情况的差异等。但是,最高温度的理论与实测值还是比较接近,说明混凝土在浇筑过程中内部的理论应力状态能基本反映混凝土在浇筑过程中的实际应力状态,如果理论拉应力满足规范要求则可认为结构实际应力也满足规范要求。这就表明在采取温控措施的条件下,混凝土内部各点的拉应力不会引起混凝土的开裂,从而实现混凝土在浇筑过程中的质量控制,也就证明本文采取的大体积混凝土温控措施是可行的。
4 结语
1)本文在介绍热传导方程和解这个方程的若干种边界条件的基础上,提出了运用有限元进行大体积混凝土结构温度效应分析的计算方法。
2)对大体积混凝土施工过程进行温度控制有它的客观必要性,本文从防止混凝土由温度引起裂缝的机理出发,说明了对这种结构进行施工过程温控的必要性。
3)通过对混凝土浇筑过程和强度形成过程的温度实测数据分析表明,在拌和物中掺加粉煤灰缓凝减水剂以及向结构内部通入冷却水的措施,能够保证混凝土内部水化热的及时散失,以保证结构内外温度均匀,防止混凝土因受热不均匀而开裂。
4)本文提出了对大体积混凝土施工过程进行温度控制的基本方法,并对混凝土浇筑的早期和中期的内力状态进行了有限元仿真分析,考虑浇筑过程实际情况得到的混凝土理论应力状态与实际状态(实测数据)比较分析表明:混凝土在强度形成过程中,如果采取相应的温控措施则基本能够保证结构不出现裂缝,同时也证明本文温控方法是可行的。
[1]朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1998.
[2]王铁梦.工程结构裂缝控制[M].北京:中国建筑工业出版社,1997.
[3]张洪济.热传导[M].北京:高等教育出版社,1992.
[4]孔祥谦.热应力有限单元法分析[M].上海:上海交通大学出版社,1999.
[5]朱岳明,徐之青,严 飞.含有冷却水管混凝土结构温度场的三维仿真分析[J].水电能源科学,2003,21(1):83-85.

