基于粘弹性边界的路基路面动力响应及沉降分析

卢山东

(湖南省溆怀高速公路建设开发有限公司，湖南怀化 418000)

对于含地基结构分析，我们往往只对结构周围局部地基区域感兴趣，故在数值分析过程中，一般在半无限地基介质中截取有限的计算区域，并在该区域的边界上设置人工边界来等效近似。

人工边界可以分为局部人工边界和全局人工边界两大类［1］。局部人工边界计算时间短，效率高，因而比全局人工边界更受欢迎。目前常用的局部人工边界有弹性边界、透射边界、粘性边界、粘弹性边界等。弹性边界一般适用于具有很小的能量穿透的远场边界;透射边界程序操作复杂，而且可能引起高频失稳;粘性边界虽然易于实现，但是只能模拟对散射波的吸收，无法实现半无限地基的弹性恢复能力。粘弹性人工边界克服了粘性边界的缺点，在实际工程及科研活动中得到了广泛的应用。

本文应用粘弹性人工边界，考虑土的材料非线性，研究了沥青混凝土路基路面在连续车辆荷载作用下的动力响应，及其路面沉降，并与弹性材料及弹性边界条件进行了对比分析。研究表明，粘弹性人工边界能够很好的实现路基路面动力特性及路面沉降分析，并且具有较高的精度。

1 粘弹性人工边界

粘弹性模型是由牛顿体和弹性体(粘性模型)并联或串联而成。人工边界就是在人为截断的地下边界上，等效建立连续分布的弹性模型和粘性模型并联而成的弹簧—阻尼(Spring-damper)系统，二维平面状态下的人工边界弹簧—阻尼系统如图1所示。

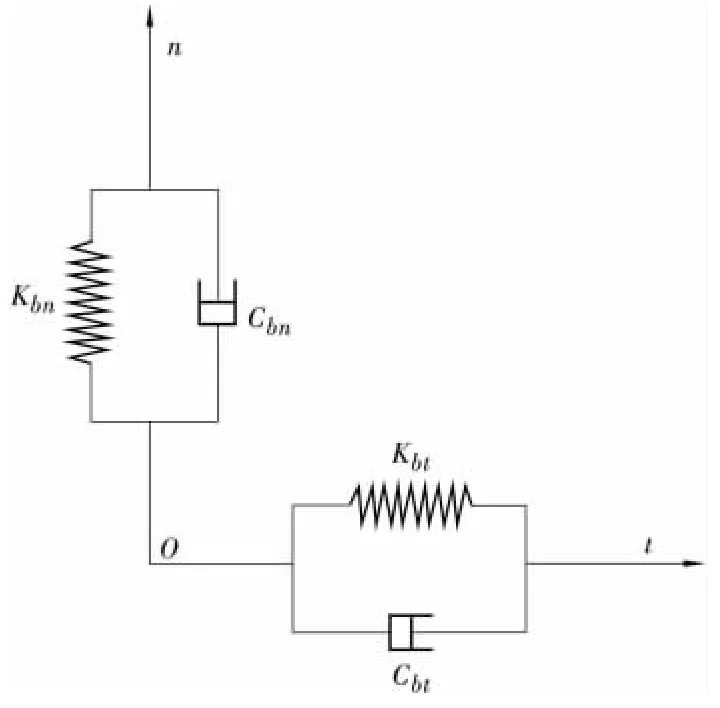
图1 切向和法向的弹簧阻尼系统

其中弹簧—阻尼系统的刚度与阻尼系数由式(1)、式(2)计算可得［2，3］。

式中:Kbt、Kbn分别为系统弹簧元件的切向和法向刚度;Cbt、Cbn为系统阻尼元件的切向和法向阻尼系数;G为截断边界介质的剪切模量;R为人工边界到散射波源的距离;ρ为介质的质量密度;cs、cp分别为切向人工边界的S波速和法向人工边界的P波速;αt、αn分别为人工边界切向和法向刚度修正系数，其取值多由计算结果统计得出，一般取值如表1所示。

表1 粘弹性动力人工边界修正系数αt、αn取值［4］

2 屈服准则及流动法则

Drucker-Prager(D-P)准则是岩石力学中常用的屈服准则，在近30a中得到了广泛的应用。D-P准则是在Mises屈服准则的基础上，考虑了平均应力σm的作用，σm的表达式如式(3)所示。与Mohr-Coulomb(M-C)准则相比，D-P准则能够反映岩石材料在静水压力和高围压作用下的屈服破坏现象。

当 i=j时，δij=1;当 i≠j时，δij=0。I1为应力张量第一不变量。

对于平面应变问题［5］:

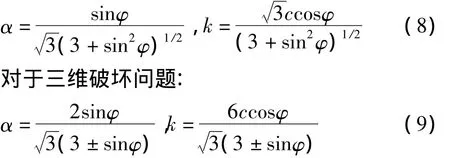
当土为受拉破坏时取“+”，为受压破坏时取“－”。

对应于线性D—P屈服准则，线性流动法则的塑形势函数表达式为:

其中dλ为一非负比例系数;ε代表应变。

3 数值模拟

本文基于ANSYS软件，分别考虑了弹性边界、粘弹性人工边界两种边界条件。土基材料考虑了土的非线性，应用线性D-P屈服模型及流动准则。路基路面部分材料未达到塑形，采用弹性材料进行分析。

3.1 材料选取

考虑5种结构层材料进行分析。在正常车辆荷载作用下，沥青混凝土、密级配碎石和级配碎石很难达到塑形状态，对路面沉降影响很小，因此仅考虑其弹性性能。土基材料分为选取弹性及弹塑性两种，对每种情况下路基路面的动力响应及路面沉降进行对比分析。主要材料参数如表2所示。

表2 结构层材料参数［6］

3.2 模型简介

在ANSYS中，粘弹性人工边界常采用COMBIN14单元类型，需要定义单元的弹性参数与阻尼系数。COMBIN14单元由弹性元件和粘性元件并联的弹簧－阻尼系统，比较符合人工边界条件。COMBIN14单元几何结构示意图如图2所示。本模型中仅采用法向弹簧—阻尼单元。

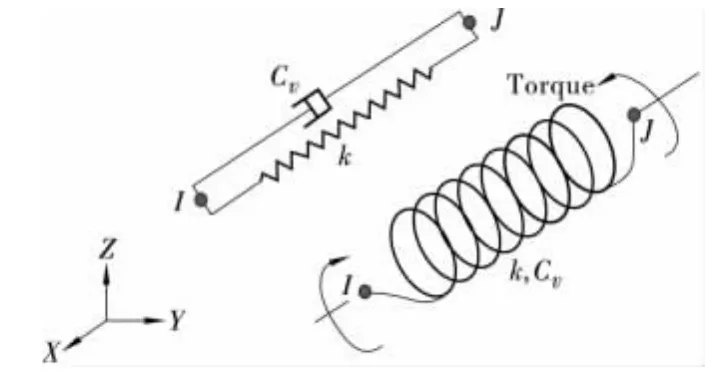
图2 COMBIN14单元结构示意图

模型中路基采用三级公路规定标准，路基宽度为7.50m，路基边坡坡度为1∶1。考虑双向车辆通过截面分析，即结构、荷载对称，数值模拟时采用一半模型进行分析。土基竖向边界与边坡底脚的距离为14m，结构层分布从上往下的厚度依次是12cm、20cm、35cm、8m及7m，以最大程度的接近半无限域，以方便对比。

荷载采用普通车辆荷载计算，模型中用距离1.5m(车辆荷载轮胎中心轴线距离)的两个集中力(分别施加到4、6号节点上，4号节点靠近路面中心轴线)来模拟两个车轮对路面的作用荷载P。设轮胎与路面的作用时间为T=0.4s，荷载大小随时间成1/2正弦函数分布，车轮荷载等效函数如式(12)所示。采用5个周期进行分析，一个周期(4s)内荷载随时间变化曲线如图3所示。阻尼采用Rayleigh阻尼，质量和刚度阻尼系数分别为 0.94、0.026，粘弹性人工边界模型见图4所示。

图3 一个周期内车辆荷载曲线

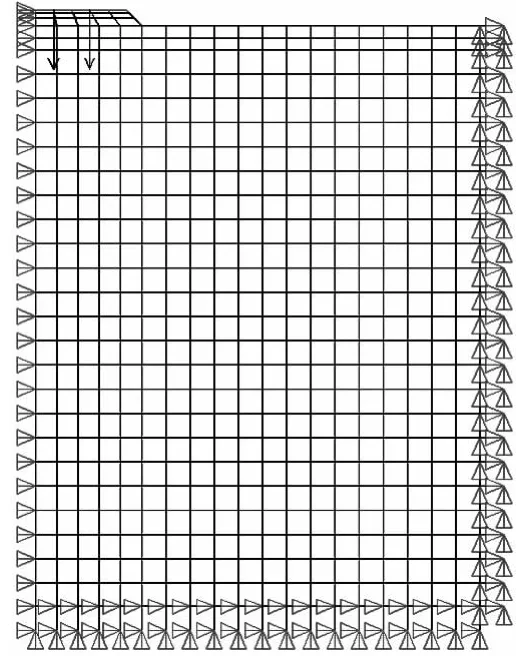
图4 粘弹性人工边界模型

3.3 结果分析

通过模拟计算，分别得出了弹性材料—弹性边界(弹性—弹性)、塑形材料—弹性边界(塑性—弹性)及塑形材料—粘弹性边界(塑形—粘弹性)3种情形在20s内5次车辆荷载作用下的的动力响应结果。如图5和6所示，分别是两个轮胎中心线处节点4和6的位移时程曲线。图中3条曲线从上往下依次对应弹性—弹性、塑性—弹性及塑形—粘弹性条件。

图5 4号节点位移时程曲线

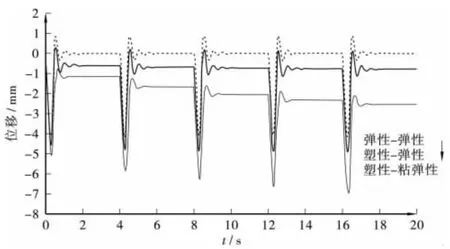
图6 6号节点位移时程曲线

从图中可以看出，边界或材料不同对结构响应均有很大的影响。由于阻尼相同，导致弹性—弹性及塑形—弹性条件下的两条位移曲线震荡时间基本相同。而塑形—粘弹性模型由于在人工边界处存在弹簧—阻尼系统，增加了对能量的吸收，故震荡时间较短。同样，通过位移震荡幅值也可以清晰的看出二者对能量吸收及反射的不同。通过弹性和粘性边界对比发现，模型计算区域的选择对弹性边界的计算结果影响很大。

另外，在连续车辆荷载作用下，局部土基达到塑形阶段，产生不可恢复变形，即沉降。随着荷载作用次数的增加，沉降逐渐趋于稳定。塑性－粘弹性条件下，车轮中线轴线处4、6号节点在5个周期内的沉降值分别为2.62mm、2.54mm，且要经过多次荷载后才能趋于稳定。而在塑形—弹性条件下，两个位置的沉降分别为0.82mm、0.76mm，两次车辆荷载作用后，沉降就趋于稳定，所需荷载次数比塑性—粘弹性条件下要少很多。可见，地基边界的选取对动力响应及路面沉降均有很大的影响。

4 数值模拟

通过对弹性材料—弹性边界条件、塑形材料—弹性边界条件及塑形材料—粘弹性边界条件3种情况进行数值模拟，对比分析了连续车辆荷载作用下3种不同模型的动力响应及路面沉降。研究发现:对于含地基结构的动力响应分析，弹性边界结果的正确性对计算区域的选取有很大的依赖性，而粘弹性边界对计算区域的依赖性较小;对于路面沉降分析，粘弹性边界模型的沉降需要多次车辆荷载作用才能趋于稳定，比较符合实际情形。

［1］廖振鹏.工程波动理论导论(第二版)［M］.北京:科学出版社，2002.

［2］谷 音，刘晶波，杜义欣.三维一致粘弹性人工边界及等效粘弹性边界单元［J］.工程力学，2007，24(12):31－37.

［3］刘晶波，谷 音，杜义欣.一致粘弹性人工边界及粘弹性边界单元［J］.岩土工程学报，2006，28(9):1070－1075.

［4］宋贞霞，丁海平.粘弹性人工边界在大型程序中的应用［J］.防灾减灾工程学报，2007，27(S):43－46.

［5］屈智炯，刘恩龙.土的塑性力学(第二版)［M］.北京:科学出版社，2011.

［6］邓学钧.路基路面工程(第三版)［M］.北京:人民交通出版社，2009.