倒尺尺架技术在建筑物沉降观测的应用研究
张云端,陈燕飞
(洛阳市规划建筑设计研究院有限公司,河南洛阳 471000)
1 引言
建筑物施工前期,周边基坑开挖留下施工区尚未填平或施工区周边地形条件限制,会遇到沉降观测点埋设位置较高,水准仪视线高达不到观测点的高度,无法进行沉降观测的情况,传统的几何水准法难以实施。若采用设置观测墩、观测台,缺点是成本高、作业时间延长,对于建筑物较高的观测点,作业较难实现;传统倒尺观测方法,作业过程中水准标尺垂直状态受作业人员判断,影响观测精度。目前,建筑物沉降观测的研究多侧重于对监测数据的分析研究;水准测量精度分析;倒尺观测读数研究等,缺少针对观测本身提高观测精度的研究,为此本文提出采用倒尺尺架技术进行特殊情况下的沉降观测,可以提高作业速度,保证沉降观测精度,并通过实践验证,方便实用,精度完全可以达到规范要求。
2 倒尺尺架制作及工作原理
2.1 倒尺尺架制作
尺架主要部件包括卡尺部分(右盘)、挂点部分(左盘)、中间部分(双向连接板)。右盘中心处设有高强度磁铁,磁铁镶嵌在主板上且底面与主板底面在同一平面上,确保水准尺底端面与观测点在一个平面上。倒尺尺架材料采用膨胀系数较小的合金钢制作。由于尺架加工要求精度很高,因此采用钢板的平整度要求也很高。尺架主板与双向连接板宽度尺寸小于精密水准标尺底端两个凸点间距,确保水准标尺与尺架较好接合,如图1~图3所示。卡尺部分与水准尺进行连接部位采用强磁性磁铁,可以使标尺底端面与主板贴紧,作业过程中,不产生变形或者变形微小,确保高程传递精度。

图1 倒尺尺架正视图

图2 倒尺尺架侧视图

图3 倒尺尺架与标尺底端套合图
2.2 工作原理
尺架使用时,将水准标尺底端与尺架套合在一起,水准标尺底部落在尺架右盘的触点上,将水准标尺和尺架整个通过左盘触点放到沉降观测点(或沉降钩)上,通过倒置水准器判断标尺竖直后进行观测。
双线连接板可以通过固定螺丝旋进或旋退左右移动,可以根据不同尺寸的水准标尺进行调节。
倒尺水准测量,立尺方向与高程系统反向,所以应在倒尺读数前加上负号,这样高差计算与正尺测量一致,即高差等于后视减前视。主要有以下4种情况:
(1)后视立正尺,前视立倒尺。
高差为:h=a-(-b)
(2)后视立倒尺,前视立正尺。
高差为:h=(-a)-b
(3)沿地面前视、后视均立倒尺,如图4所示。
高差为:h=(-a)-(-b)+△L=(b-a)+△L

式中:LA、LB分别为A尺和B尺的长度,△L通过偶数站自动消除,此时△h=∑(b-a)

图4 地面转站倒尺观测示意图
(4)沿沉降点前视、后视均立倒尺,如图5所示。
其中:h=(-a)-(-b)=(b)-(a)

图5 建筑物沉降点倒尺观测示意图
3 倒尺尺架进行水准测量的读数改正
3.1 倒尺尺架读数改正
倒尺精密水准测量必须对读数改正后,才能使用上面的公式。因为普通水准仪在标尺上的读数是水平视线到标尺理论零点的距离,而精密水准仪由于测微尺的作用,使正尺的读数与这个距离相差一个常数K(如N3,K=0.5 cm),倒尺就不具备以上规律,所以应该按照一定的规律改正,否则会导致严重的错误。
(1)倒尺尺架读数改正规律
如图6所示:当△1≤0.5 cm时,转动测微轮视线上移,测微尺示数减小,与y重合时测微尺示数减小△1,这时测微尺示数减小到e=(0.50-△1),则:
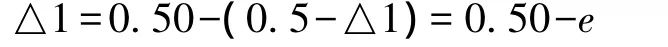
这时实际读数为:

当△2≤0.5 cm时,转动测微轮视线下移,测微尺示数增大,与x重合时测微尺示数增大△2,这是测微尺示数增大到e=(0.50+△2)则:
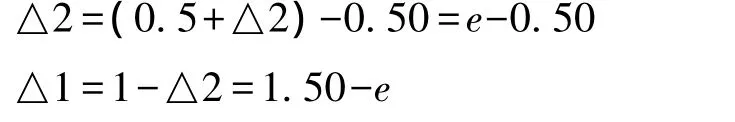
这时的实际读数为:

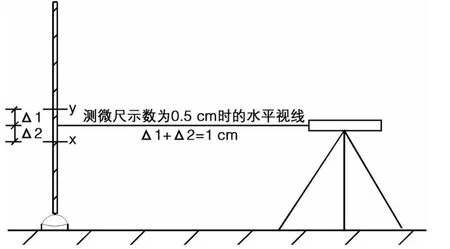
图6 测微尺示数为0.5 cm观测示意图
3.2 读数改正规则总结
依据实际作业:总结以下改正规则:
改正规则一:0.5 cm减去重合时测微尺读数与标尺分划值求代数和,即得到改正后的正确读数。例如按照常规方法读得两倒尺读数为-101.555、-053.420,改正后分别为-100.945、-053.080。
为了防止+0.50 cm造成测量成果的错误,有必要使倒尺测量具有 -0.50 cm这一常数,在高差计算中正负抵消,所以给式(1)、式(2)的两边同时减去0.5 cm,则得:
与 y 分划重合时:y+△1-0.50=y-e
与 x 分划重合时:y+△1-0.50=x-e
改正规则二:重合时标尺分划值减去测微尺示数所得的差,就是改正后的正确读数。例如按照常规方法读得两倒尺读数为-101.555、-053.420,改正后分别为-100.445、-052.580[1]。
由此可见,在精密水准测量中存在±0.50 cm两常数,但无论前后视如何立尺,改正后高差计算均会自动抵消,但单向观测应注意。实践证明,规则二改正可提高计算速度,建议在实际工作中使用规则二对观测数据进行改正。表1为改正规则应用高差计算结果。其中采用仪器型号为WildN3。

改正规则应用高差计算表表1
4 尺架常数的测定
由于尺架在制作过程中会因微小的误差使标尺底部与卡尺部分的平面不能完全重合,这样在观测的过程中就会形成由尺架制作不精密而造成的误差,我们把这个误差值称为尺架常数,因此在尺架制作完成后,均应对尺架反复试验,测定其常数,对观测结果进行改正,得到正确的观测数据。若尺架制作严密,理论上尺架常数可以忽略不计。
取固定后视方向(正尺),选择正、倒尺均能进行观测的若干个沉降观测点(本文取两个点为例),对它们多次观测取平均值,得到尺架常数。首先前视用正尺分别观测后视与前视观测点的高差,多次观测取平均数,然后前视使用倒尺再一次测后视与前视观测点的高差,取平均数。则正、倒尺的高差之差为尺架常数。
本次观测以1 m标尺(9589)和2 m标尺(23776)为例测定尺架常数。数据汇总如表2所示:

尺架常数计算表 表2
由表2可以看出:1 m标尺(9589)和2 m标尺(23776)所测得的结果分别为 -0.26 mm、+0.29 mm,说明尺架制作精度较高,观测结果可视为观测误差,则尺架常数可忽略不计。
实践证明:在观测的过程中,对尺架卸掉再重新安装,同一点的观测高差值不变。如表3所示:
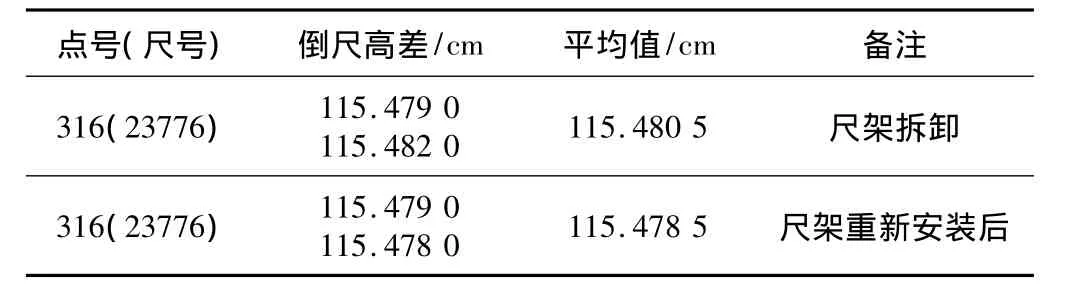
尺架拆卸高差计算表 表3
5 结语
采用倒尺尺架进行建筑物沉降观测,可以简化工作,提高工作效率,实用性很强,但应对读数行改正。倒尺尺架在使用过程中能满足作业要求,但部件亟待进一步的研究完善,使其外观更加美观,适用性更强。本文以水准仪WILD N3为例进行描述,通过对其他型号水准仪实验,改正规则适用于其他型号的水准仪,规则只考虑数值,不考虑负号,改正后再加上负号即可。在现场观测中可以直接使用规则二对读数进行改正。整数位是标尺分划值减1,小数位是1 000减去测微尺示数,这样提高现场计算速度。
[1]田养权.倒尺精密水准测量[J].浙江测绘,1991(4):1~4.
[2]吕文广,徐明.提高建筑物沉降观测精度的方法[J].测绘信息与工程,2007,32(3):44 ~45.
[3]朱旭.对精密水准测量中水准标尺倒立时的读数化算问题初探[J].煤炭技术,2008,27(10):162~163.
[4]黎明星.建筑物主体沉降观测非常规方法探讨[J].建材发展导向,2012(10):23.
[5]黄张裕,于涛,袁峥.两种特殊情况下的建筑物沉降观测方法[J].测绘工程,2006,15(5):57~60.
[6]赵德珍,李朋.浅谈高程控制测量中倒尺法的应用[J].山东水利,2011(5):42.
[7]陈学彬,李旭.倒尺法在高程传递中的应用[J].城市勘测,2011,2(1):148 ~149.
——黄咏梅小说论

