从一道变质量问题区分牛顿定律与动量定理解题的不同
史 博 陶宗明 张 辉 麻晓敏
1 引言
在动力学中常常会遇到变质量问题,例如,一辆装煤的车以水平速率v从煤斗下经过,每秒落入车厢的煤质量为Δm,如果车厢速率保持不变,应用多大的力牵引车厢?(忽略车厢与钢轨间的摩擦)
此题可以落下的煤为研究对象,运用质点的动量定理;也可以煤和车为系统,运用系统的动量定理.当以煤和车系统为研究对象时,是否也可以运用动量定理的微分形式即牛顿第二定律呢?即
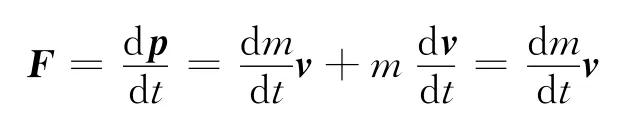
(车的速率保持不变)
由此得到的结果与运用系统的动量定理得到的结果是一致的,但这类变质量问题是否可以应用这一形式的牛顿定律呢?由此想到,低速条件下对于运动速度不变而质量变化的物体,牛顿定律是否可以写成如下的形式呢?
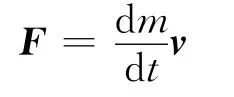
2 讨论
2.1 这一形式的牛顿定律是不对的
对于质点的牛顿定律而言,在低速情况下质点的质量是不变的,不能因为物体的合并、分离就把它看成变质量问题;而对于质点系的牛顿定律即质心运动定理,物体的合并和分离要考虑质心的运动情况,而不是部分的运动情况.
2.2 引言中的问题纯属巧合
引言中给出的例题中,下落的煤落在车上前水平方向的速率为零,但如果下落的煤在水平方向上有初始速率v1(设v1<v),这一形式的牛顿定律还能解决此问题吗?
讨论如下,此时可以在水平方向上运用质点或系统的动量定理.如运用系统的动量定理,设Δt时间内落下了质量为Δm的煤,车和落下的煤这个系统水平方向的初始动量为m v+Δm v1,以共同速率v运动时动量为(m+Δm)v,动量增量为Δm(v-v1),则FΔt=Δm(v-v1),得到
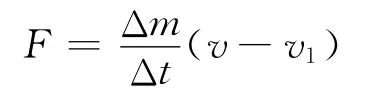
2.3 关于其他变质量问题
例如,质量为m的均匀软链条,长为L,上端悬挂,下端刚和地面接触,由于悬点松脱使链条自由下落,试求链条落到地面上的长度为l时,对地面的作用力.

图1
如图1所示,落在地面上的链条质量在不断变化,此类问题属于变质量问题,同样可以通过质点或质点系的动量定理解决.
方法1:在竖直方向上进行分析,选择向下为正方向.当已落下的链条长度为l时,设其对地面的作用力设为N1,则
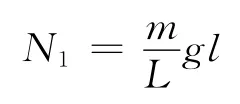
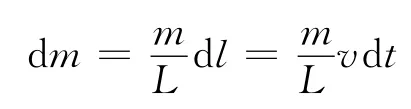
在竖直方向上运用质点的动量定理
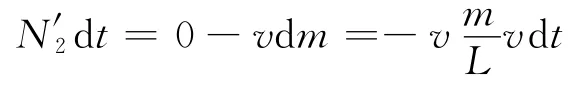
得到微元受到地面的作用力
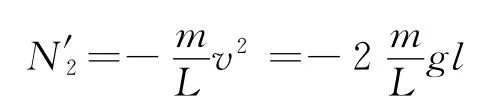
而dm对地面的作用力

地面受到的总的作用力
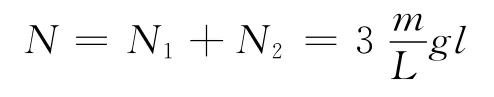
方法2:与方法1相同首先得到
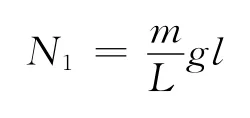
以落在地上的链条和其后dt时间内落下的链条系统为研究对象,系统初动量
p0=0+vdm
末动量 p=0
其中
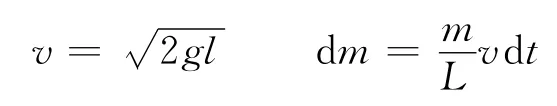
设系统受到地面的冲力为N′2,在竖直方向上运用系统的动量定理,则
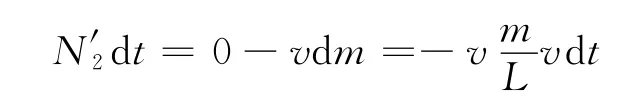
得到系统受到地面的冲力

而系统对地面的作用力
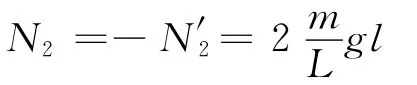
地面受到的总的作用力
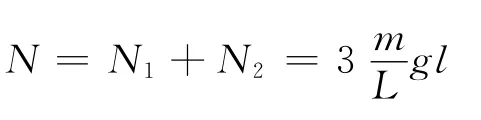
通过质点或质点系的动量定理都可以解决此类问题,但却不能直接在竖直方向上运用牛顿第二定律F=这一形式.
3 结束语
引言中的问题很容易形成误导,使人认为对于速度不变而质量改变的系统,运用F=很简单就可以解决,但此问题可以运用F=得到正确结果只是巧合而已,对其他变质量问题却不适用.通过讨论给出了牛顿定律与动量定理解题的不同,同时可得到这样的启示,对问题的研究、思考要深入,不能只看表面,也不能只跟着感觉走.
1 张三慧.大学基础物理学(上).北京:清华大学出版社,2010 .69 ~72
2 陶宗明.大学物理(第1版).上海:上海交通大学出版社,2000 .42 ~45
3 屈志红.关于动量定理的应用.锦州师范学院学报,2003 (1):88 ~89

