改进的PSO 在并联机构模糊PID 控制器中的应用*

刘伟锐，赵恒华

(辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001)

0 引言

同传统的串联机构相比，并联机构具有刚度大、承载能力强、精度高和结构紧凑等特点，适合于工作空间小、负载强度大的应用场所，在机床加工、飞机制造、医疗等方面也有广泛的应用［1］。随着计算机技术的发展，人们利用人工智能的方法将数学模型和操作经验存入计算机建立控制系统模型，以便对整个机械系统进行控制。但在并联机构控制系统中，存在不确定性、系统的非线性以及外界的干扰等因素，所以建立精确的控制系统模型是非常困难的，模糊控制及其与其他控制理论结合能够很好的解决此类问题并受到广大研究者的青睐。模糊控制是利用模糊数学的基本理论和方法，把规则的条件和操作用模糊集表示，并把这些模糊控制规则及有关信息作为知识存入计算机知识库中，然后根据控制系统的实际响应情况，运用模糊推理，即可自动实现对PID 参数的最佳调整，这就是模糊PID 的控制。本文分析了并联机构的控制策略以及传统PID 控制的优缺点，设计了一种模糊PID 控制器，并加入一种基于解空间划分的改进粒子群算法，优化模糊控制器的量化因子和比例因子，利用模糊PID 控制器对3-TPT 并联机构进行设计和仿真，得到较好的控制效果。

1 并联机构简介

图1 为3-TPT 并联机构示意图，它是由定平台、动平台、平行机构、连杆和驱动杆等几部分组成。动平台与定平台均为正三角形，每根驱动杆和平行机构分别用虎克铰与动平台和定平台连接，伺服电机驱动三根驱动杆的伸缩，通过改变各驱动杆的长度，可以调整动平台的位置。三根驱动杆承受外力，由从动平台和支撑杆组成的平行机构限制三个转动自由度，承受外力矩［2］。

图1 3-TPT 并联机构

自由度用KutzbachGrable 公式计算:

式中:F—自由度;n—总构件数;g—运动副;f i—第i个运动副的相对自由度。在并联机构中，总构件数n=8，运动副g=9，每个虎克铰具有2 个转动自由度每个移动副具有1 个自由度，所以15 ，代入(1)式，F=3，所以3-TPT 并联机构自由度为3。

2 粒子群优化算法

2.1 PSO 算法简介

粒子群优化算法是一种利用群体协作达到目的的全局智能优化算法。PSO 是模仿鸟类群体捕食的过程，在PSO 算法中每个粒子根据全体粒子和自身的搜索经验朝着最优解方向“飞行”［3］。PSO 首先初始化一群粒子N，然后通过迭代过程找到最优解，在每一次迭代中，粒子通过跟踪个体最优位置极值和全局最优位置极值更新自己的速度和位置。更新公式如下:

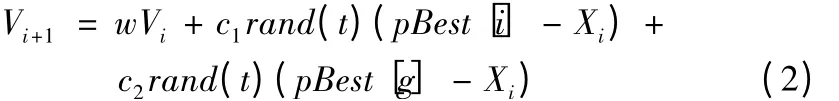
其中，Xi+1=Xi+Vi+1;Vi:第i个粒子进化速度;Xi:第i个粒子位置;pBest［i］:第i个粒子经历的“最好”位置［3］;g:表示群体中“最好”粒子的位置;w:惯性权重;c1，c2:加速因子;rand(t):随机函数，产生［0 1］的随机数值。

2.2 基于解空间划分的PSO 改进算法

解空间是源于线性代数中的一个名词，其定义如下:如果ξ1，ξ2，... ξn是一般齐次线性方程组的n个解，则它们的任一线性组合c1ξ1+c2ξ2+… +cnξn也是该齐次线性方程组的解向量，将所有解集合构成一个向量空间，就叫做解空间。对解空间进行划分可以精确和细化PSO 算法。其中最关键的就是测定最值区间p，p稳定则其他区间也基本稳定［4-5］。解空间的划分方法如下:

(1)初始化粒子种群属性，如等间距分布和速度等差值分布;

(2)记录每个粒子的测试值，统计各粒子所有解，按被初始化属性对所有粒子进行排序，找出各个最值区间和极值区间，计算概率p;

(3)如果概率p值稳定，则输出p值;否则扩大粒子群规模一倍，返回(1)。

概率p的测定方法:设n次测试后，获得的概率(p1，…，pn)，当i≥n/2 且满足时，认为概率p较为稳定，其中，当β≤0.001时即可满足实验要求。

2.3 PSO 算法在模糊PID 中的应用

模糊PID 控制中的量化因子E、EC和比例因子KP、KI、KD均会影响整体控制效果。随着随机因素和不确定因子的增加，单凭人工经验调节量化因子和比例因子显然是比较困难的，不仅带有盲目性，而且很难得到最优解，所以无法得到令人满意的控制结果。本文通过Matlab 将改进的PSO 算法以计算机语言形式编入到m文件中，然后利用Sim 函数得到的目标函数对上述5 个参数进行优化。首先将各参数的初始值输入到参数矩阵X中，然后利用Simulink 建立仿真系统框图，以mdl 文件格式保存;利用仿真函数Sim 编写目标函数程序，最后利用先前编辑的m文件对此目标函数进行优化。

3 模糊PID 控制器

模糊控制是模糊集合理论中的一个重要方面，是以模糊集合化、模糊语言变量和模糊逻辑推理为基础的一种计算机数字控制。模糊控制直接采用语言型控制规则，在设计中不需要建立被控制对象的精确数学模型，利用具有模糊性的语言控制规则来描述控制过程，因而使得控制机理和策略易于接受与理解，设计简单，便于应用。基于模糊原理的模糊系统具有万能逼近的特点［6］。

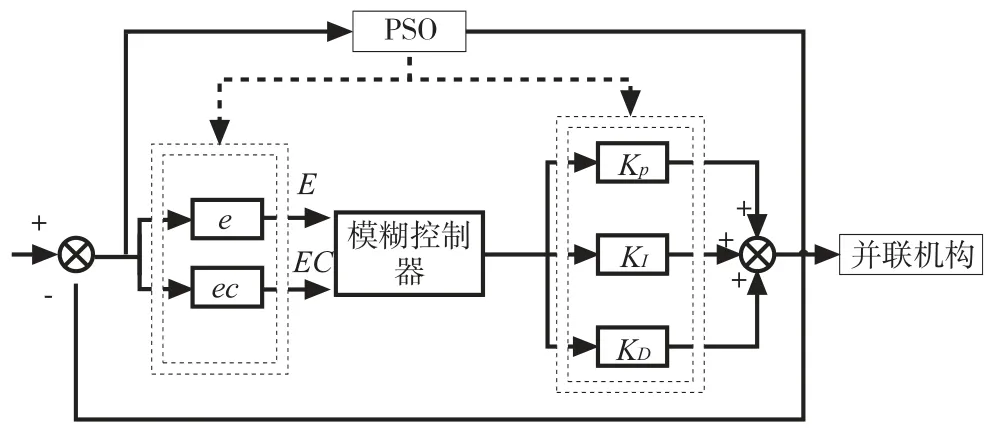
图2 模糊PID 控制结构

模糊PID 控制器的结构为二输入三输出，输入量为偏差绝对值e和偏差变化ec，输出为KP，KI，KD，如图2 所示。利用粒子群算法优化偏差量化因子E、偏差变化量化因子EC和比例因子KP，KI，KD，然后通过模糊PID 控制器对其值进行模糊运算，求出PID 的参数修正值，以此达到PID 控制器的自整定功能［7］。实现模糊控制的实现需要经过模糊化，建立模糊算法和去模糊化三个关键步骤。

(1)模糊化

模糊控制器的输入变量e与ec都是确定数值，进行模糊推理前应模糊化处理。取ec的论域为［-3，-2，-1，0，1，2，3］，语言变量有7 个都为{负大，负中，负小，零，正小，正中，正大}英文缩写{NB，NM，NS，0，PS，PM，PB}，一般取NB为Z 型隶属度函数，PB为S型隶属度函数，其余取三角形隶属度函数。ec的隶属度函数如图3。

(2)模糊控制算法

一般的模糊规则为:If (e is NB)and (ec is NB)then (Kp is PB)(Ki is NB)(Kd is NS)，控制器中共49条规则。图4 为模糊PID 控制曲面图。在不同的e和ec下，对参数修正值KP，KI，KD的自整定规律如下:

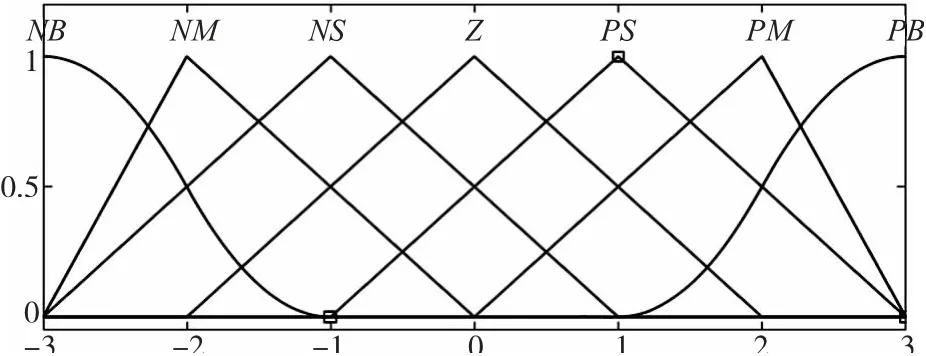
图3 ec 的隶属度函数

1)当e较大时，取较大的KP和较小的KD，同时为了减小超调，通常令KI=0。

2)当e和ec处于中的大小时，取较小的KP，此时的KD值对系统影响较大，KI取值要适当。

3)当e较小时，应使KP、KI取得较大，为了避免出现震荡，要取适当的KD，其原则为:ec较小时，KD取较大;ec较大时，KD取较小值。

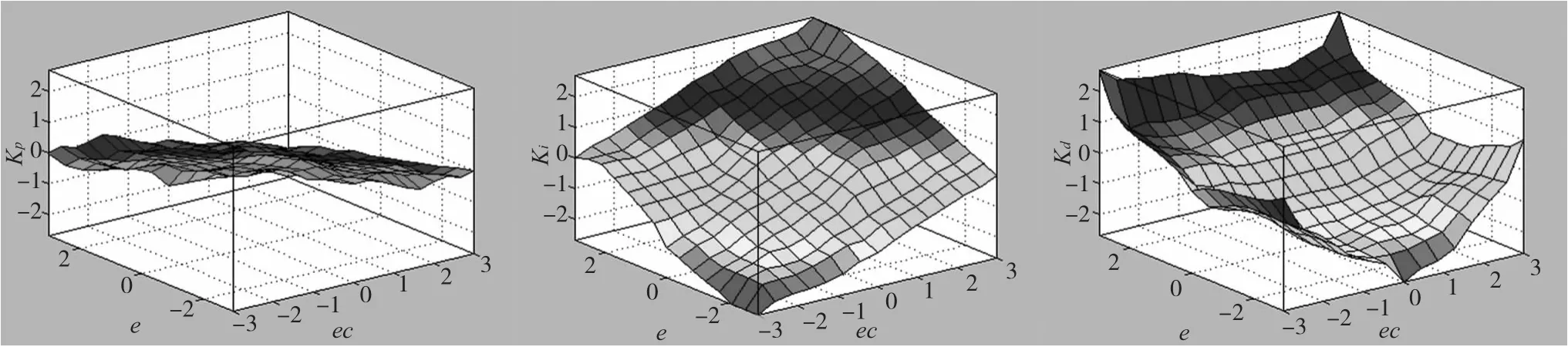
图4 为模糊PID 控制规则曲面图

(3)去模糊化

模糊控制器的输出量是一个模糊集合，它必须转换为非模糊值输出才能用于调节。常见的去模糊法有:最大隶属度法，最大平均值发，加权平均法和重心法。本文选用重心法完成输出量的精确化。

4 仿真

本文利用Simulink 建立控制系统，首先利用Matlab 中的模糊控制箱设计控制规则［8］，然后将其导入到Simulink 中，封装成模糊逻辑控制器，为了缩短仿真时间，加入零阶保持器［9］，如图5 所示;最后建立模糊PID 控制器，如图6 所示。利用SimMechanics 模块建立3-TPT 并联机构的结构模型，与控制器连接起来进行联合仿真。

图5 模糊逻辑控制器

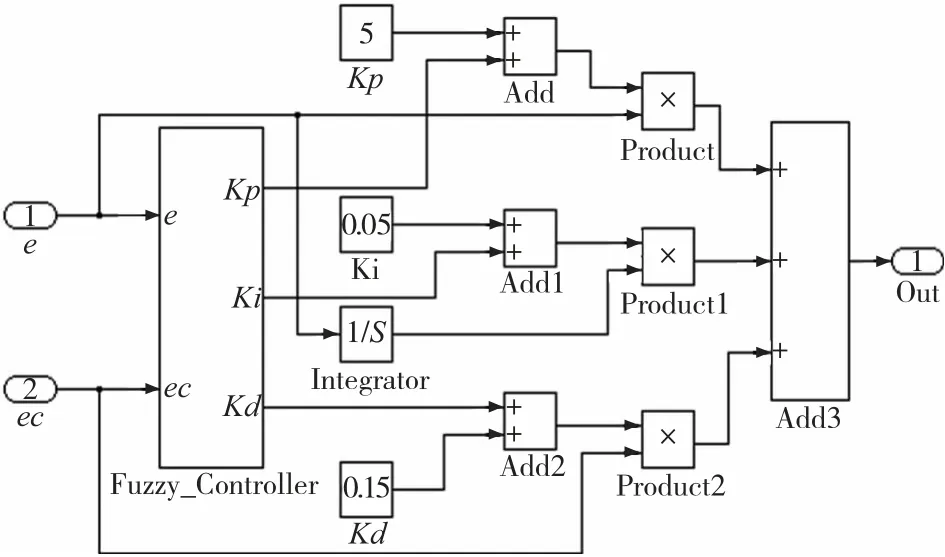
图6 PSO 模糊PID 控制器

算法步骤如下:

(1)确定优化对象。分别对模糊控制器的E、EC、KP、KI、KD五个参数进行寻优。

(2)初始化粒子群参数。规定种群规模200，最大迭代次数为200，加速因子c1 =2，c2 =2，最大速度V=0.2，惯性权重w=0.8。

(3)确定适应度函数。考虑到阶跃响应在过渡过程中的动态特性，本文采用ITAE 指标［10］，即误差绝对值乘时间积分准则这一指标作为适应度。一般采用ITAE 指标的控制系统通常具有平稳、快速和超调小等优点，表达式如下:

(4)利用公式(2)进行迭代运算，同时计算适应度值。比较粒子适应度值和自身最优位置，并替代种群最优位置。最后检查结果是否满足精度要求，否则t=t+1。

设定3-TPT 并联机构中的参数R=600mm，r=200mm，;图7 为改进的PSO 进化曲线，可以看出该算法前期收敛速度很快，后期为搜索最优解收敛速度放慢，此方法有效的解决了局部收敛的问题。模糊PID各参数为:ke= 4，kec= 30，Kp= 5，Ki= 0. 05，Kd=0.15;模糊逻辑控制器中k1 =0.5，k2 =0.1，k3 =0.2。仿真结果如图8 所示。由图8 所示，经PSO 优化的模糊PID 控制与传统模糊PID 控制相比，优势比较明显:上升时间短，超调量小，到达稳态时间短，几乎无系统误差，动态性能较好。

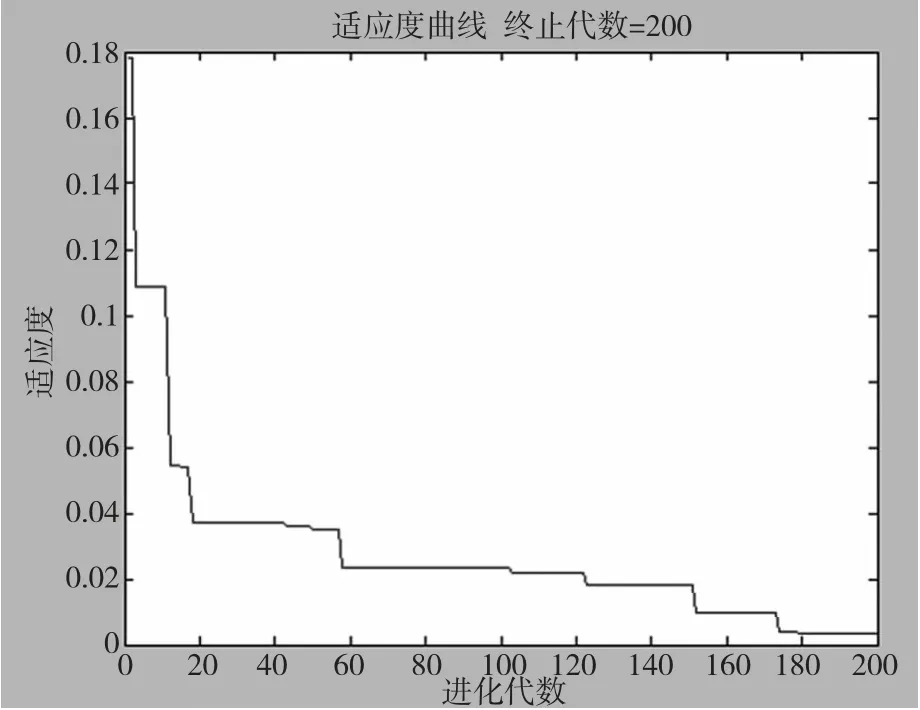
图7 粒子群算法进化曲线

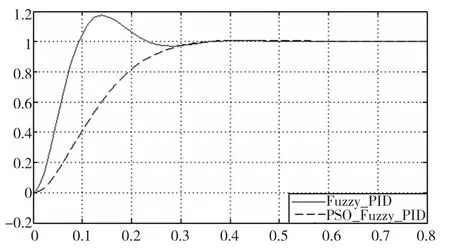
图8 仿真曲线

5 结束语

本文利用了一种基于解空间划分的改进粒子群算法，优化了模糊PID 控制器中的量化因子E、EC 和比例因子KP、KI、KD，并将其应用与3-TPT 并联机构中，实现了精准自适应控制。由仿真结果可知，与传统的模糊PID 控制器相比，它具有调节时间短，无系统误差，稳定性好，鲁棒性强，提高了系统的动态性能，可以取得满意的控制效果。

［1］金云龙. 并联机床的研究现状和发展前景［J］. 企业技术开发，2010，29(6):128 -129.

［2］杨辉，赵恒华，付洪栓. 并联机构虚拟样机的构建与仿真［J］.工程设计学报，2012，19(6):445 -448.

［3］车林仙.4-RUPaR 并联机器人机构及其运动学分析［J］.机械工程学报，2010，46(3):36 -41.

［4］车林仙，何兵，易建，等.对称结构Stewart 机构位置正解的改进粒子群算法［J］.农业机械学报，2008，39(10):159-163.

［5］赵伟，蔡兴盛.基于解空间划分的PSO 改进算法［J］.吉林大学学报(理学版)，2012，50(4):725 -732.

［6］黄麟，荆萃，赵翱东. 基于改进粒子群算法的主动悬架模糊PID 控制研究［J］.煤矿机械，2012，33(10):39 -41.

［7］洪超. 一种用于柔性定位器的三自由度并联机构研究［D］. 南京:南京航空航天大学，2010.

［8］高继良.三平动并联机构传动动力学和双轴同步控制研究［D］.南京:南京理工大学，2012.

［9］文振忠.基于粒子群优化的模糊神经PID 的发电机励磁控制研究［D］.西安:西安电子科技大学，2009.

［10］崔雪兵.基于PSO 的同步发电机模糊PID 励磁控制研究［D］.沈阳:东北大学，2010.