基于多频谱分析的机械故障定位研究*

王 磊，张清华，马春燕，何 俊

(1.太原理工大学 信息工程学院，太原 030024;2.广东石油化工学院 计算机与电子信息学院，广东茂名 525000)

0 引言

工业机械设备检修所测的振动信号一般为时域信号，即描述振动信号随时间变化的情况［1］，基于时域分析的方法广泛应用于机械故障诊断领域，但时域分析提供的信息往往是非常有限的，只能简单的回答机械设备是否发生故障，不知故障发生的具体位置，故一般用作设备的简易诊断。随着科学与技术的发展，各个学科之间的交叉和相融，促进了旋转机械故障诊断技术的快速发展。神经网络［2］、专家系统［3］、模糊逻辑系统、遗传算法、人工免疫、频谱分析等技术在机械故障诊断方面的应用得到了一定的拓展，神经网络是一个非线性动力学系统，能够对信息分布式存储和并行协同处理，由大量的神经元网络构成系统，能够较容易地处理离散或者连续数据，具有很好的泛化能力，但知识的利用和表达单一，不能够很好的解释推理过程，只能简单的描述人类的表面感觉层次［4］。专家系统是一个基于知识的系统，利用人类专家提供的专门知识，模拟人类专家的思维过程，解决对人类专家相当困难的问题，具有启发性、透明性和灵活性，但不能够处理不是明确包含在专家知识领域内的新状况。模糊逻辑系统不仅允许明确信息的输入，也允许模糊信息的输入，能够处理明确和模糊的信息，但对模糊规则的自动提取比较困难。遗传算法由于其自身的进化特性，对所求解的优化问题没有太多的数学要求，能够非常有效地进行概率意义上的全局搜索［5］，但其不容易编码，并且易出现早熟现象。人工免疫技术通过对生物免疫机制的模拟，具有强大的信息处理能力，在参数选优方面具有一定的优势［6］，但其容易陷入局部最优的平衡状态，得不到全局最优解，导致属性的约简结果受损。对于频谱分析技术，所有的信号都是由不同频率的正弦波组成的，频谱分析就是在这些频率的基础上找出它们的正弦波成分及其幅度和相位，在许多情况下基于时间变化的信号看不出什么问题，但经过频谱分析以后，找出了它的频率成分，问题就很好的呈现出来，而一般的频谱分析技术是基于单一的谱进行故障诊断分析，虽然此类故障诊断分析技术有了一定的诊断准确率，但不是很高。因此本文针对各种智能故障诊断技术及其单一频谱分析技术存在的不足，提出基于频谱、倒频谱、功率谱多频谱故障诊断分析算法，并将其应用在旋转机械故障诊断实验中，通过实验验证了此技术的可行性和有效性，较单一频谱分析提高了故障诊断精度。

1 频域谱分析

1.1 频谱分析

频谱分析技术是基于频域的振动信号分析，对信号主要进行“傅里叶变换”，把本来随时间变化的信号表示方式变换为随频率变化的“频谱函数”方式。频谱分析以机械设备内部存在缺陷时所引起的振动频率图与机械设备正常运行时振动频率图的差异作为判断依据，通过频谱分析设备测量出机械设备在这两种状态下的振动数据和相关参数，利用这些参数能够进一步分析设备内部的运行状况，机械设备的频谱分析过程，能够对机械设备的工作状态进行判断和预测［7］。根据机械振动原理，机械系统的振动响应过程中一定包含着频率成分，并有与之对应的同频激振源:一个或多个频率分量幅值增大，一定与激振力的幅值增大相关。频谱分析设备的用途就是识别信号中的频率成分，进一步分析故障诊断的类型。因此，利用频谱分析技术能够基于频域的角度探究机械设备振动响应过程的频率组成成分、强度以及机构变化等，能够为振动故障的识别提供丰富的故障特征信息。

实际应用中基于频谱的分析技术一般是幅度谱的分析，所谓幅度谱分析，就是对设备采样所得的时域信号进行傅里叶变换，求得关于时域信号的频率构成信息，其数学表达式为

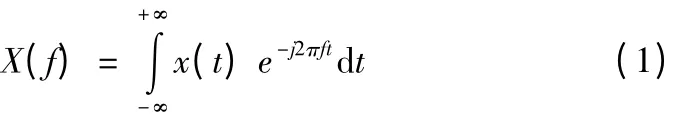
式中x(t)—时域信号(振动速度、加速度、位移等一切以时间t为自变量的函数)。

X(f)—信号的幅度谱，是以频率为自变量的函数。

幅值谱以频率作为自变量，以组成信号各个频率成分作为因变量而构成。在故障诊断分析时，由于摒弃了相位信息，使频谱图的组成更加明朗化，分析更加直观，但正因为失去了相位信息，导致了故障诊断误差相对加大。

1.2 功率谱

功率谱是基于信号能量或功率分布情况的描述，包含自功率谱和互功率谱，其中自功率谱与幅度谱提供的信息量相同，但是在同一条件下，自功率谱较幅度谱更清晰。因此，自功率谱在泵齿轮［8］及感应电动机［9］的故障检测中的应用也得到一定的研究。自功率谱的计算公式如下:

自功率谱估计也分为线性估计法与非线性估计法，线性估计法以快速变换为基础，应用较早，也称为经典谱分析法;非线性估计法是与时域模型相结合的一种新型方法，又被称作现代谱分析法。经典谱估计法是假设数据工作区外的未知数据为零，相当于数据加窗，主要有自相关法和周期图法。自相关法由一定的序列估计出自相关函数，然后再对其傅里叶变换，得到这一序列的功率谱估计;周期图法是把随机序列的若干个观测数据作为一个能量有限的序列，直接计算这一序列的离散傅里叶变换，得到一数据，然后再取其幅值的平方，并除以N，作为研究序列的真实功率谱估计［10］。现代谱估计主要是通过观测数据的参数模型，然后以求参数模型输出功率的方法估计信号功率谱。

经典谱估计方法方差性能不稳、分辨率低、谱图易畸变［11］，但用现代谱功率估计，频率分辨率不会因数据的长短而产生太大变化，因此现代谱功率估计广泛应用于振动信号分析处理［12］，而用现代谱估计时，谱形的质量受模型阶次的影响，当阶次太低时，谱形会过于平滑，反应不出谱峰。当阶次过高时会产生虚假峰值，对诊断的精度造成了一定的影响。

1.3 倒频谱

倒频谱在周期信号的检测时具有较强的辨析能力，它主要利用傅里叶变换将原始信号的周期信号转变成离散型的谐波成分，并且在变换过程中与对数转换相结合以防止振动能量较弱的周期信号被忽略［13］。倒频谱分析是故障诊断中精密诊断的一种有力手段。广泛应用于振源、噪声源识别、故障诊断、去除回波等场合。

倒频谱变换主要有两种分析方法:复倒谱分析和实倒谱分析。复倒谱分析保留了信号的全部信息，能够基于信号的回声检测;实倒谱分析则在变换过程中保留了信号的频谱幅值成分，摒除了相位信息，所以不能对信号进行重建，但是可以利用它来进行重建一个最小相位信号。

倒频谱有多种定义，常见的是功率倒频谱和幅值倒频谱，但一般实际应用中基于幅值倒频谱分析，其公式如下:

倒频谱是频域信号的傅里叶变换，倒频谱的自变量τ 称为倒频率，其单位一般是时间毫秒(ms )，Gx(f)是功率谱函数。

倒频谱是频谱的频谱，它可以分析繁杂频谱上的周期结构，分离和提取出频谱中的周期信号。倒频谱变换在分析时，既不会漏掉边频信号，又能给出非常精确的间距结果，因此倒频谱分析技术在故障诊断中的应用越来越广，由于在对振动信号的提取时，外界的干扰信号比较多，干扰信号和故障的特征信号相同或者相近时，就会严重地影响故障诊断精度。

1.4 多频谱分析算法

频谱、功率谱、倒频谱等单频谱故障诊断分析技术虽然具有各自的优点，在各个领域也有了一定的应用，但由于自身存在的缺陷和不足，仅仅单靠一种或者两种频谱技术对故障分析时，可以得到相应的诊断结果，但故障诊断准确率较低，甚至当数据干扰较大时，出现不能够进行相应故障分析的现象。因此本文利用频谱、功率谱、倒频谱各种技术的优点，将它们融合在一起分析，提出多频谱分析算法，分析原理如图1 所示。

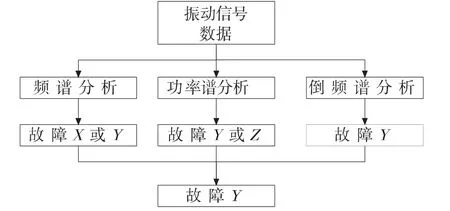
图1 多频谱分析算法流程图

由图1 可以看出，当分别利用频谱、功率谱、倒频谱技术对同一组振动信号数据单一分析时，可能会出现一种或者两种不同的故障分析结果，即通过频谱分析后的结果可能为故障X或者故障Y，经功率谱分析后的结果可能为故障Y或者故障Z，倒频谱分析后的结果为故障Y，由于它们的诊断结果有相同的交集，即都出现诊断结果为故障Y，因此得出诊断结果为故障Y。

本文就是基于排除分析法的原理，提出多频谱分析算法，当出现干扰故障的时候，采用诊断结果两两相结合，排除干扰的诊断结论，最终得出正确的诊断结果。

2 机械故障定位实验及分析

2.1 机械故障定位实验

本文使用北京伊麦特科技有限公司生产的EMT390 数据采集器对组合式旋转机械试验装置进行各种故障轴的加速度振动信号采样，EMT390 数据采集器通过一个传感器采样数据，我们将传感器探头放在距轴6.5 厘米处，电动机转速1500r/min，采样频率为1000Hz，采样点数1024 点，每种故障取50 组数据，然后利用多频谱分析技术对各种数据进行分析研究，实验装置如图2 所示。

图2 组合式旋转机械实验装置

组合式旋转机械试验装置所需仪器为机架、低噪声轴流式通风机、变频调速三项异步电动机、减速机和轴(正常轴、不对中轴、裂轴、弯轴和偏心轴)。

我们采用四种故障数据和一组正常数据进行频域分析实验，各类频谱方法对故障的诊断结果如表1 所示。

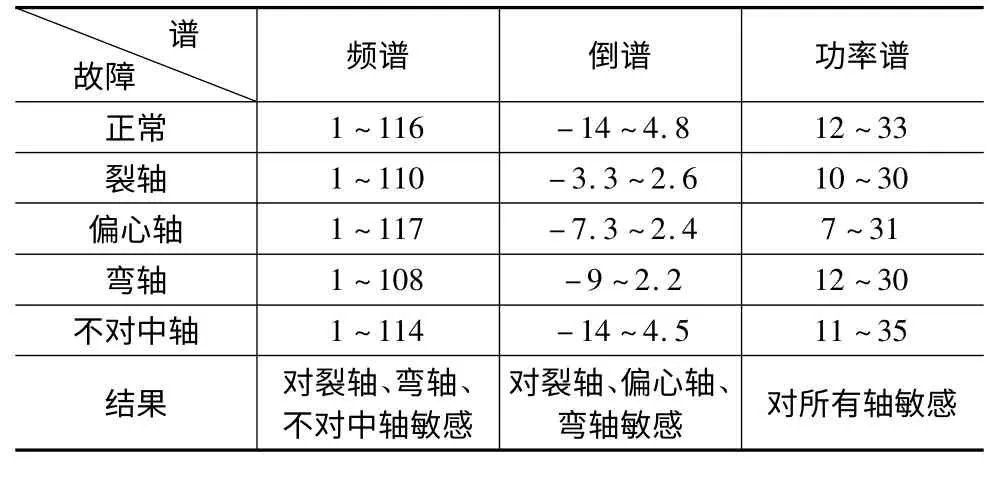
表1故障轴的各种频谱图的振幅分析

由表1 可以看出单一频谱分析结果并不是对所有的故障敏感，容易产生故障诊断误差，而多频谱故障诊断分析算法能够排除干扰的实验数据，得出正确的故障诊断结果，下面基于多频谱故障诊断分析算法对加速度振动信号采样数据分析，来判断此算法的可行性。

2.2 机械故障定位实验结论分析

现在分别任选一组裂轴和正常轴的加速度振动信号采样数据，并进行基于频谱、倒谱、功率谱的多频谱分析，其谱图如图3～图8 所示。

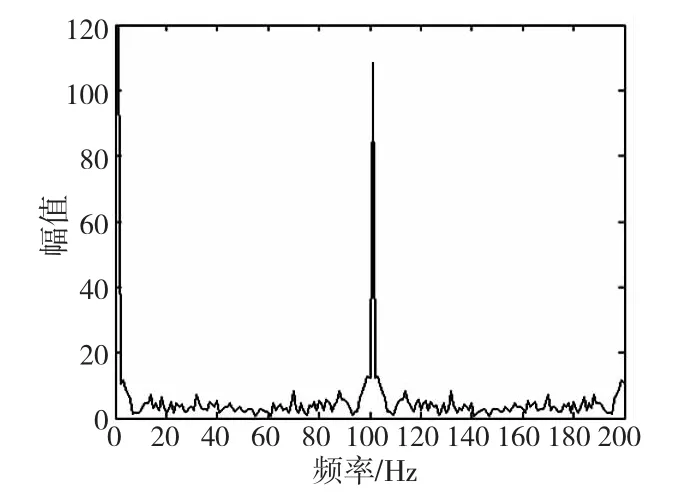
图3 裂轴测试数据频谱图

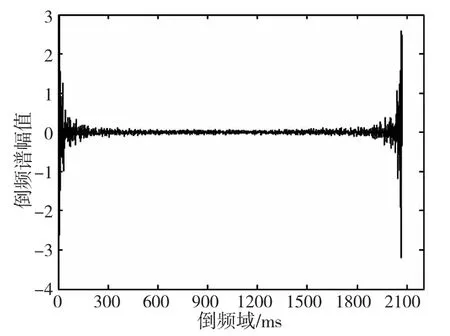
图4 裂轴测试数据倒谱图

图5 裂轴测试数据功率谱图

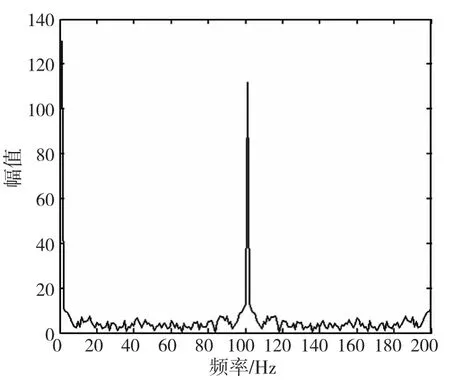
图6 正常轴测试数据频谱图

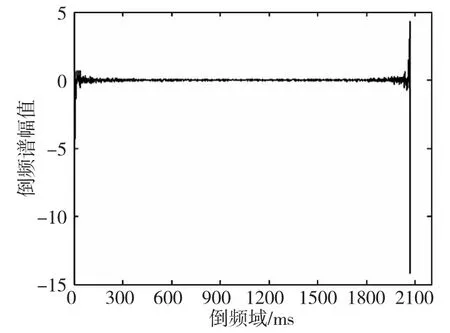
图7 正常轴测试数据倒谱图

图8 正常轴测试数据功率谱图

由以上各图可以看出在开始时间的振幅波度较大，此主要是由数据采集初振动信号不稳定造成，故此阶段的振幅异常不做考虑。由图3 得出频谱图中振动信号的振幅范围为1～109.5，故障频率集中在中频段，特征频率为100Hz，比对表1 可得此故障为裂轴，但也有属于弯轴的可能性，由图4 可得倒谱图中振动信号的振幅范围为-3.3～2.5，比对表1 得出此故障为轴的裂纹，排除了弯轴的可能性，正确诊断出故障类型。为了验证此方法对正常和故障的区分度，采样了一组正常轴的加速度振动信号，此振动信号的谱图如图6、图7 和图8 所示。由图7 可得振动信号的振幅范围为-14～4.6，对比表1，此信号可能为正常轴或者不对中轴的振动信号，因此可以限制在这两种状态内讨论，由图6 得出振动信号的振幅范围为1～116.2，对比表1 并结合图7 的分析结果，得出此振动信号为正常轴的振动信号，排除了故障的可能性，最终对图8 分析，由于图8 中振动信号的振幅范围为12～33.1，对比表1 得出，此振动信号为正常轴的振动信号，验证了图6 和图7 的分析结果，最终得出正确的故障诊断结果。本文通过多频谱综合分析，逐步缩小故障的可能范围，最终得出正确的诊断结果。为了进一步验证多频谱故障诊断分析算法的诊断准确率，分别对四种故障轴的加速度振动信号采样，每种故障采样30 组数据，将诊断结果正确的样本数占总的样本数的比重作为故障诊断准确率，最后对四种故障的诊断准确率求均值，作为总的故障诊断准确率。通过多频谱故障诊断分析算法，得出故障诊断准确率达到80.9%，较单一频谱分析的准确度提高了5.2%，克服了单一频谱分析对部分故障不敏感的缺陷。

3 结束语

本文提出的一种多频谱故障诊断分析算法，以组合式旋转机械实验装置为平台，旋转机械轴的单一故障为研究对象，通过大量旋转机械故障的实验数据分析，从实验结果上可以得出，多频谱故障诊断技术克服了单一频谱分析中故障诊断准确率不高的缺陷，增加了旋转机械故障诊断的准确性和多样性。但目前旋转机械多为复合并发故障，因此在旋转机械多重并发故障的背景下，多频谱分析技术在多重并发故障预测与诊断领域还需要进一步的研究。

［1］王金福，李福才. 机械故障诊断的信号处理方法:频域分析［J］. 噪声与振动控制，2013(1):173 -180.

［2］汪光阳，周义莲. 煤气鼓风机故障诊断的神经网络模型研究与实现［J］. 计算机应用与软件，2011，28(2):90 -92.

［3］黄雪琼. IPTV 故障诊断专家系统设计［D］. 广州:华南理工大学，2012.

［4］李红卫，杨东升，孙一兰，等. 智能故障诊断技术研究综述与展望［J］. 计算机工程与设计，2013，34(4):632 -63.

［5］边霞，米良. 遗传算法理论及其应用研究进展［J］. 计算机应用研究，2010，27(7):2425 -2429.

［6］高文军. 基于人工免疫算法优化支持向量机的电力变压器故障诊断研究［D］. 太原:太原理工大学，2012.

［7］成建生，孙业梅，杨帅，等. 基于频谱分析法对旋转机械故障的诊断［J］. 煤矿机械，2011，32(1):253 -254.

［8］张文，范国敏. 功率谱分析在泵齿轮故障监测中的应用［J］. 煤炭科学技术，2004，32(5):27 -31.

［9］B.Liang. Application of power spectrum，cepstrum，higher order spectrum and neural network analyses for induction motor fault diagnosis［J］. Mechanical Systems and Signal Processing，2013.

［10］李文超. 现代功率谱估计在设备故障诊断应用［J］. 传感器世界，2012(2):25 -29.

［11］邢务强，钮金鑫. 基于AR 模型的功率谱估计［J］. 现代电子技术，2011，34(7):49 -51.

［12］张洋，岳东杰，顾志强，等. 现代谱估计在苏通大桥钢箱梁振动信号分析中的应用［J］. 水利与建筑工程学报，2012，10(2):36 -40.

［13］王旭峰. 基于倒频谱分析法的滚动轴承故障诊断研究［D］. 昆明:昆明理工大学，2010.