大型精密回转工作台传动性能分析研究*

袁胜万，寸花英，李江艳，余正斌

(沈机集团昆明机床股份有限公司，昆明 650203)

0 引言

振动、噪声、传动精度及运动稳定性是研究转台传动系统重点关注的问题，国内外学者针对这些问题已经做了大量工作［1］。哈尔滨工业大学的谢涛采用有限元方法对飞行转台进行结构动力学分析和优化设计，并获得良好的应用［2］;美国J.G.Blance 等人使用纯几何学的方法研究了摆线针轮减速机构的传动精度［3］;苏联勃鲁也维奇提出使用概率统计法对机构的传动精度进行计算，对机构精确度线性理论，机构精确度的计算、概率模拟的应用、随机变量典型分布规律等进行了系统的论述［4］，受业界的肯定与推崇。李圣怡等详细开展了精密和超精密机床精度建模、误差仿真、虚拟加工等工作，并在精密及超精密机床设计上取得良好的应用效果［5］。

本文的研究对象为大型精密回转工作台传动系统，该转台系统为沈机集团昆明机床股份有限公司开发THM65160 精密卧式加工中心工作台，主要针对航空航天、汽车、能源等行业中大重型零部件的加工而设计开发的，该工作台尺寸为1600mm ×1600mm，最大承重为20t，转台定位精度要求9"，重复定位精度要求5";通过调研发现，目前国内外大部分厂家生产的加工中心工作台尺寸绝大部分都在1000mm 一下，能够做到1200mm 的不多，相对于国内外大部分加工中心而言，该转台具有尺寸大，承载高，其传动系统包括蜗杆-蜗轮-小齿轮-大齿圈传动，其传动结构复杂。提升转台系统的定位精度和重复定位精度、静动刚度、动态响应特性及可靠性等是研发大重型精密转台的主要难题，本文针对快速响应特性及转台传动精度两个问题，基于集中参数法及等价误差法建立转台传动系统动力学模型和传动精度模型，对该传动系统动态响应特性和传动精度进行分析，研究和改善影响转台传动系统性能和精度因素，以提高传动系统的承载能力、动态性能及传动精度，为工程实践中传动系统性能提升提高理论参考。

1 精密回转工作台传动系统动力学建模

1.1 精密转台传动系统传动示意图

为了提高传动精度，转台传动系统采用蜗杆蜗轮-小齿轮大齿圈传动，在减少传动链同时尽量增大传动比。传动系统如图1 所示，该系统由电机通过蜗杆蜗轮带动齿轮齿圈，从而驱动回转台转动。

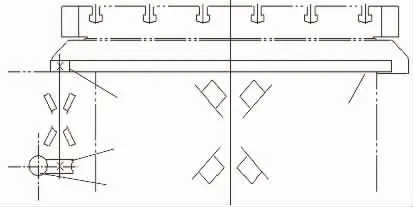
图1 回转工作台传动系统图

图2 回转工作台动力学模型

1.2 精密转台传动系统动力学方程

根据集中参数法建立实际转台传动系统动力学模型［6-7］，传动系统动力学模型如图2 所示，其中Te、Tg分别为电机扭矩，切削负载阻力矩;Ii为各质量块的转动惯量，其中Ie为电机轴的转动惯量，Ig为负载的转动惯量i =1，2，3，4 ;θi为各质量块的扭转角位移，其中θe为电机轴的扭转角位移，θg为输出轴的扭转角位移;i =1，2，3，4 ;ci各个轴的的扭转阻尼，i =1，2，3 ;ki为各个轴的的扭转刚度，i =1，2，3 ;cij/kij为齿轮副的啮合阻尼/啮合刚度;Ri为每个齿轮分度圆半径，i =1，2，3，4，e，g;ei为各个齿轮副的综合传动误差，i =1，2，3 ;其动力学方程如式(1)所示。

1.3 传动系统激励分析

齿轮传动系统的动态激励有内部激励和外部激励两类。内部激励是齿轮传动与一般机械的不同之处，它是由于同时啮合齿对数的变化、轮齿的受载变形、齿轮误差等引起了啮合过程中的轮齿动态啮合力产生的，因而即使没有外部激励，齿轮系统也会受这种内部的动态激励而产生振动噪声。外部激励是指齿轮系统的其它外部因素对齿轮啮合和齿轮系统产生的动态激励。对于原动机和负载运转平稳，齿轮系统加工和装配精度较高时，齿轮内部激励是齿轮系统动态激励主要部分。针对蜗杆-涡轮-浮动小齿轮带动大齿圈回转工作台，我们主要研究齿轮啮合时的内部动态激励［7］。

(1)齿轮副啮合刚度

为了提高计算效率，齿轮的啮合刚度采用国际标准化组织(ISO)在齿轮强度计算公式中推荐公式，计算公式如下:

式中，z1为主动轮的齿数;z2为从动轮的齿数;x1主动轮的法面变位系数;x2为从动轮的法面变位系数。εα为齿轮的端面重合度。b为齿轮的宽度。k即为齿轮的综合啮合刚度。

(2)传动系统的阻尼

传动轴的扭转振动阻尼主要是材料阻力，根据H.H.Lin 和C.Lee 等的分析结论，传动轴的扭转阻尼可表示为:

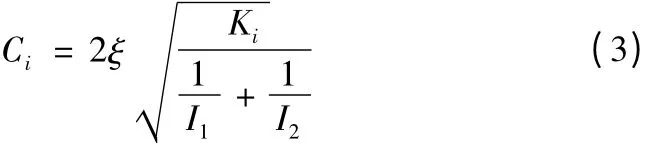
式中，Ki为轴的扭转刚度，I1、I2分别是轴上两质量块的转动惯量，ξ 为阻尼比，根据D. R. Houser 等的试验研究，ξ 一般取值范围为0.005～0.075。

齿轮副的啮合阻尼系数可由下式计算:

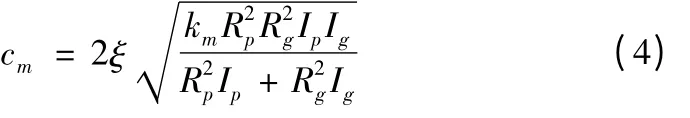
式中，km为一对啮合齿轮副的啮合刚度，Ip、Ig分别是齿轮副主从动轮的转动惯量，Rp、Rg分别是齿轮副主从动轮的半径，ξ 为齿轮啮合的阻尼比，按照R.Kasuba 和K.L.Wang 的分析计算，一般取值范围为0.03～0.07。

(3)误差激励轮齿啮合误差是由齿轮加工误差和安装误差引起的，这些误差使齿轮啮合齿廊偏离理论的理想啮合位置，破坏了渐开线齿轮的正确啮合方式，使齿轮瞬时传动比发生变化，造成齿与齿之间碰撞和冲击，产生齿轮啮合的误差激励。通常，影响齿轮振动噪声的各种因素中，齿距误差和齿形误差的影响最大。啮合传动误差的影响综合反映在啮合线方向，可表示为:

式中ψ(t)为长周期误差函数，φ(t)为短周期误差函数，A为长周期误差的幅值，Bn为短周期误差的幅值，φn为短周期误差的相位角，ω 为回转频率，ωg为啮合角频率。根据齿轮设计的精度等级确定齿轮的偏差，采用简谐函数表示法进行误差模拟，则轮齿的齿形误差和基节误差可用正弦函数表示为:

式中，e0、er分别为轮齿误差的常值和幅值，Tz为齿轮的啮合周期，φ 为相位角。

一般情况下取e0为0，φ 为0，而基节误差fpb和齿形误差ff占齿轮系统误差的70%，是影响齿根应力最重要的加工误差因素，所以取er等于啮合齿对的有效误差。它们是随机变量，并且服从正态分布和差值分布，考虑上述两种主要误差时，啮合齿对的有效误差Δf∑为:

式中，fpb——基节误差，ff——齿形误差

齿轮副精度均为5LM，蜗轮蜗杆的误差值如下表所示:

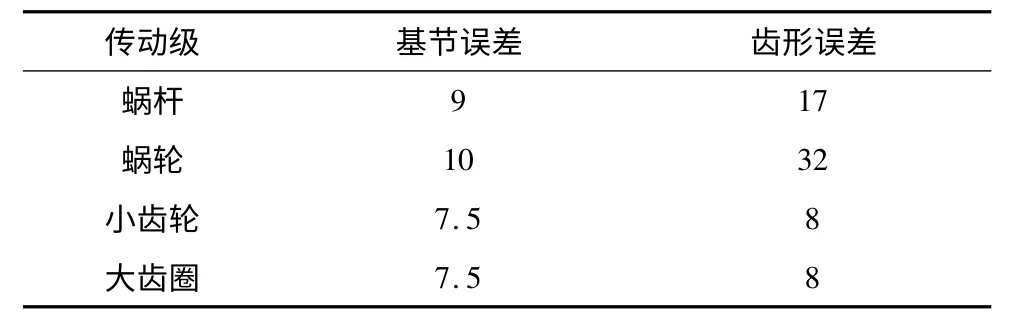
表1 齿轮副误差值(单位:μm)

2 转台系统仿真分析及讨论

针对方程(1)来研究转台系统的动态响应特性，该传动系统的主要参数为

表2 轴的扭转刚度和阻尼

表3 齿轮副的啮合刚度和阻尼

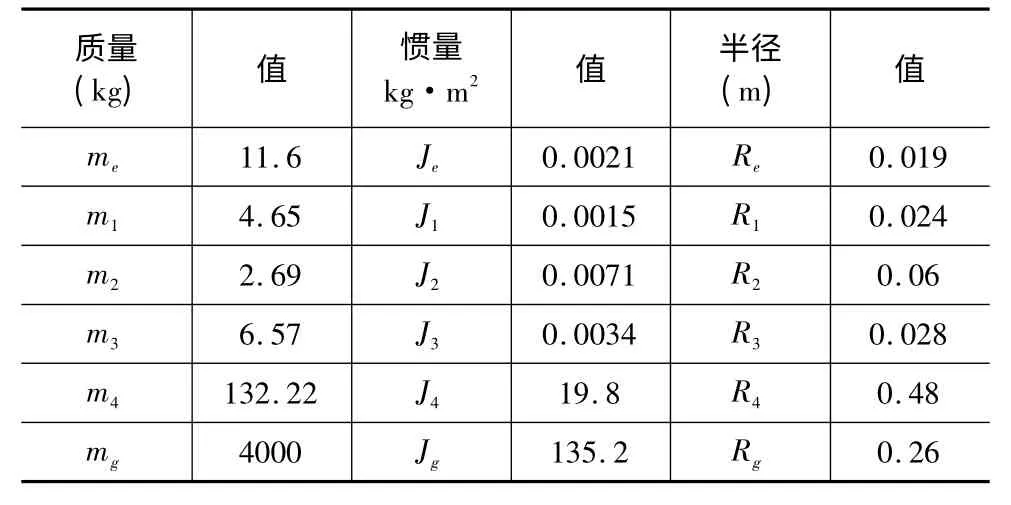
表4 转台传动系统参数

2.1 传动系统动态响应分析

回转工作台的的动力学方程为时变型非线性微分方程，获得传动系统中各齿轮的动态响应。时域响应取0.1s 的响应进行分析。时域响应分析中主要分析齿轮的速度和加速度随时间的变化，由于时域分析不能很好反映系统的特性，所以必须要分析每个齿轮的频域特征。采用Newmark-β 数值方法求解［8-9］，可得到输出蜗轮蜗杆传动副及齿轮齿圈传动副的扭转振动角速度以及角加速度值，如下图所示。

图3 输入轴的振动速度及振动加速度时域曲线

图4 输出轴的振动速度及加速度时域曲线

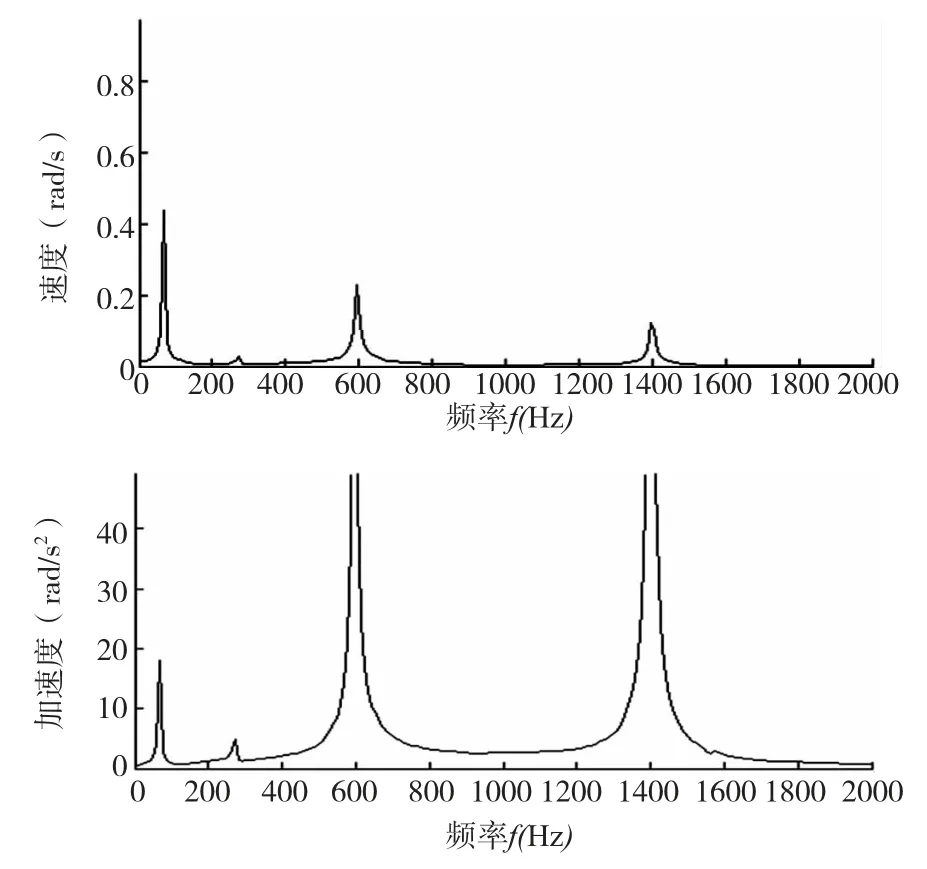
图5 输出轴的振动速度及加速度频域曲线

由频谱图可见，输出轴的频域幅值主要出现在66.67Hz 及其100Hz 倍频上，其中100Hz 为蜗轮蜗杆的啮合频率，66.67Hz 为齿轮齿圈的啮合频率。表明啮合频率对系统振动存在较大影响。

齿轮装置的振动大小是由振动速度的均方值进行评价的。输入、输出轴的振动速度均方根值结果见表5 所示。

表5 输入输出轴振动速度均值

按照GB/T6404.2《齿轮装置的验收规范》对工作台回转传动系统的振动进行评价，输入轴的振动速度均值为4.36 ×10-2，在振动评价曲线中位于A 级水平;输出轴的振动速度均值为8. 06，输入功率为4.0kW，在振动评价曲线中处于C 级水平，表明输入轴在高速输入情况下振动情况良好，而输出轴在高速输入情况下振动情况较差，需要采取一定的措施对其减振，以提高回转工作台的回转动态特性。

3 回转传动精度建模及误差分析

回转传动误差是指对应着同一输入回转角，输出轴的实际回转角与理论回转角之间的差值。若令与电机轴的输入角为θ1，工作台的实际回转角与理论回转角分别为θ'4和θ4，传动比为N，则回转传动误差为:

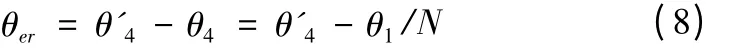
采用等价误差法对精密回转工作台的传动系统进行回转精度建模［10-11］，工作台的回转传动系统同上图1 所示，根据传动结构建立传动精度模型如图6 所示，建模时假设:

①不计齿轮啮合时摩擦力的影响;

②齿轮间的啮合力始终作用在啮合线上;

综合考虑转台各传动零件的等价误差，以及运动的加速度，利用牛顿第二定理建立传动精度数学模型［10］，见方程①～⑥所示。

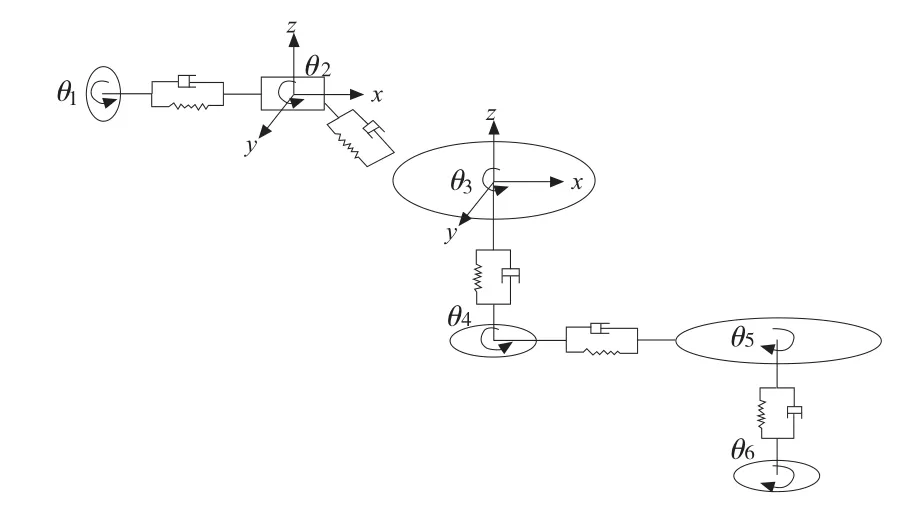
图6 回转工作台的回转精度模型

其中，

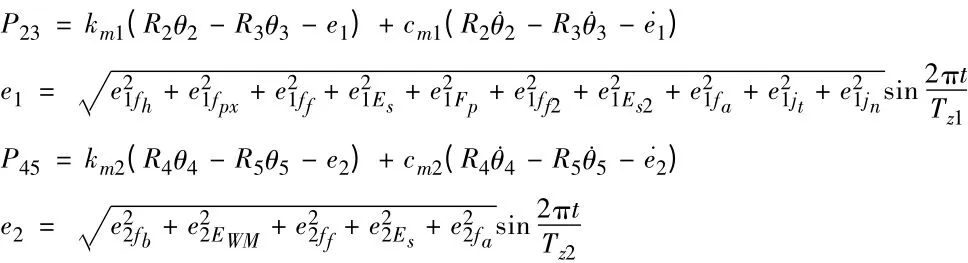
式中，方程①～⑥中各参数意义同方程(1)一致。Tzi齿轮副的啮合频率，i =1，2 ，蜗杆的误差:螺旋线误差fh=9μm，轴向齿距累积误差fpx=10μm，齿形误差ff=9，齿厚偏差Es=19μm;蜗轮的误差:螺旋线误差Fp=9μm，轴向齿距累积误差ff2=μm，齿形误差ff=5，齿厚偏差Es=33.5μm;蜗杆副的误差:中心距偏差fa=45μm，圆周侧隙jt=24.25μm，法向侧隙jn=25μm. 小齿轮的各项误差:齿厚偏差Es=40μm，齿形误差ff=7μm，基节偏差fpb=7μm，法向公法线偏差ΔEWm=12μm;大齿圈的各项误差:齿厚偏差△Es=90μm，齿形误差ff=13μm，基节偏差△fpb=9μm，法向公法线偏差ΔEWm=25μm;齿轮副的各项误差:中心距偏差△fa=35μm。

根据Runge-Kutta［11］法对传动精度方程进行求解，从而得到精密回转工作台回转传动系统的传动精度，输出轴的回转传动误差如下图所示。

图7 输出轴的回转传动误差

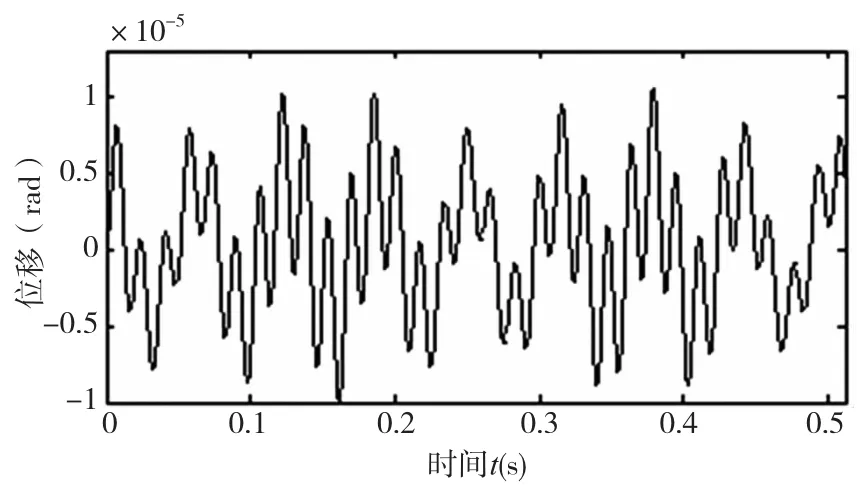
图8 蜗轮蜗杆副对传动精度的影响

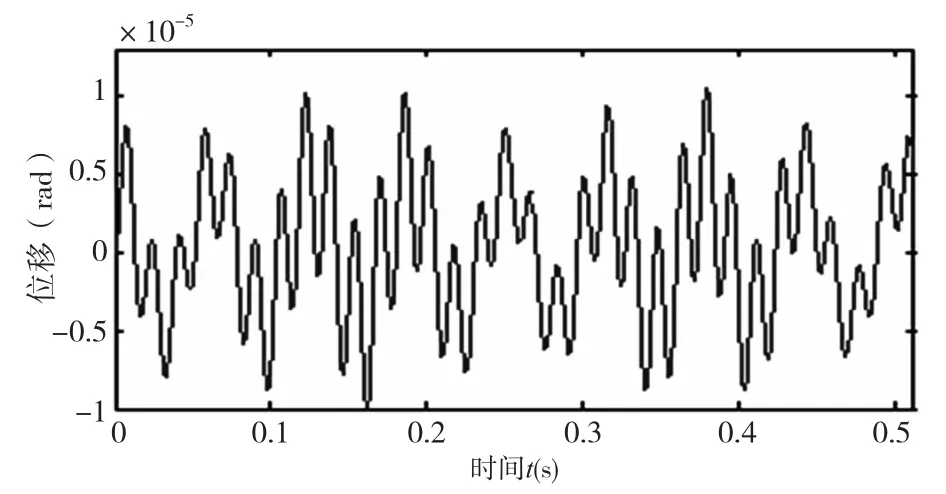
图9 齿轮传动副对传动精度的影响

图7 求得的结果即为输出轴的误差弧度值，当工作台运转稳定后对其传动误差进行分析可知，其传动误差幅值为3 ×10-5rad，转换成角度值为6.19";相邻两个周期的误差幅值的差值约为0.8 ×10-6rad，对其进行角度转换可得0.165"。

浮动小齿轮带动大齿圈回转工作台，要求定位精度达到9"，重复定位精度达到5"。理论分析发现重复定位精度与定位精度均满足验收条件。由于在理论分析中只考虑了齿轮本身的制造误差和安装误差对传动精度的影响，而忽略了其他一些诸如轴承等的制造和安装误差对传动精度的影响，因而理论分析与实际结果是有一定的差距的。所以在回转工作台的设计过程中需要对其回转传动系统进行消隙处理［12］。工程应用中，主要采取的消隙方式有伺服电机、蜗杆蜗轮机构及小齿轮组成的回转工作台驱动机构浮动安装在滑座上，可自动消除小齿轮与大齿圈之间的间隙并补偿齿轮齿圈的中心距误差。提高齿轮齿圈的制造和安装精度等方式进行消隙，提高其传动精度。

3 结论

本文建立了一种浮动小齿轮带动大齿圈回转工作台动力学模型和传动精度模型，系统地研究了精密转台在自激作用下下的动态响应和传动精度及其影响因素，其结论如下.

(1)利用Newmark-β 数值方法求解得出了弧齿锥齿轮传动系统的的动态响应，分析表明，啮合频率对系统振动存在较大影响。同时，输入轴在高速输入情况下振动情况良好，而输出轴在高速输入情况下振动情况较差，需要采取一定的措施对其减振，以提高回转工作台的回转动态特性。

(2)针对影响机构传动精度的各零件的加工误差和装配误差等因素进行建模分析，理论分析发现重复定位精度与定位精度均满足验收条件。通过与实际测试结果对比发现，由于理论分析忽略了其他一些诸如轴承等的制造和安装误差对传动精度的影响因素，其分析结果与测试结果有一定差距，需要对转台进行消隙处理，以进一步提高其传动精度。

［1］Kang C H，Hsu W C，Lee E K，et al . Dynamic analisis of gear-rotor system with viscoelastic supports under residual shaft bow effect［J］.Mechanism and Machine Theory，2011，46(3):264 -275.

［2］谢涛.飞行仿真转台结构动力学分析及其优化设计研究［D］，哈尔滨:哈尔滨工业大学，2003.

［3］Blanche J G，Yang D C H，Cyeloid drives with machining toler-ances［J］. Journal of Mechanisms，Transmisslons，and Antomation in Design，1989，111(9):337 -344

［4］Y.Cheng，T.C.Lim.Vibration Analysis of Hypoid Transmissions Applying an Exact Geometry-based Gear Mesh Theory.Journal of Sound and Vibration，2001，240(3):519 -543.

［5］李圣怡，戴一凡，尹自强，等，精密和超精密机床精度建模技术［M］，长沙:国防科技大学出版社，2007.

［6］郜浩冬，张以都，吴琼，等.汇流传动齿轮-转子-轴承系统非线性动力学分析［J］. 振动与冲击，2013，32(8):105 -113，127.

［7］张金海，刘更，周建星，等，考虑啮入冲击作用下减速器的振动 噪声分析［J］.振动与冲击，2013，32 (13):118 -122，141.

［8］冯领香，魏建国，王森林，等. 一种可自调步长的改进Newmark 算法［J］. 河北农业大学报，2004，27 (3):111 -114.

［9］朱才朝，罗召霞，刘明勇，等. 新型定轴摆轮减速传动分析［J］. 重庆大学学报，2010(3):7 -12.

［10］李军，李润方，林超，等. 小模数精密齿轮传动误差分析及实验研究［J］. 机械，2003，30(7)，15 -17.

［11］韩林山，谭群燕，沈允文，等. 间隙及转矩对2K-V 型传动装置传动精度的影响［J］. 机械科学与技术，2007，26(8):1080 -1089.