钢锚梁索塔锚固区混凝土塔壁简化计算方法

贺国栋，石雪飞

（同济大学桥梁工程系，上海 200092）

1 锚固区简化计算基本思想

钢锚梁索塔锚固体系［1－2］是一种典型的钢－混凝土组合结构锚固方式，其一般构造形式如图1所示。

在钢锚梁锚固体系中，锚固横梁支承于空心塔柱内壁的牛腿凸块上，斜拉索穿过预埋在塔壁中的钢管锚固，固定在钢锚固梁两端的锚块上。斜拉索的竖向分力通过钢锚梁的垂直支撑板传递至牛腿，再由牛腿凸块传递给塔柱；拉索的水平分力则大部分由钢锚梁本身承担，另一部分由混凝土塔壁承担［3－4］。

对钢锚梁锚固体系进行传力路径分析可知：虽然钢锚梁、牛腿及塔壁三者是一个共同工作体系，但进行受力分析时，可以将它们分别当做独立的构件来考虑，即合理模拟边界条件，分别独立考虑钢锚梁、混凝土牛腿及混凝土塔壁的设计和计算。

锚固区混凝土塔壁的水平受力性能直接影响其配筋计算和结构尺寸的确定。塔壁的横向受力复杂，空间效应明显，采用三维实体有限元进行分析。然而，平面杆系结构作为土木工程中最简单也最实用的简化结构，便于工程师掌握，因此，提出塔壁的杆系简化计算方法也尤为必要。索塔锚固区的斜拉索是沿塔高方向等间距离散分布的，若取其中标准索距高度的桥塔节段进行简化框架分析，用于混凝土塔壁水平配筋的预估和检验，既能反映锚固区的实际受力情况，又简化了计算分析对象［5］（如图2所示）。

图2 索塔锚固区及标准节段Fig.2 Anchorage zone and standard segment

作者拟通过理论分析，提出钢锚梁索塔锚固区混凝土塔壁的简化计算方法，并针对其中的关键问题进行研究，为同类结构设计提供参考和借鉴。

2 锚固区水平荷载分配关系

要进行混凝土塔壁的简化分析，必须确定水平荷载在钢锚梁和塔壁中的分配关系，并确定混凝土塔壁具体承担了多少水平力。

2.1 水平荷载传递路径

通过钢锚梁锚固结构在国内、外的应用情况调研，钢锚梁与牛腿的连接形式包括3种［6］：①滑动连接，即钢锚梁与牛腿之间设四氟乙烯板，两者之间可相对滑动，并在钢锚梁与塔壁之间设置挡块以传递部分水平荷载；②固定连接，即钢锚梁与牛腿顶面预埋钢板通过焊缝或高强螺栓固定连接；③斜拉索张拉过程钢锚梁与牛腿一端固定，另一端滑动，拉索锚固后再将两端固定连接。

由钢锚梁锚固体系的构造特点可知，索塔锚固区的水平荷载分配与锚固结构的构造形式和施工方法有关。因此水平荷载的分配关系要分3种情况讨论。

1）当钢锚梁与牛腿的连接方式处于滑动状态时，若不考虑四氟乙烯板表面摩擦力［7］，钢锚梁可以沿纵桥向滑动，斜拉索的平衡水平分力由钢锚梁自身承担，不平衡水平力由挡块传递给混凝土塔壁承担。

2）当钢锚梁与牛腿的连接方式处于固定状态时，由于钢锚梁与端塔壁顺桥向共同变形，结构体系超静定，水平荷载分配应根据变形协调原则由钢锚梁和混凝土塔壁分配承担。

3）当钢锚梁与牛腿的连接方式处于一端固定、另一端滑动时，斜拉索的平衡水平分力由钢锚梁自身承担，不平衡水平力由挡块传递给混凝土塔壁承担。

由此可见，当连接方式为滑动状态或者一端固定、另一端滑动状态时，钢锚梁锚固体系的水平荷载分配关系较为简单，通过简单计算即可得到由钢锚梁和塔壁分别承担的水平荷载。基于变形协调原则，研究钢锚梁与牛腿固定连接的锚固体系的水平荷载分配计算方法。

2.2 水平荷载分配计算方法

在锚固区，选取标准索距高度的桥塔节段。将混凝土塔壁简化为平面框架。将钢锚梁简化为水平拉杆，仅承受轴力，其大小记为2Ps。将作用于塔壁的水平荷载简化为均布线荷载，左侧荷载集度为qa，右侧荷载集度为qb，分别如图3，4所示。

图3 两端固定体系受力示意Fig.3 Layout of the fixed system

图4 索塔锚固区框架模型Fig.4 Framework model of the anchorage zone in pylon

考虑到桥梁运营过程的不平衡活载以及换索和断索等情况，桥塔两侧斜拉索的水平分力Fx1和Fx2不一定完全相等，从而最终作用于两侧塔壁的水平荷载也不一定相等，即qa≠qb。将荷载分解为正对称q1和反对称q2，则q1＝（qa＋qb）／2，q2＝（qa－qb）／2，结构在正、反对称荷载作用下的变形如图5所示。在正对称荷载q1作用下，左、右两边的端塔壁向相反方向弯曲变形，同时钢锚梁伸长；在反对称荷载q2作用下，左、右两边的端塔壁向相同方向弯曲变形，相对位移为零，钢锚梁不伸长，因此，钢锚梁轴力为零。故反对称荷载完全由混凝土塔壁承担，钢锚梁不受力，只需要对正对称荷载作用的情况进行分配计算，可取四分之一结构，如图6所示。

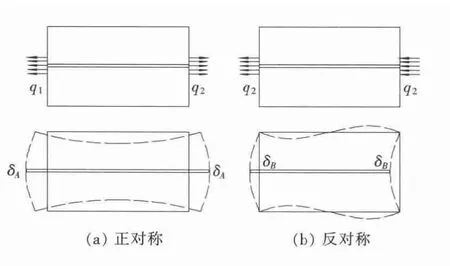
图5 正、反对称荷载下结构变形示意Fig.5 Deformation of positive symmetric and skew－symmetric structures

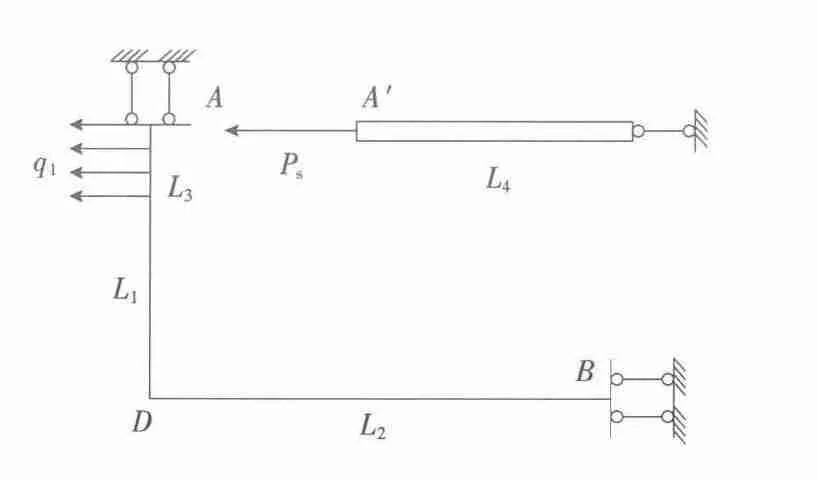
图6 正对称四分之一结构简化模型Fig.6 Simplified quarter structure model

在图6中，AD表示端塔壁，BD表示侧塔壁。假设其弹性模量为Ec，半结构长度为L1和L2，壁厚t1和t2，截面面积为A1和A2，抗弯惯性矩为I1和I2；钢锚梁拉杆的弹性模量为Es，半结构长度为L4，截面面积为As；作用于端塔壁的线荷载分布长度为L3（对于滑动连接的结构，可取钢锚梁与塔壁之间的挡块宽度；对于固定连接的结构，可取钢锚梁与牛腿顶面预埋件之间的焊缝长度）。

经简化的1／4框架结构为一次超静定，可以用力法求解，得到结构的弯矩图，再利用图乘法求得端塔壁A点的顺桥向位移。不妨设单位荷载q＝1作用下，A点顺桥向位移为δ，则q1引起的位移为δA＝q1δ，其中，经计算后δ的表达式为：

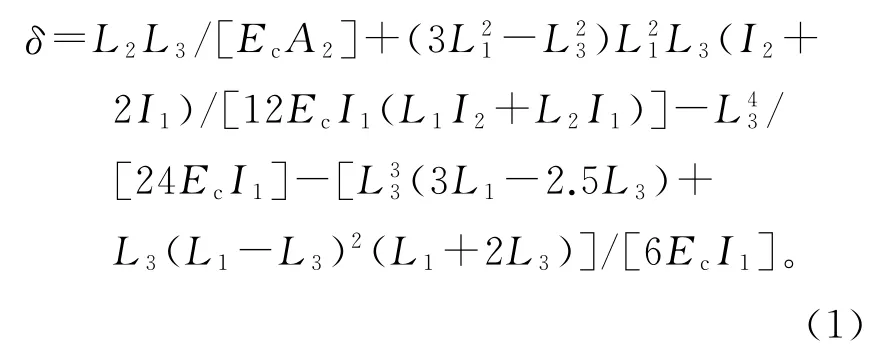
钢锚梁在水平拉力Ps的作用下伸长，其端部A′点的顺桥向伸长量为：

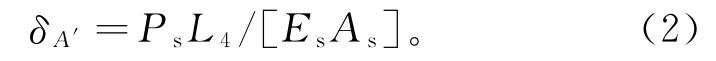
根据变形协调原理，δA＝δA′，则钢锚梁轴力的1／2为：

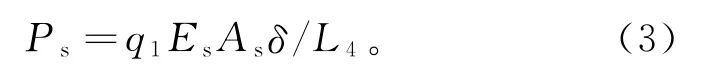
由对称性可知，整个钢锚梁承受的水平力为：

由于通过钢锚梁传递至塔壁的水平荷载与塔壁对钢锚梁的反力是一对作用力与反作用力，两者大小相等。若两侧斜拉索的水平分力为Fx1和Fx2，取钢锚梁为研究对象，可建立平衡方程组：

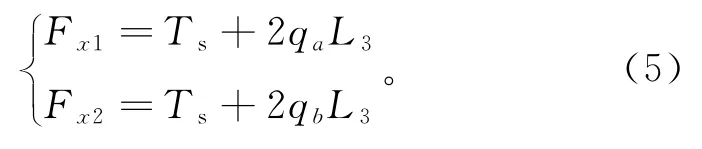
将Ts的表达式代入方程组，并假设Fx2＝kFx1，解得：

其中La＝EsAsδ／L4，物理意义为q＝1引起的钢锚梁轴力的1／2。

将qa和qb回代Ts表达式，得：

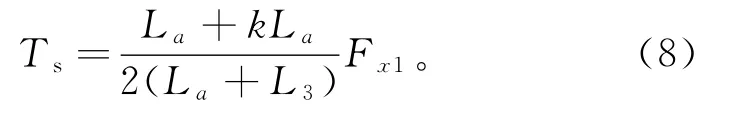
两侧混凝土塔壁承担的水平力为：

因此，得：

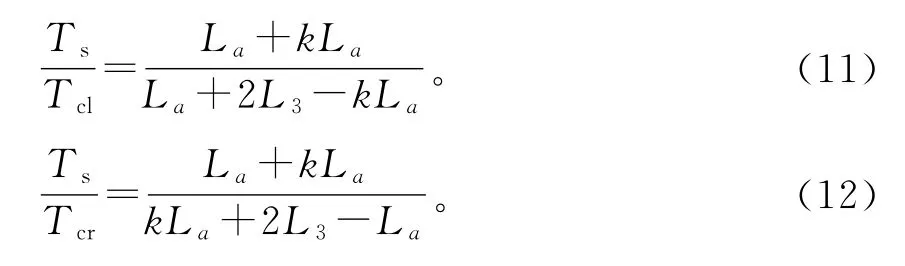
式（11）和式（12）即表示固定连接的钢锚梁锚固体系在水平荷载作用下混凝土塔壁和钢锚梁之间的荷载分配关系。

特别地，当两侧水平荷载大小相等（即Fx1＝Fx2＝F）时，则k＝1，式（11）和式（12）可简化为：

2.3 与有限元计算的对比

为了验证简化公式的准确性，针对某桥钢锚梁索塔锚固区的具体结构，首先，按照简化公式，计算水平荷载分配关系；然后，利用Ansys有限元程序，建立锚固区的空间有限元模型，进行荷载分配分析；比较两者计算结果，进行误差分析。

锚固区的空间有限元模型如图7所示。采用Solid45实体单元模拟混凝土塔壁，采用shell63壳单元模拟钢锚梁，水平荷载施加在钢锚梁端板上。根据计算结果，采用应力积分法，求解钢锚梁的轴力Ts。

简化公式的计算结果和有限元计算结果比较接近，其误差约为6.5%，仍在可接受范围之内。这表明本研究所提出的荷载分配简化计算公式具有较好的准确性。

图7 锚固区Ansys有限元模型Fig.7 Ansys finite element model for the anchorage zone

3 混凝土塔壁的框架简化计算

明确了水平荷载的分配关系后，在给定的索力设计值作用下，即可得到塔壁所承受的水平力。通过对塔壁受力分析可知，在水平力作用下，端塔壁处于弯曲受力状态，侧塔壁处于偏心受拉状态。将两侧荷载分解为正对称和反对称，根据结构的对称性，其1／4简化受力模型分别如图8～9所示。

图8 正对称四分之一塔壁简化模型Fig.8 Simplified symmetric positive 1／4model

图9 反对称四分之一塔壁简化模型Fig.9 Simplified anti symmetric 1／4model

对框架模型进行简单受力分析可知：端塔壁受弯为主，受弯最不利的位置是端塔壁中间位置，即A截面；侧塔壁偏心受拉为主，受拉最不利的位置是侧塔壁端部位置，即D截面。从而A，D截面均为验算结构承载力和抗裂性的控制截面。经计算，荷载综合作用下，A，D截面的弯矩和轴力分别为：

得到控制截面的弯矩和轴力后，进行内力组合就可以进行塔壁的配筋设计和验算。

为验证混凝土塔壁简化框架计算方法的可行性，将采用框架模型算出的弯矩和轴力与采用空间实体模型积分得到的弯矩和轴力进行对比，弯矩误差约为8.3%，轴力误差约为6.2%。这表明本研究所提出的简化框架计算方法具有一定的工程意义。

4 结论

通过对钢锚梁索塔锚固区的构造特性分析和混凝土塔壁的简化计算，得出的结论为：

1）锚固区的水平荷载分配与结构的构造形式和施工过程有关。

2）推导了固定连接方式的锚固体系在斜拉索水平分力下钢锚梁与混凝土塔壁的荷载分配计算公式。并将简化计算公式与有限元分析进行验证，其误差约为6.5%。这表明该简化计算公式具有较好的准确性。

3）推导了水平荷载作用下混凝土塔壁控制截面的内力计算公式，并将简化计算公式与有限元分析进行对比，其误差较小。这表明作者提出的简化框架计算方法具有一定的工程意义。

（References）：

［1］邵旭东.桥梁工程［M］.北京：人民交通出版社，2007.（SHAO Xu－dong.Bridge engineering［M］.Beijing：China Communications Press，2007.（in Chinese））

［2］张喜刚，刘玉擎.组合索塔锚固结构［M］.北京：人民交通出版社，2010.（ZHANG Xi－gang，LIU Yu－qing.Cable－tower composite anchorage［M］.Beijing：China Communications Press，2010.（in Chinese））

［3］华新.斜拉桥索塔钢锚箱与塔壁混凝土拉力分配简化分析［J］.现代交通技术，2006，3（1）：26－29.（HUA Xin.Simplified method about tension distributing between steel anchorage box and concrete pylon wall on the anchorage section of pylon of cable－stayed bridges［J］.Modern Transportation Technology，2006，3（1）：26－29.（in Chinese））

［4］杨忠明，王庆曾.灌河特大桥钢锚梁安装［J］.桥梁建设，2006（S1）：60－62.（YANG Zhong－ming，WANG Qing－zeng.Installation of steel anchor beams of Guanhe river bridge［J］.Bridge Construction，2006（S1）：60－62.（in Chinese））

［5］汪昕，吕志涛.斜向索力下钢－混凝土组合索塔锚固区荷载传递与分配关系分析［J］.东南大学学报：自然科学版，2006，36（4）：585－589.（WANG Xin，LV Zhi－tao.Load transfer and the distribution in the anchorage zone of stell－concrete composite pylon under cable forces［J］.Journal of Southeast University：Natual Science Edition，2006，36（4）：585－589.（in Chinese））

［6］胡贵琼，郑舟军.荆岳长江公路大桥钢锚梁索塔锚固区单节段模型有限元分析［J］.世界桥梁，2010（3）：40－44.（HU Gui－qiong，ZHENG Zhou－jun.Finite element analysis of single sectional model of cable to pylon steel anchor beam zone of Jingyue Changjiang River Highway Bridge［J］.The World Bridge，2010（3）：40－44.（in Chinese））

［7］张奇志，尹夏明，郑舟军.钢锚梁索塔锚固区受力机理分析与约束方式比选［J］.桥梁建设，2012，42（6）：50－56.（ZHANG Qi－zhi，YIN Xia－ming，ZHENG Zhou－jun.Analysis of force mechanism and comparison of restraint ways for steel anchor beam anchorage zone in pylon［J］.Bridge Construction，2012，42（6）：50－56.（in Chinese））