关于伪Smarandache函数的一个下界估计

鲁伟阳， 高 丽， 郝虹斐， 王曦浛

(延安大学 数学与计算机科学学院， 陕西 延安 716000)

0 引言

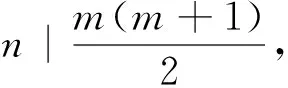
关于Z(n)的初等性质，许多学者曾经研究过，并获得了不少有意义的结果[1-5]. 例如,Yuanbing Lou[3]研究了一个包含伪Smarandache函数的均值问题，得到了一个渐近式：

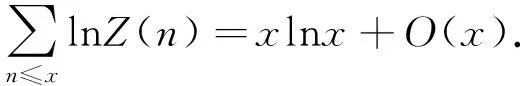
Lin Cheng[4]讨论了一个包含伪Smarandache函数的均值，得到了一个渐近式：

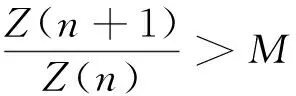
Le Maohua在文献[6]中研究了S(2p-1(2p-1))的下界估计问题，并给出估计式:

S(2p-1(2p-1))≥2p+1

其中,S(n)为著名的Smarandache函数.

苏娟丽[7]改进了文献[6]的结论，得到了更强的下界估计.即对任意的素数p≥7，有估计式:

S(2p-1(2p-1))≥6p+1.

苏娟丽还在文献[8]中研究了S(2p+1)的下界估计问题，证明了对任意的素数p≥7，有估计式

S(2p+1)≥6p+1.

温田丁[9]证明了对任意的素数p≥7,有估计式S(2p-1)≥10p+1,S(2p+1)≥10p+1.

事实上，上述文献所提到的数列Mp=2p-1就是著名的梅森尼(Mersenne)数.梅森尼曾经猜想对所有的素数p，Mp均为素数.这一猜想后来被验证是错误的，因为M11=211-1=23×89是合数.而数列2p-1(2p-1)与一个古老的数论难题——偶完全数密切相关，其相关内容可参阅文献[9,10].

受文献[6-9]的启发，本文利用初等方法研究了伪Smarandache函数Z(n)在2p+1与2p-1上的下界估计问题，并得到了较强的下界估计.

1 相关引理

引理1[11,12]对任意的素数p≥3及k∈N，Z(pk)=pk-1.当p=2时，Z(2k)=2k+1-1.

引理2[11]若n为任意合数，则

Z(n)=max{Z(m):m|n}.

2 主要结论及其证明

定理对任意的素数p≥17，我们有估计式

(Ⅰ)Z(2p+1)≥10p；(Ⅱ)Z(2p-1)≥10p.

证明:由引理2可知，对任意的素数p|n，有Z(n)≥Z(p)=p-1，且(p-1)|Z(pα)对所有的正整数α均成立.

2.1 关于定理中(Ⅰ)式的证明

因为2≡-1(mod 3)，22≡1(mod 3)，且对任意的奇素数p，有2p≡-1(mod 3)，即2p+1≡0(mod 3),这说明对任意的奇素数p，2p+1都有素因子3.

当p≥17时，先证2p+1不可能是3的m次幂(m∈N).假设2p+1是3的m次幂，则有2p+1=3m.当m=2k+1时，有1≡2p+1≡3m≡32k+1≡3(mod 8)矛盾；当m=2k时，2p=3m-1=(3k+1)(3k-1).又(3k+1,3k-1)=2，可得3k-1=2,k=1,这与p≥17矛盾.因此，2p+1不可能是3的m次幂.由此可知，2p+1至少含有一个大于3的素因子.

对任意的素数p≥17，设q为2p+1的任一大于3素因子，则有q≥5.由伪Smarandache函数Z(n)的性质可知:

Z(2p+1)≥q-1

(1)

又q|2p+1，则有2p+1≡0(modq)，即2p≡-1(modq).此时,可设m为2模q的指标，则2m≡1(modq).由2p≡1(modq)可得22p≡1(modq),所以由指标的性质[10,14]知：m|2p.于是有m=1,2,p,2p，显然m≠1,2,p，所以m=2p.又由指标的性质[10,14]可知：m|φ(q)=q-1，即q-1=m·k=2p·k，亦即:

q=2kp+1,k=1,2,3,…

(2)

因此，2p+1可以分为以下4种情况：

(1)若2p+1除3之外含有一个大于3的素因子q.此时有4种可能:2p+1=3α·(2p+1)β或者2p+1=3α·(4p+1)β或者2p+1=3α·(6p+1)β或者2p+1=3α·(8p+1)β.

如果2p+1=3α·(2p+1)β成立，则当β≥5时，有Z(2p+1)≥Z((2p+1)β)≥β·[(2p+1)-1]≥5·[(2p+1)-1]≥10p.

当β=4时，若α为偶数(设α=2k)，则2p+1=32k·(2p+1)4，即2p+1为完全平方数.设2p+1=a2，则2p=a2-1=(a+1)(a-1).然而(a+1,a-1)=2，可知a-1=2，即a=3.所以p=3，这与p≥17矛盾.故α不可能是偶数；若α为奇数(设α=2k+1)，则2p+1=32k+1·(2p+1)4,由于1≡2p+1=32k+1·(2p+1)4≡3(mod 8)矛盾，所以2p+1≠32k+1·(2p+1)2，即α也不可能为奇数.因此β=4不可能成立.

当β=3时，若α为偶数(设α=2k)，则2p+1=32k·(2p+1)3，2p=32k·(2p+1)3-1=32k·(8p3+12p2+6p)+(3k+1)·(3k-1).

因为4|2p，4|(3k+1)·(3k-1)，4⫮32k·(8p3+12p2+6p)，所以α不可能是偶数.

若α为奇数(设α=2k+1)，则2p+1=32k+1·(2p+1)3.当k=0时，且p≥17,有2p+1>3·(2p+1)3;当k≥1时，2p+1≡32k+1·(2p+1)3≡0(mod 32),则有22p≡1(mod 32).此时,可设n为2模q的指标，则2n≡1(modq).由指标的性质[10,14]知：n|2p.于是有n=1,2,p,2p,显然n≠1,2,p，所以n=2p.又由指标的性质[10,14]可知：n|φ(9)=6，即2p|6，p|3,这与p≥17矛盾，所以α也不可能是奇数.因此,β=3不可能成立.同理可知β不可能为1和2.

类似的可证：2p+1=3α·(4p+1)β或2p+1=3α·(6p+1)β或2p+1=3α·(8p+1)β时结论成立.

(2)若2p+1除3之外恰好含有两个大于3的不同的素因子.由式(2)可知，2p+1中不可能同时含有素因子2p+1和4p+1(因为当素数p>3时，2p+1和4p+1中至少有一个能被3整除，所以它们不可能同时为素数).同理,2p+1也不可能同时含有素因子4p+1和8p+1.

因此，由式(2)可设2p+1=3α·(2p+1)β·(6p+1)γ或2p+1=3α·(2p+1)β·(8p+1)γ或2p+1=3α·(4p+1)β·(6p+1)γ.

若2p+1=3α·(2p+1)β·(6p+1)γ成立，则当β≥5或γ≥2时，有Z(2p+1)≥β[(2p+1)-1]≥10p或Z(2p+1)≥γ[(6p+1)-1]≥10p.

类似的可证：当p≥17时，2p+1=3α·(2p+1)β·(8p+1)γ与2p+1=3α·(4p+1)β·(6p+1)γ有结论Z(2p+1)≥10p成立.

(3)若2p+1除3之外恰好含有三个大于3的不同的素因子.若其中至少有一个素因子可以满足等式q=2kp+1且k≥5，显然有Z(2p+1)≥q-1≥2kp≥10p成立.若所有的素因子中的k≤4，因为2p+1和4p+1不可能同时为素数，4p+1和8p+1也不可能同时为素数，故可设：

2p+1=3α·(2p+1)β·(6p+1)γ·(8p+1)δ,

当β≥5或γ≥2或δ≥2 时，定理中(Ⅰ)显然成立.

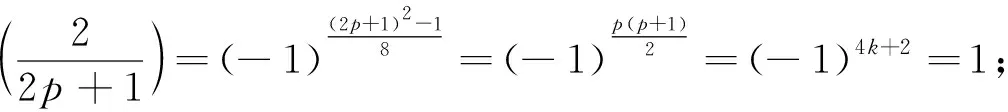
(4)若2p+1除3之外至少含有四个大于3的不同的素因子，由式(2)可知，至少有一个素数满足q=2kp+1且k≥5(因为若k<5，则有q=2p+1，4p+1，6p+1，8p+1，然而2p+1和4p+1不可能同时为素数，4p+1和8p+1也不可能同时为素数，所以k≥5),此时有Z(2p+1)≥q-1≥2kp≥10p显然成立.

综上所述，我们完成了定理中(Ⅰ)式的证明.

2.2 关于定理中(Ⅱ)式的证明

对任意的素数p≥17，设q为2p-1的任一大于3素因子，由伪Smarandache函数Z(n)的性质可知:

Z(2p-1)≥q-1.

(3)

类似于(Ⅰ)式证明可知式(2)成立.显然，2p-1不可能是完全平方数(反证法：假设2p-1是一个完全平方数，可设2p-1=a2，即2p=a2+1,0≡2p≡a2+1≡2(mod 4)矛盾),因此，2p-1可分为以下5种情况：

(1)若2p-1为素数，则由p≥17及Z(n)的性质可知，Z(2p-1)≥2p-2≥10p成立.

(2)若2p-1恰好为素数q的m次幂(其中m≥3)，即2p-1=qm.因为2p-1不可能为完全平方数，所以m=3,5,7,….当m=3时，则q=2kp+1且k≥2，有Z(2p-1)≥Z(q3)=q3-1>3(q-1)≥3[(4p+1)-1]>10p成立.而当p≥17时，显然有2p-1>(2p+1)3，因此2p-1≠(2p+1)3;当m≥5时，由式(2)和式(3)可知Z(2p-1)≥qm-1>m(q-1)≥5[(2p+1)-1]≥10p成立.

显然,当α≥5或β≥2时，有Z(2p-1)≥α[(2p+1)-1]≥10p或Z(2p-1)≥β[(6p+1)-1]≥10p.

当β=1,1≤α≤4时，有2p-1=(2p+1)α·(8p+1)或2p-1=(4p+1)α·(6p+1).

若2p-1=(2p+1)α·(8p+1),当α=4时，因为-1≡2p-1≡(2p+1)4·(8p+1)≡1(mod 8)矛盾，所以α≠4；而当2p-1=(4p+1)3·(6p+1)时，Z(2p-1)≥3[(4p+1)-1]>10p显然成立；此时不妨设1≤α≤3，当p≥17时,有2p-1>(2p+1)3·(8p+1)与2p-1>(4p+1)2·(6p+1),所以2p-1=(2p+1)3·(8p+1)和2p-1=(4p+1)2·(6p+1)不可能成立.所以，当2p-1恰有两个不同的素因子时，有Z(2p-1)≥10p成立.

(4)若2p-1恰有三个不同的素因子.若其中至少有一个素因子可以满足等式q=2kp+1且k≥5，显然有Z(2p-1)≥q-1≥2kp≥10p成立.若所有的素因子中的k≤4，因为2p+1和4p+1不可能同时为素数，4p+1和8p+1也不可能同时为素数，故可设2p-1=(2p+1)α·(6p+1)β·(8p+1)γ,此时，当α≥5或β≥2或γ≥2时,定理中(Ⅱ)式显然成立.

不失一般性，可设2p-1=(2p+1)α·(6p+1)·(8p+1),其中1≤α≤4.由引理3和二次剩余的性质可知，2是素数2p+1和6p+1的二次剩余，然而由上述2.2中(3)的讨论可知，2是2p+1和6p+1的二次非剩余，故矛盾.所以，当2p+1恰有三个不同的素因子时，有Z(2p-1)≥10p成立.

(5)若2p-1至少有四个不同的素因子，同(Ⅰ)式证明过程中(4)及式(2)可知，至少有一个素数满足q=2kp+1且k≥5，此时Z(2p-1)≥q-1≥2kp≥10p显然成立.

综上所述，我们完成了定理中(Ⅱ)式的证明.

3 结束语

有关Smarandache函数的下界估计问题，已经有了不少的研究成果，然而对于伪Smarandache函数的相关内容却并没有涉及.本文在文献[6-9]的基础上，利用初等及组合方法对伪Smarandache函数的下界估计问题进行了研究，拓宽了伪Smarandache函数在下界估计问题方面的研究.

[1] Kashihara Kenichiro.Comments and topics on Smarandache notions and problems[M].USA:Erhus University Press,1996.

[2] A.A.K.Majumdar.A note on the Pseudo-Smarandache function[J].Scientia Magna,2006,2(3):1-25.

[3] Yuanbing Lou.On the Pseudo-Smarandache function[J].Scientia Magna,2007,3(4):48-50.

[4] Lin Cheng.On the mean value of the Pseudo-Smarandache function[J].Scientia Magna,2007,3(3):97-100.

[5] Yani Zheng.On the Pseudo-Smarandache function and its two conjectures[J].Scientia Magna,2007,3(4):74-76.

[6] Le Maohua.A lower bound forS(2p-1(2p-1))[J].Smarand-ache Notions Journal,2001,12(1/2/3):217-218.

[7] 苏娟丽.关于Smarandache函数的一个下界估计[J].纺织高校基础科学学报，2009,22(1)：133-134

[8] 苏娟丽.关于Smarandache函数的一个新的下界估计[J].纯粹数学与应用数学，2008,24(4)：706-708.

[9] 温田丁.Smarandache函数的一个下界估计[J].纯粹数学与应用数学，2010,26(3)：413-416.

[10] Tom M.Apostol.Introduction to analytic number theory[M].New York: Spring Verlag,1976.

[11] 马 荣.Smarandache函数及其相关问题研究[M].USA:The Educational Publisher,2012.

[12] Richard Pinch.Some properties of the Pseudo-Smarandache function[J].Scientia Magna,2005,1(2):167-172.

[13] 潘承洞，潘承彪.初等数论[M].2版.北京：北京大学出版社,2003.

[14] 张文鹏.初等数论[M].西安：陕西师范大学出版社,2007.