基于改进的DE算法对PID参数的优化

蔺小林， 邓雄峰

(1.陕西科技大学 电气与信息工程学院， 陕西 西安 710021； 2.陕西科技大学 陕西省造纸技术及特种纸品开发重点实验室， 陕西 西安 710021 )

0 引言

PID控制器作为一种经典的控制器，由于其原理简单，使用方便，被广泛地应用于工业过程控制系统中.PID控制器虽然不依赖于对象模型，却受其比例系数(Kp)、微分系数(Ki)、积分系数(Kd)影响较大.怎样才能获得PID参数的最优组合，工程中整定PID参数出现过凭借经验调试的经验方法，利用理论公式设计的理论方法，以及加入智能算法的智能搜索方法.目前，利用智能方法研究PID参数整定已成为一大热点，例如模糊控制算法、神经网络算法、遗传算法，蚁群优化算法等都已用在了PID参数整定研究之中.

差分进化算法(Differential Evolution，DE)是Rainer Storn和Kenneth Price在1996年为求解切比雪夫多项式而提出的一种方法[1]，是一种基于群体差异的启发式随机搜索方法，原理简单，受控参数少.这种差分进化算法由于具有较强的全局搜索能力及高效的收敛性、鲁棒性等优点，从而在约束、离散优化计算、化工、机器人、信号处理、系统辨识等方面得到广泛的应用[2].

本文在标准差分进化算法的基础上进行了改进，提出一种自调整放缩因子(F)的改进DE算法，结合性能指标函数(ITAE)，将这种新的方法应用于PID参数的优化设计，并进行了实例仿真.

1 标准差分进化算法概述

1.1 标准差分进化算法的基本原理

差分进化算法是一种基于群体的演化算法，基本思想在于应用当前种群个体的差异来重新组合，通过交叉操作、选择操作，得到中间群体，然后应用于子代和父代个体竞争来获得新一代种群[3-5].

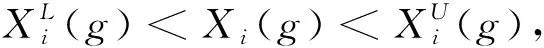
(1)生成初始种群：

采用公式(1)产生初始种群：

(1)

其中rand(0,1)是[0,1]服从均匀分布的随机数.

(2)变异操作

变异操作是差分进化算法中的关键步骤，是从种群NP中随机选择3个个体，设为a1,a2,a3,并且a1≠a2≠a3≠i，则：

hij=xa1j+F(xa2j-xa3j)

(2)

这里的F是放缩因子，hij是新产生的变异个体.

(3)交叉操作

交叉操作是增加种群的多样性，操作如下：

vij(g+1)=

(3)

式中的CR为交叉概率，取[0,1]之间的数；rand(0,1)是[0,1]上服从均匀分布的随机数；randint(1,1,n)是(1,n)之间的一个随机整数；n是个体维数，这种交叉策略可以保证vij(g+1)中至少有一个分量由hij(g)提供.

(4)选择操作

通过调用适应度函数对向量vij(g+1)和向量xij(g)进行比较，作出选择，如公式(4).

(4)

这里的f(·)为调用的适应度函数.

1.2 差分进化算法控制策略

Rainer Storn和Kenneth Price针对差分进化算法还提出了多种控制策略[4,6]，通式表示为DE/x/y，这里：

DE：表示差分进化算法；

x：表示限定当前被变异的向量是“随机的”还是“最佳的”；

y：表示所利用的差向量的个数.

常见的变异控制策略如表1所示.

表1 常见变异控制策略

xbestj代表第g代中最好的个体，a1,a2,a3,a4是从种群NP随机选择的四个个体，并且a1≠a2≠a3≠a4≠i,i是种群NP中的第i个个体，j表示某个个体的第j维.此文选取的策略是DE/rand/1.

1.3 差分进化算法中的参数选取

要想得到理想的结果，参数的选择很重要，差分进化算法中涉及到的参数主要有群体规模NP，放缩因子F，交叉概率CR，个体维数n.NP一般介于5n与10n之间，但不能少于4，否则无法进行变异操作；F一般在(0,2)之间选择；CR只在[0,1]之间选择，CR增大后收敛速度会加快，但容易发生早熟现象；n视实际问题而定.

以上参数的选取只是经验上的选择，对于具体问题，还要进一步研究确定.

2 改进的差分算法对PID参数的优化

2.1 PID参数的优化设置

PID控制器作为一种线性的控制，通过给定的输入与实际输出构成控制偏差，然后求取偏差的比例、微分、积分，再进行线性组合，作为被控对象的输入，其一般表达式为：

式中Kp、Ki、Kd分别表示比例系数、微分系数和积分系数.PID参数优化的目的就是通过优化这三个参数，以期得到最佳控制参数，在满足系统稳定的前提下，保证控制系统的某种性能最佳.

2.2 改进差分进化算法

对于标准的差分进化算法，在变异操作中，放缩因子F，通常是选取一个固定的参数来参与变异.这种选择，表现不出在每次迭代中对变异及后面的交叉、选择操作的影响.又由于种群在进化的早期具有多样性，放缩因子F宜取大一些；在进化的后期应集中搜索，F宜取小一些[7].基于上述思想，标准差分进化算法在变异操作时，对放缩因子F，进行自适应调整，在此选取三种自适应函数：凹函数、线性函数和凸函数，分别对放缩因子F进行自调整[4,5,8,9].

(1)凹函数

选取的凹函数为指数函数：

(5)

记作F1-DE，C是一个常数，这里取为20.

(2)线性函数

线性函数选取为一次函数：

(6)

记作F2-DE.

(3)凸函数

凸函数选取为开口向下的二次函数：

(7)

记作F3-DE.

标准的差分进化算法记作F0-DE.上述各函数中的Fmax和Fmin分别表示放缩因子F的最大值和最小值，t和Tmax分别表示当前迭代次数和最大迭代次数.

2.3 基于改进的差分进化算法的PID优化方法设计

这里以待优化的PID控制参数Kp，Ki，Kd为分量构成一个三维行向量.即组成差分进化算法的个体.参数搜索范围是根据Z-N法获得的参数，向两边扩展选取.以最大迭代次数为终止条件.以常用的系统性能指标函数ITAE，即时间和绝对误差的乘积积分作为适应度函数，其公式如下，ts为调节时间.

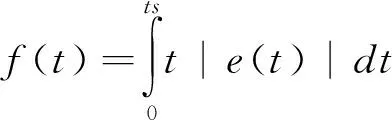
则改进后的算法流程如下：

(1)对PID控制参数Kp、Ki、Kd进行实数编码，设计种群个体，以Z-N法获得的参数，设计搜索空间，根据性能指标要求，设计适应度函数，选择控制策略；

(2)对差分进化算法进行参数设置，包括种群规模NP，放缩因子F的最大值Fmax，最小值Fmin，交叉因子CR，最大迭代次数Tmax；

(3)随机产生初始化种群；

(4)利用公式(5)或(6)或(7)调整放缩因子，根据公式(2)，采用DE/rand/1控制策略进行变异操作；

(5)根据公式(3)进行交叉操作；

(6)根据公式(4)进行选择操作；

(7)判断是否到达最大迭代次数，没有，转至(4)，已达到，则执行(8)；

(8)输出最优结果.

3 改进的差分进化算法优化参数的仿真和比较

以某二阶系统为控制对象进行仿真研究，其传递函数为：

改进的差分进化算法参数选取：种群规模NP取为40；放缩因子F采用公式(5)、(6)或(7)的自调整公式；交叉概率CR取为0.1；个体维数n取为3；最大迭代次数Tmax取为200.

根据文献[6]的研究，考虑到放缩因子的取值范围为(0,2)以及收敛效果，这里最大放缩因子Fmax取为1.90，最小放缩因子Fmax取为0.40.

标准的差分进化算法参数选取，放缩因子F取为0.4，其他参数与改进的差分进化算法的一致.优化参数的取值范围:Kp为[0,40]，Ki为[0,20]，Kd为[0,2].在这里还选取一组非差分进化算法获得的常规参数，根据文献[4]的理论设计方法，取Kp为3.98，Ki为6.78，Kp为4.26.根据差分进化流程，编程仿真，所得仿真图如图1，图2所示.

图1显示的是标准差分进化算法与常规算法的仿真输出曲线；图2显示的是不同放缩因子下的仿真输出曲线.

图1 常规算法与标准DE算法的仿真输出

由图1可知，差分进化算法对PID参数的优化效果要好于常规算法.响应速率要快于常规算法，有效的减小了超调量和调节时间，过渡过程相对比较平滑.

由图2可知，在不同放缩因子的调节作用下，所得不同的优化参数组合，相对于F0-DE而言，三种改进的DE算法作用效果均要优于F0-DE，其中F1-DE速率快，过渡时间短，鲁棒性最好；F2-DE和F3-DE的作用效果次之，响应速率较快，具有一定的超调量，调节过程出现了轻微震荡，鲁棒性较好；而F0-DE效果最差，超调量最大，调节过程出现了明显的震荡，鲁棒性差.

图2 不同放缩因子下的仿真输出

4 结束语

对标准差分进化算法中的放缩因子F，引入三种不同类型的函数对其进行自适应调整，将各自获得的一组最优参数，作为PID的控制参数，作用于被控对象，所得到的仿真图显示，不管是标准的DE算法还是改进的DE算法都要优于常规的算法；在改进的DE算法中采用指数函数优化的F效果最好，响应速率快，鲁棒性好.采用线性函数和凹函数优化的F响应速率和过渡过程大致相当，差异不是很大.差分进化算法能克服传统算法不能寻优的缺点，而改进的差分进化算法具有的自调整特点，能自调整放缩因子，是标准DE算法所不能做到的，因此能满足一定的需求，有一定的参考意义.

[1] Storn R,Price K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997(11)：341-359.

[2] 刘 波，王 凌，金以慧.差分进化算法研究进展[J].控制与决策，2007，22(7)：722-729.

[3] 姜立强，刘光斌，郭 静.基于差分进化算法的PID参数整定[J].计算机仿真，2009，26(6)：204-206.

[4] 唐德翠，朱学峰.改进差分进化PID参数优化及其在凝絮中的应用[J].计算机工程与应用，2009，45(24)：204-206.

[5] Wu Lianghong,Wang Yaonan,Zhou Shaowu,et al.Design of PID controller with incomplete derivation based on differential evolution algorithm[J].Journal of Systems Engineering and Electronics，2008，19(3)：578-583.

[6] Soliman.O.S,Bui.L.T.A self-adaptive strategy for controlling parameters in differential evolution[C]//2008 IEEE World Congress on Evolutionary Computation.Hong Kong: IEEE Conference Publications，2008：2 837-2 842.

[7] 刘广明.差分进化算法及其改进[J].系统工程，2005，23(2)：108-111.

[8] 常俊林，李亚朋，马小平，等.基于改进差分进化算法的PID优化设计[J].控制工程，2010，17(6)：807-810.

[9] 陈贵敏，贾建援，韩 琪.粒子群优化算法的惯性权值递减策略研究[J].西安交通大学学报，2006，40(1)：53-56.