大跨度桁架节点空间位置的测定技术

徐进军，罗喻真，王海城，2，刘卫平

(1.武汉大学精密工程与工业测量国家测绘地理信息局重点实验室，湖北武汉 430079；2.河北水利水电勘察设计研究院，天津 300250；3.中建三局工程总承包公司，湖北武汉 430064)

大跨度桁架节点空间位置的测定技术

徐进军1，罗喻真1，王海城1，2，刘卫平3

(1.武汉大学精密工程与工业测量国家测绘地理信息局重点实验室，湖北武汉 430079；2.河北水利水电勘察设计研究院，天津 300250；3.中建三局工程总承包公司，湖北武汉 430064)

大跨度钢结构桁架的高精度安装定位是实际工程中经常面临的问题。本文针对大跨度钢结构体的特点，研究了采用无接触测量的方式确定桁架杆件节点空间位置的理论与方法，推导了计算公式。实际试验结果计算表明其在数据获取和处理上具有实用性、准确性和高效性。

大跨度；圆管；节点；空间位置；无接触测量

一、概 述

近20余年来，由于采用了许多新材料和新技术，各种类型的大跨度空间结构发展很快，大屋盖跨度超过150 m以上的超大规模建筑已非个别。在我国相继出现了一批具有代表性的新型空间钢结构，如2000年建成的广州新体育馆采用的是跨径为160 m的拱-桁架-椭圆圈梁结构[1]；2003年建成的广州会展中心采用的是跨径为126 m的张弦桁架结构[2]；北京国家大剧院，其东西跨度为212.24 m，南北跨度为143.64 m[3]。

大跨度张弦桁架是近几年在我国迅速发展起来的一种新型钢管结构。由钢管直接焊接而成的管节点承载着整个屋顶的静、动力载。由于影响管节点的因素众多，刚度难以描述，为此，安装质量的控制非常重要。在某一阶段安装竣工后，如何检验各个杆件和节点是否安装到位，与设计值相差多少，变形量多大，这些问题直接事关今后的安全运营。

目前，对这类结构的检测较多采用了全站仪的接触测量法[2-4]，即测量时，需要事先在构件的目标点上安置反射片或做标记。但标记容易被破坏，安置反射片或棱镜测量效率低、危险性大，特别是在竣工卸除脚手架后，人员难以到达高空测量点。地面三维激光扫描是一种无接触测量技术，对于整体形状的测量或异型形状测量有其独特的优势，但后期处理点云数据的工作相对复杂[5-6]。如果进行杆件抽检，地面三维激光扫描的测量效率并不高[7-8]，因此，利用全站仪免棱镜测量技术与相应的数据处理理论对节点的实际空间位置进行测定，具有重要的实用价值。

二、节点中心确定技术与方法

对于杆件相交处的节点，一般有两类形式：①杆件集结于一个圆球，如图1(a)所示；②杆件“直接”相交，如图1(b)所示。目前已有多款全站仪，不仅具有高精度的角度测量功能，而且具有高精度的免棱镜测距功能。这些现代测量仪器的技术革新，为问题的解决提供了条件。

图1 节点两种结构形式

1.球形节点

当节点处是球体时，首先建立一个整体坐标系；然后在不同方位设站，对中、整平、定向后，尽可能多地从不同测站测量球体表面点三维坐标；最后采用球体拟合的方法计算球心坐标。为了提高球心解算精度，可采用整体最小二乘法[9]，即所有测点到拟合球球面的距离平方和最小。

2.相交节点的确定

当杆件相交点结合处没有明显规则形状时，就需要通过轴线相交计算节点的坐标。相交于节点的杆件可以是空间直线或空间曲线。结合实际情况且不失一般性，这里讨论空间曲线相交，而且本文说的空间曲线是指位于某个空间平面上的曲线。

(1)圆管杆件轴线确定

图2表示3条空间曲线的空间关系。3条曲线分别位于平面P1、P2、P3上。由于制造、安装、测量误差的存在，3条曲线在空间不会相交于一点。对于实际的圆管工程杆件，空间曲线就是杆件的轴线，因此，首先必须获取位于轴线上的一些点的坐标。

采用免棱镜全站仪，根据杆件的空间姿态，对杆件的不同部位进行横扫、竖扫，获得圆管杆件表面测量点，这些点是椭圆(或圆)线。对该椭圆线进行拟合，得到扫描部位的轴线点三维坐标，具体详见文献[8]。对一个杆件的多个部位扫描，可得到轴线上多个点，由这些点构成杆件轴线。

图2 曲线空间关系

(2)平面曲线方程的获取

实际测量时仪器都要整平，因此，测量坐标系的X轴水平，Z轴铅直，并构成右手坐标系。但对于测量得到的轴线上的离散点是三维点，不容易直接进行曲线拟合，需要变换到测量点所在的平面，即降至二维才能方便拟合。具体过程如下：

1)确定测点所在平面(如图3的P1平面)：根据轴线上测量点的三维坐标，采用最小二乘拟合的平面必然通过测量点的重心XTS＝(xs，ys，zs)。因此，不妨定义拟合的平面方程为

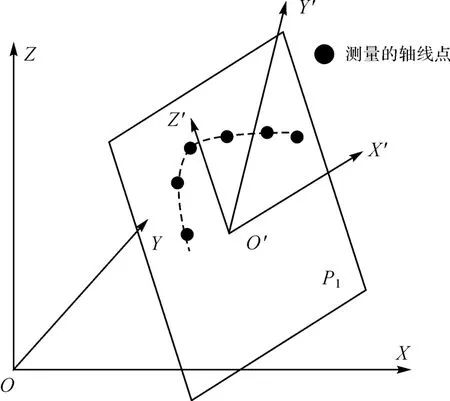
图3 曲线空间拟合与表达

2)定义拟合曲线的坐标系：为了便于曲线的拟合和表述，在P1上定义坐标系O′X′Y′Z′。其中，O′为所有测点重心；X′轴过O′且平行于P1与XOY平面的交线。Y′过O′且平行于平面法向量(向上)，右手法则确定Z′轴。

3)坐标变换：要实现OXYZ到O′X′Y′Z′两个坐标系的转换，需要先将原点移至重心，再进行旋转变换。为此，根据O′X′Y′Z′的定义，可以确定O′X′、O′Y′和O′Z′3个坐标轴在OXYZ中的方向向量为

4)平面曲线拟合：根据式(5)将测量点坐标转换到P1平面上，变换后各点的y′值理论上应该等于0(由于实际测量误差的存在，其实际值都接近于0，这也可以作为变换是否正确或测量点是否含有粗差的检验条件)。这样，通过变换将三维降至二维，非常便于平面曲线的拟合。

出于通用性和实际情况，选定拟合曲线为一元二次多项式

在进行平面曲线拟合时，同样采用整体最小二乘拟合原则[10](如图4所示)，得到误差方程式为式中，li＝a0＋a1x′i＋a2x-z′i。换成矩阵形式及未知数的解同式(3)。

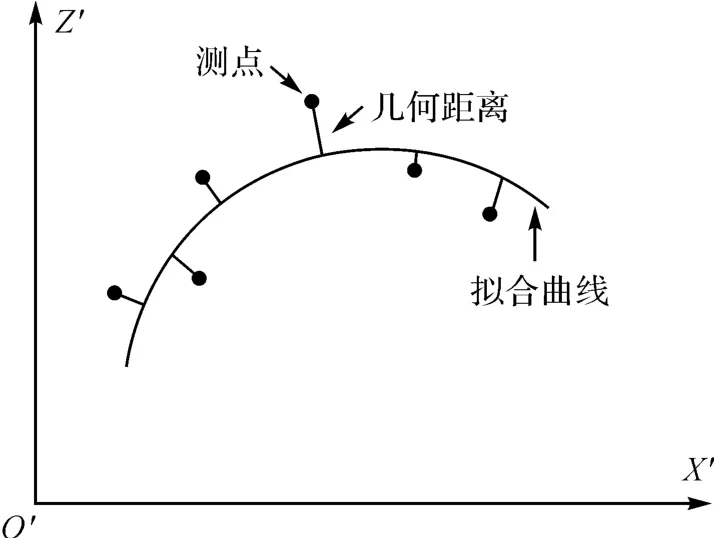
图4 平面曲线拟合

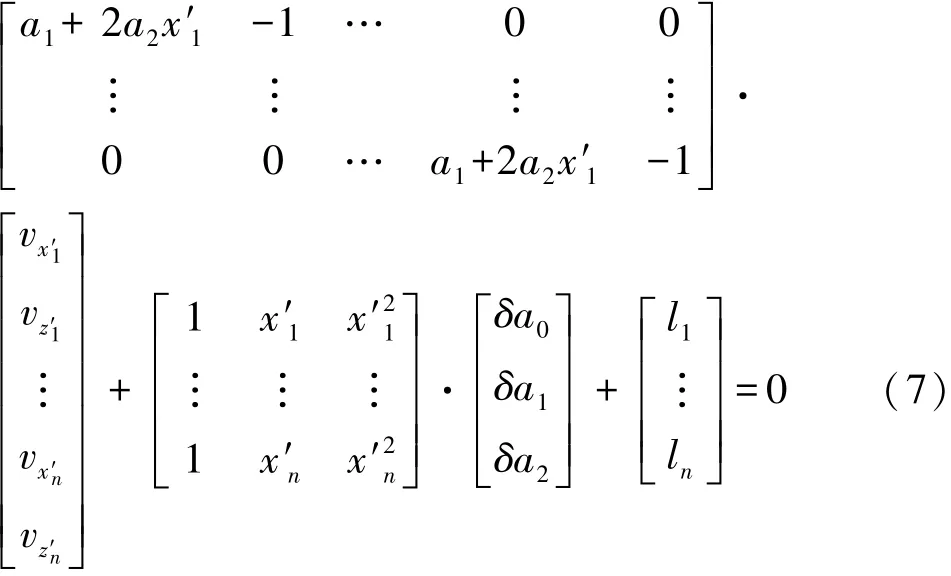
(3)平面曲线方程的空间表示

经过本节第(1)段的数据处理后，得到了各个轴线在各自所在平面的曲线方程(6)。为了计算这些曲线的空间交点，还需要将这些曲线方程转回到统一的测量坐标系中。以P1平面为例，按照式(5)进行逆变换，可得到该曲线在测量坐标系下的空间函数表达式(采用参数表示)为

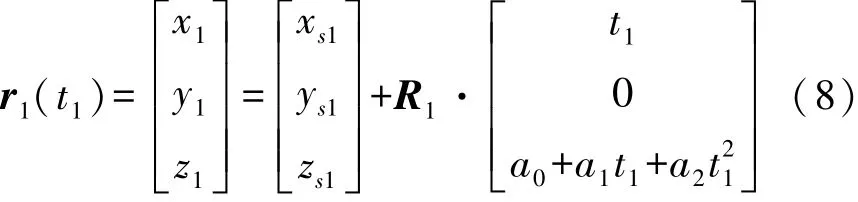
同样的过程可以得到如式(8)的其他轴曲线的空间函数表达式r2(t2)、r3(t3)等。

(4)空间曲线交点确定

由于测量误差、制造误差及安装误差的存在，这些曲线在空间是异面的，不会相交于同一点。为此，定义如图5所示的两条空间异面曲线的交点是位于两曲线之间的最短距离[11]的中点。

图5 两条异面曲线“交点”

限于篇幅，具体表达式不再展开。式(9)由含两个未知数t1、t2的两个非线性方程组成，采用Newton-Raphson迭代计算方法解算出未知数t1、t2，代入式(8)即得两垂足点的坐标，两点取平均得到最短距离中点的坐标，该迭代算法需要较好的近似值。在实际工程中，近似值可由仪器直接测量交点附近点获得，非常容易。

(5)节点坐标确定

为了更好地消除误差，提高精度和可靠性，一般计算节点坐标时，需要测量过节点的3条或4条杆件轴曲线。而且选择的轴曲线能构成较好的交会角度，如同经纬仪多点前方交会原理一样。以图6所示的3条轴曲线求节点坐标为例，根据本节第(3)段的方法，可求得两两曲线的“交点”，这样就得到3个空间点(x1，y1，z1)、(x2，y2，z2)、(x3，y3，z3)。这3点的重心点即可认为是3条轴曲线的空间交点(x，y，z)，也就是杆件节点的坐标。

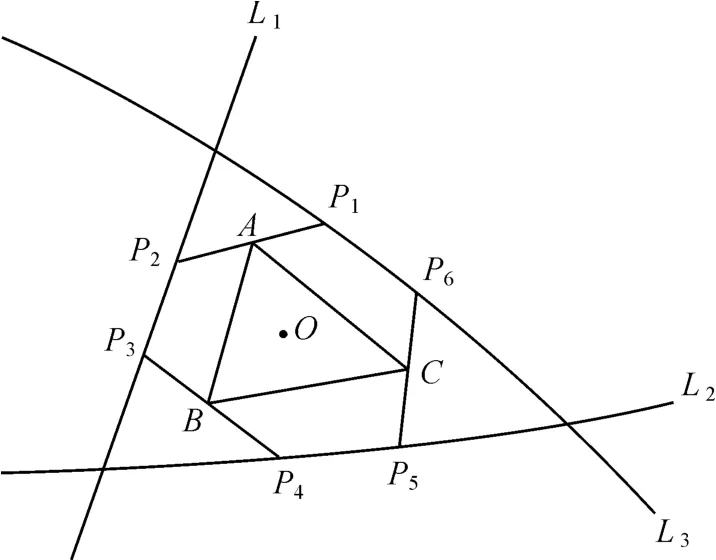
图6 多条异面曲线最佳交点位置

三、试验数据分析

1.球形节点计算试验

在室内对图7(a)所示的球，采用徕卡1201 TCRA以前方角度交会的方式(视线切球体的上、下、左、右边沿取平均)确定出两球心的坐标。同时，在两个测站上测量球表面若干点，并拟合出球心坐标。两种方法的结果一致(见表1)。

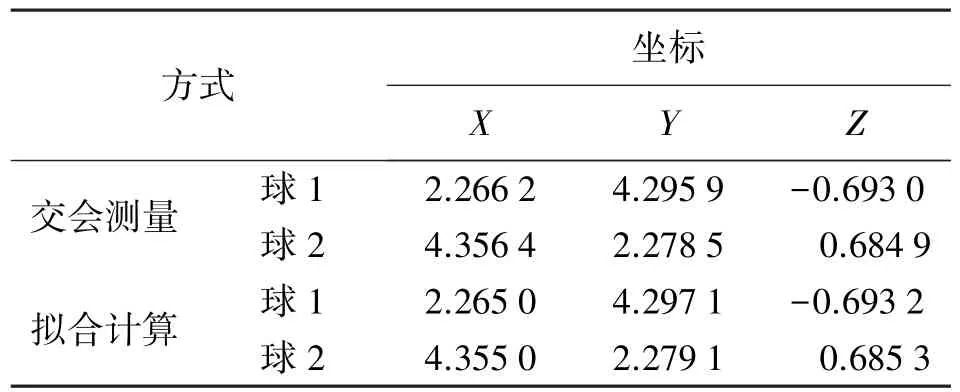
表1 球心点的测量坐标比较m

2.相交节点试验

在室内利用两根直径39 cm的塑料管，使其表面相交，如图7(b)所示。采用徕卡1201 TCRA对每根管的表面扫描测量8个椭圆截面，并计算出16个椭圆截面中心轴线点坐标，结果见表2。

按照以上方法和步骤，计算出两管间最短距离的垂足坐标为(100.481，101.128，10.379)、(100.733，101.186，10.091)。两点之间的距离为0.387 m，正好等于管直径，与实际管径相吻合，验证了上述研究的理论与方法的正确性。最后得到空间相“交点”坐标为(100.607，101.157，10.235)。

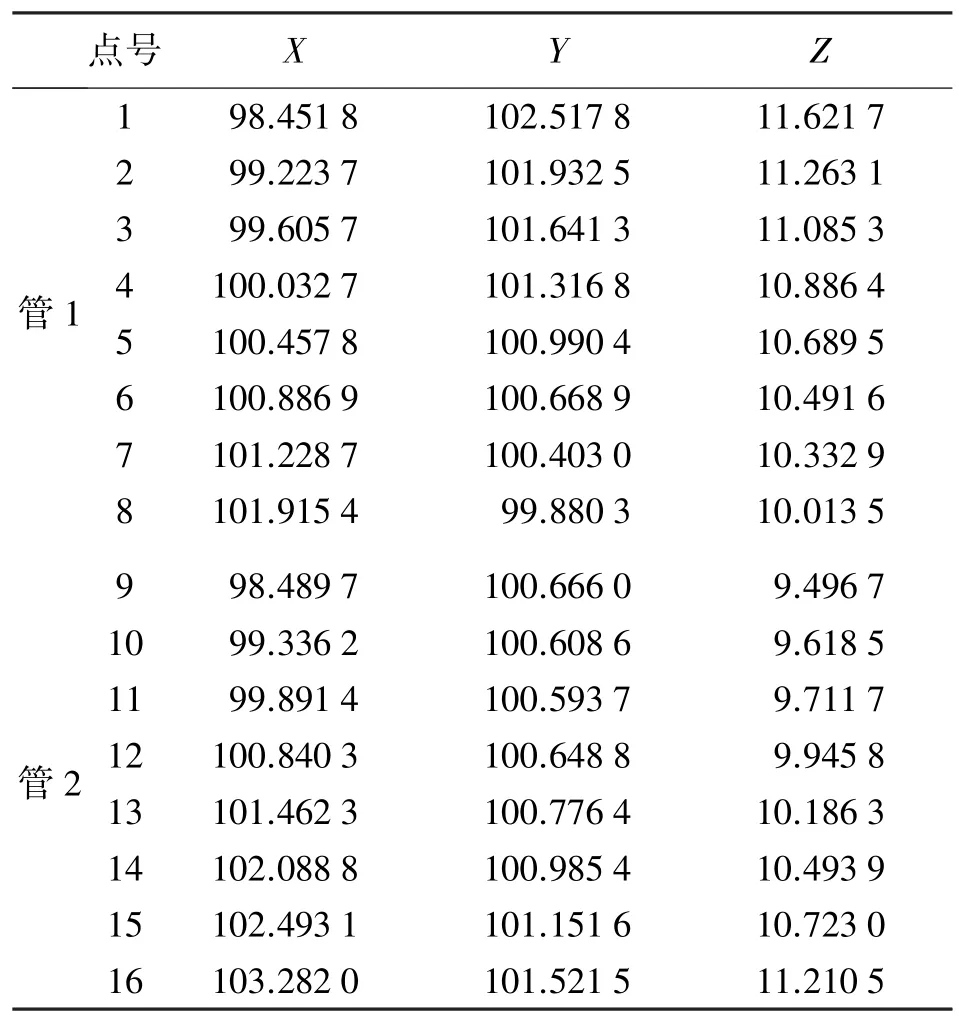
表2 轴线点测量坐标m

图7 测量试验

四、结束语

通过室内实际试验测量，验证了采用全站仪无接触测量方式获取大跨度空间节点位置的有效性和高效性。既能满足大型场馆检测精度要求，又大大节约了成本，提高了作业效率和保障了作业安全。该方法既可以用于场馆杆件安装前后的定位检测，也可以进行变形监测。

本文主要讨论了圆管形的杆件相交节点和球体节点的确定问题。对于其他形状的杆件(如矩形截面、工字形等)，如果能够通过测量手段获得轴线，同样可以采用本文的思路加以解决。对于多条空间异面曲线最佳交点的确定，不同的准则下，结果肯定会有所区别。一般而言，这种相差应该很小。

[1] 曾慧敏.广州新体育馆钢屋架施工质量控制[J].广东土木与建筑，2001(9)：37-39.

[2] 邓晖，朱建军.大跨度张弦桁架变形监测研究[J].工程勘察，2005(3)：56-58.

[3] 秦长利.国家大剧院施工测量方法与实践[J].测绘通报，2006(8)：69-70.

[4] 李锦城.大跨度钢结构屋架挠度变形监测方法[J].铁道建筑，2006(12)：96-98.

[5] 周克勤，吴志群.三维激光扫描技术在特异型建筑构件检测中的应用探讨[J].测绘通报，2011(8)：42-44.

[6] 王晏民，王国利.激光雷达国家体育馆屋顶钢结构安装滑移质量监测[J].工程勘察，2009(12)：17-21.

[7] 赵群，刘键，陈金科.应用激光扫描法对国家体育馆大跨度钢屋架滑移过程变形监测与分析[J].测绘科学，2007，32(3)：110-111.

[8] 徐进军，王海成，罗喻真，等.圆管轴线点测量方法研究[J].大地测量与地球动力学，2011，31(1)：49-54.

[9] 鲁铁定，周世健，张立亭，等.基于整体最小二乘的地面激光扫描标靶球定位方法[J].大地测量与地球动力学，2009，29(4)：102-105.

[10] 丁克良，欧吉坤，赵春梅.正交最小二乘曲线拟合法[J].测绘科学，2007，32(3)：17-19.

[11] 马广韬.基于Mathematica的异面曲线最短距离的优化计算[J].机械设计与制造，2005(6)：27-28.

Measuring Technology of Spatial Position of Node for Truss Structures with Large-span

XU Jinjun，LUO Yuzhen，WANG Haicheng，LIU Weiping

P258

B

0494-0911(2014)09-0047-04

2013-07-06

国家自然科学基金(41274021)

徐进军(1966—)，男，湖北天门人，教授，研究方向为精密工程测量。引文格式:徐进军，罗喻真，王海城，等.大跨度桁架节点空间位置的测定技术[J].测绘通报，2014(9)：47-50.

10.13474/j.cnki.11-2246. 2014.0291