北斗非GEO卫星信号码并行捕获

许良备，应忍冬，陈 新，刘佩林，赵 毅

(1.上海交通大学，上海 200240；2.上海华测导航技术有限公司，上海 200233)

北斗非GEO卫星信号码并行捕获

许良备1，应忍冬1，陈 新1，刘佩林1，赵 毅2

(1.上海交通大学，上海 200240；2.上海华测导航技术有限公司，上海 200233)

2012年12月，北斗二代的接口控制文件正式公布。北斗B1I频点的非GEO卫星上调制20 bit的NH码，因此每1 ms信号可能存在比特跳变。借鉴传统GPS并行码相位捕获算法，本文研究了一种基于补零FFT的并行码相位算法。该算法能够实现1～20 ms相干积分，利用非相干累加提高信噪比，并采用一种对信号强度和采样率不敏感的判决变量。仿真表明，通过相干积分和非相干累加，该算法使用400 ms数据可以捕获24 dBHz的弱信号。

北斗二代；捕获；信噪比；快速傅里叶变换

一、引 言

全球卫星导航系统(global navigation satellites systems，GNSS)已进入一个新的发展阶段。除了进入现代化计划的GPS，中国的北斗二代也进入了实用化的关键阶段。2012年12月，北斗二代的接口控制文件正式公布。

对于GNSS信号的处理主要包括捕获、跟踪及解算。其中捕获阶段因为需要卫星信号进行三维搜索，计算资源消耗大，其灵敏度相比跟踪阶段低，是制约GNSS定位在弱信号应用的瓶颈。目前常用的搜索策略有串行搜索[1-2]、频率并行搜索[3]、码并行搜索[4]策略。频率并行搜索和码并行搜索利用快速傅里叶算法提高运算效率，加快捕获速度，从而能够在一定时间内捕获到更弱的信号。

通常处理一个扩频码周期获得的信噪比增益不足以捕获弱信号(如低于44 dBHz的GPS L1信号)。因此需要对多个周期的结果进行累积，提高处理增益。常用的累积方法有：相干积分累加、非相干积分累加、差分相干积分累加[5]。文献[6]详细比较了3种累加方式的性能，相干积分累加对信噪比的提升最大，同时需要减小频率搜索步长；非相干积分累加引入了平方损耗，但是无须减小频率搜索步长；差分相干积分累加的信噪比增益介于两者之间，同时无需减小频率搜索步长，但是算法比较复杂。文献[7]提出了半比特交替法及估计比特跳变的全比特方法，该方法在10 ms或20 ms相干积分，总信号长度30 s基础上，利用码并行搜索算法可以捕获到14 dBHz。

上述方案在理论情况下能够捕获足够弱的信号，而只受限于接收机、卫星动态及计算能力。因为高灵敏度捕获要求在短时间内消耗巨大的计算资源，因此有许多研究者提出了各种优化算法。文献[8]在半比特交替法及估计比特跳变的全比特方法基础上提出了1/4字节步进法，该方案能够用更短信号长度捕获到相同灵敏度的弱信号。另外文献[9]利用延时相关法，将多普勒和码相位的二维搜索变成两个一维搜索过程，从而提高捕获速度，不过该算法增加了噪声功率，并不适用弱信号捕获。文献[10]利用数学运算技巧减少码并行捕获算法冗余计算量，从而提高捕获效率。文献[11]则从整体捕获策略上对捕获过程进行优化，提高捕获速度。

北斗B1I信号是2012年12月公布的最新北斗二代导航信号。北斗GEO卫星播发D2电文，其码率为500 bps；非GEO卫星播发D1电文，其码率为50 bps，另外调制20比特码率为1 Kbps的二级码(NH码)。北斗非GEO卫星的信号结构与传统GPS L1信号有较大区别，因此需要新型优化捕获算法。文献[12]提出了一种双通道捕获算法，不过目前北斗只公开I路信号结构，因此该算法还未能在实际信号中使用。文献[13]提出一种导航比特边沿、多普勒、码相位联合搜索算法，不过该算法运算量大，并且相干积分时间只能取1 ms和20 ms，难以适应强弱不同信号的捕获。

为此本文根据北斗B1I非GEO卫星信号结构特点研究一种可变相干积分时间的捕获算法。该算法利用补零后的FFT完成部分NH码周期的循环卷积运算，并利用非相干累加提高信噪比，从而捕获弱信号。

二、北斗卫星信号结构

北斗B1I信号结构在文献[1]中公开。其中非GEO卫星信号结构如图1所示。

图1 北斗B1I非GEO卫星信号结构

其信号可以表示为

式中，j表示卫星编号；A表示信号振幅；N表示二级码；C表示测距码(扩频码)；D表示测距码上面调制的数据码；f0是载波频率；φ是载波初始相位。因为捕获过程对于每颗卫星都是一样的，因此下面省略卫星编号j。

相比较GPS L1信号，北斗B1I非GEO卫星信号除了扩频码率、载波频率及导航电文比特率不一样外，其信号还调制20比特的二级码。该二级码是Neumann-Hoffman码(NH码)，其1比特宽度与扩频码周期相同，20比特排列如下(0 0 0 0 0 1 0 0 1 1 0 1 0 1 0 0 1 1 1 0)。

三、北斗非GEO卫星捕获

1.基于FFT的码并行捕获算法

码并行捕获算法首先应用于GPS L1信号捕获[6]。该算法对N ms(1≤N≤10，N为整数)的数据下变频后变换到频率域，本地产生N ms扩频码，变换到频率后取共轭，二者相乘并取IFFT转换到时域，获得接收信号与本地扩频码的卷积结果，最后进行M次非相干累加，从而快速捕获弱信号。对于B1I上非GEO卫星信号，因为其调制有1 Kbps的NH码，因此N并不能取任意值，因为NH码会使相邻毫秒的数据极性相反，从而抵消扩频增益。

为此利用补零FFT解决NH码带来的跳变问题。例如要实现N ms(1≤N≤20，N为整数)相干积分可以采用如下策略。假设搜索载波频率频点为fk(k＝0，1，…，K)，具体步骤如下：

1)将输入信号与频率fk的载波相乘下变频至基带信号。

2)将输入信号2N ms一段分为L段，N (L＋1)＞20，每相邻两段信号有N ms的重合，这样共N( L＋1)ms信号，记为si[n](i＝0，1，…，L-1)。本地产生N ms的扩频码信号，调制上N比特的NH码，如前N个比特(0 0 0 0…)，本地信号补零至2N ms，记为c[n]。

3)利用FFT算法分别将L段2N ms输入信号转换到频域，得到Si[n]＝FFT(si[n])，i＝0，1，…，L -1。

4)利用FFT算法将本地2N ms信号转换到频域，并取共轭

5)将频域的本地信号与频域的输入信号相乘并取IFFT转换到时域，得到本地信号与输入信号的卷积Ri[n]＝IFFT(C[n]·Si[n])，i＝0，1，…，L-1。

6)搜索下一载波频点fk＋1，重复步骤1)—5)，得到L个二维矩阵Ri(i＝0，1，…，L-1)。

7)因为N( L＋1)＞20，因此至少存在一段2N ms信号i，含有一段N ms信号，其NH码与本地产生的NH码对齐。当该卫星可见，并且扩频码相位对齐和多普勒频点对齐，能够在Ri得到一个峰值，从而捕获到该卫星信号(如图2所示)。

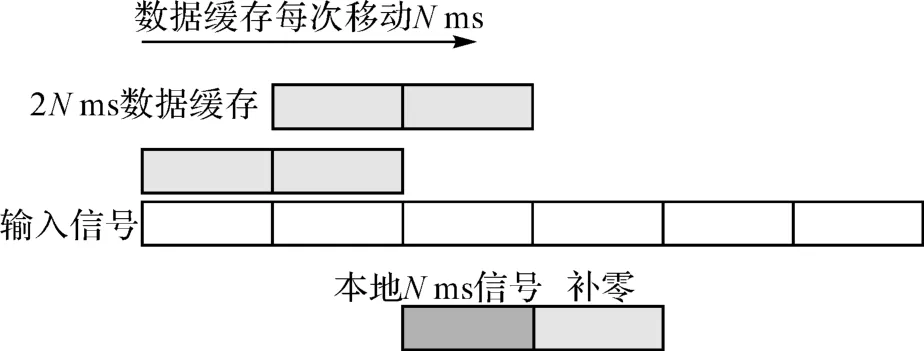
图2 N ms相干积分示意图

2.非相干累加

因为未知导航比特边沿跳变的影响，上述算法最多只能实现20 ms的相干积分累加。为了捕获到更弱的信号(如信号功率小于34 dBHz)，需要非相干累加，进一步提高信噪比。非相干累加是对相关结果取模后进行二次累加的过程，其数学原理如下

在前面的N ms相干积分基础上，利用非相干累加，可以不用缩短频率搜索步长，获得一定的信噪比增益，从而快速捕获弱信号。同时需要注意的一点是，该方法引入了“平方损耗(squaring loss)”，使得其信噪比改善效果降低。图3给出了一定次数的非相干累加次数下的信噪比增益。

图3 非相干累加次数与非相干增益

3.判决变量

非相干累加后得到L个二维矩阵矩阵的每个元素对应一个多普勒频点和扩频码相位组合。为了适应信号强度的变化及采样率的变化，增强判决算法鲁棒性，采用如下判决变量

式中，ymax是L个二维矩阵的最大值；ymean是二维矩阵的近似方差。

实际上无须遍历Yi，NC的所有元素计算其近似方差，而是简单遍历足够数量的元素即可，如1000个元素。当D大于预设定的阈值则宣布捕获成功。

四、仿真和测试结果

在Matlab中实现仿真，利用Matlab产生B1I非GEO卫星信号，共产生强、中、弱3种强度的信号，并对该算法进行测试验证。信号参数为：卫星编号sv＝6，中频IF＝2.42 MHz，多普勒频移DP＝2345 Hz，初始码相位CP＝100 Chip，采样频率FS＝12.288 MHz，噪声功率密度N0＝204 dBW/Hz，信号强度C/N0＝44 dBHz、34 dBHz、24 dBHz。捕获结果分别显示在图4—图6。从图中可以看出，当码相位对齐时，相关值出现较明显的尖峰，该算法对强、中、弱3种信号均能成功捕获。

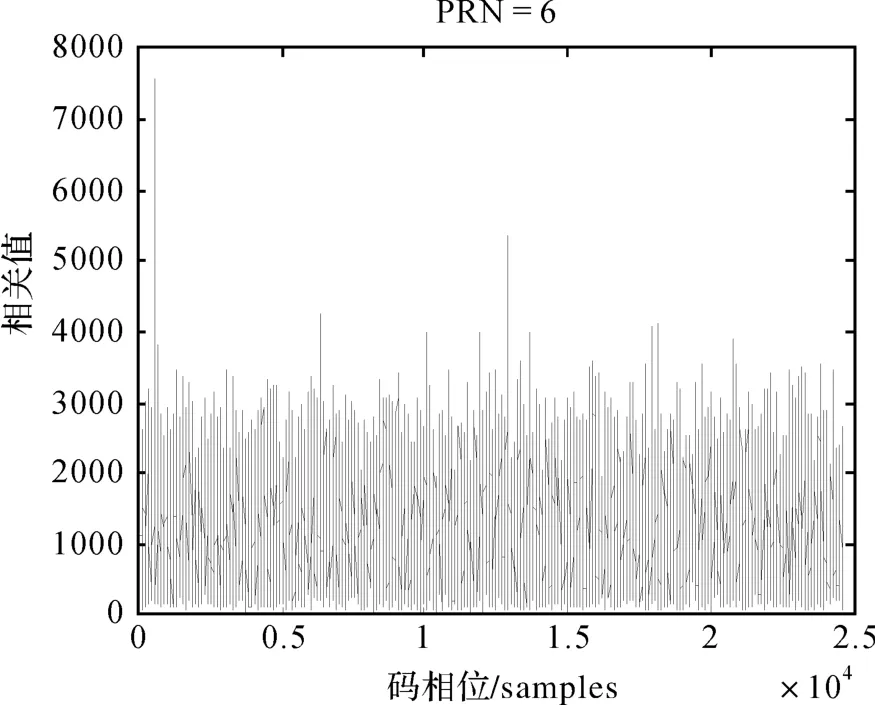
图4 C/N0＝44 dBHz捕获结果

图5 C/N0＝34 dBHz捕获结果

图6 C/N0＝24 dBHz捕获结果

从表1可以看出，码片误差值0.3码片以内，而多普勒误差与频率搜索步长有关，相干积分时间增长，搜索步长减小，多普勒误差也减小。对于强弱不同的信号，通过配置相干积分时间和非相干累加次数可以在捕获速度和灵敏度方面取得好的折中。如强信号44 dBHz时，1 ms相干积分和1次非相干累加即可快速捕获信号。而要捕获24 dBHz的弱信号，则需要20 ms的相干积分和20次非相干累加次数，这种情况下捕获运算量是巨大的。为了减小捕获运算量，可以采用10ms相干积分和更多次的非相干累加次数，同时也能扩大频率搜索步长，从而降低一定运算量。另外需要指出的是，因为平方损耗的原因，无限次增加非相干累加次数并不能获得足够的信噪比增益从而捕获弱信号。如图3所示，非相干次数从100增加到1000，其信噪比增益不到5 dB。

表1 北斗6号卫星捕获结果

致谢:本工作受到了上海市北斗导航与位置服务重点实验室和上海华测导航技术有限公司的资助，在此一并感谢。

[1] 谢钢.GPS原理与接收机设计[M].北京：电子工业出版社，2009：366-368.

[2] KAPLAN E D，HEGARTY C J.Understanding GPS：Principles and Applications[M].2nd Ed.[S.l.]：Artech House，1996：162-170.

[3] SPANGENBERG S M，SCOTT I，MCLAUGHLIN S，et al.An FFT-based Approach for Fast Acquisition in Spread Spectrum Communication Systems[J].Wireless Personal Communications，2000，13(1-2)：27-55.

[4] VAN NEE D J R，COENEN A.New Fast GPS Code-acquisition Technique Using FFT[J].Electronics Letters，1991，27(2)：158-160.

[5] ELDERS-BOLL H，DETTMAR U.Efficient Differentially Coherent Code/Doppler Acquisition of Weak GPS Signals[C]∥2004 IEEE Eighth International Symposium on Spread Spectrum Techniques and Applications.[S. l.]：IEEE，2004：731-735.

[6] BORIO D，O’DRISCOLL C，LACHAPELLE G.Coherent，Noncoherent and Differentially Coherent Combining Techniques for Acquisition of New Composite GNSS Signals[J].IEEE Transactions on Aerospace and Electronic Systems，2009，45(3)：1227-1240.

[7] PSIAKI M L.Block Acquisition of Weak GPS Signals in a Software Receiver[C]∥ION GPS.Salt Lake City：[s. n.]，2001：1-13.

[8] 张兴新，罗懋康.一种基于FFT块处理的微弱GPS信号检测新方法[J].四川大学学报：自然科学版，2012，49(3)：494-498.

[9] LIN D，TSUI J.Acquisition Schemes for Software GPS Receiver[C]∥Proceedings of ION GPS.[S.l.]：Institute of Navigation，1998：317-326.

[10] AKOPIAN D.Fast FFT Based GPS Satellite Acquisition Methods[J].IEEE Proceedings-Radar，Sonar and Navigation，2005，152(4)：277-286.

[11] CHUANG M Y，FENG K T.Adaptive GPS Acquisition Technique in Weak Signal Environment[C]∥Vehicular Technology Conference，2006.[S.l.]：Spring，2006：2612-2616.

[12] 黄隽祎，李荣冰，王翌，等.北斗B1 QPSK调制信号的高灵敏度捕获算法[J].航空计算技术，2012，42(5)：38-42.

[13] 薛文通.史雅茹，白阳，等一种捕获北斗D1卫星导航系统弱信号的方法：中国，201210412200.9[P]. 2013-02-13.

[14] 刘莉，战兴群，刘卫，等.北斗卫星导航系统和GPS兼容性评估[J].测绘学报，2011，40(S1)：11-18.

Code Parallel Acquisition of BeiDou None-GEO Satellite Signal

XU Liangbei，YING Rendong，CHEN Xin，LIU Peilin，ZHAO Yi

P228.4

B

0494-0911(2014)09-0012-04

2013-07-06

国家863计划(2012AA12A209)；上海市科委科研计划(11511501700)

许良备(1989—)，男，福建泉州人，硕士，主要从事GNSS接收机设计工作。

许良备，应忍冬，陈新，等.北斗非GEO卫星信号码并行捕获[J].测绘通报，2014(9)：12-15.

10.13474/j.cnki.11-2246.2014.0282