BDS/GPS/GLONASS融合定位模型及性能分析

李鹤峰，党亚民，秘金钟，谷守周，张德成

(1.国核电力规划设计研究院，北京 100095；2.中国测绘科学研究院，北京 100830；3.国家测绘地理信息局第一大地测量队，陕西西安 710054)

BDS/GPS/GLONASS融合定位模型及性能分析

李鹤峰1，2，党亚民2，秘金钟2，谷守周2，张德成3

(1.国核电力规划设计研究院，北京 100095；2.中国测绘科学研究院，北京 100830；3.国家测绘地理信息局第一大地测量队，陕西西安 710054)

针对传统GNSS单星座系统定位存在的诸多不足，基于单点定位，给出建立在时空统一上的BDS/GPS/GLONASS多模融合定位模型，并对实测三系统数据分不同方案进行定位解算，分析各方案的可见卫星数、精度衰减因子(DOP)及定位精度。结果表明，BDS/GPS/GLONASS融合系统可见卫星数大幅提高，DOP值显著下降，定位的精度和可靠性优于各单系统。

BDS；GNSS；多频多模；时空统一；融合定位

一、引 言

自GPS问世以来，其在众多领域发挥了无可替代的作用。随着GPS应用范围的扩大和研究的深入，单星座系统如可见星有限、定位精度不高、可靠性不好等诸多弊端浮出水面。GLONASS系统的加入掀起了一轮有关GPS/GLONASS组合定位研究的热潮，并取得了可喜的研究成果[1-3]。随着BDS的不断完善及Galileo计划的实施，国内外学者对组合定位的研究也涉及BDS/GPS、GPS/Galileo等方面[4-6]，而对三系统融合定位方面的研究还处于探索阶段，一方面由于BDS没有完全覆盖全球，Galileo还处于试验阶段；另一方面早期BDS有关数据涉及保密，难以获取，而模拟仿真数据不能很好地契合实际的定位效果。鉴于目前条件成熟，本文在单点定位的基础上，详细研究了基于时空统一的BDS/GPS/GLONASS融合定位模型，并利用三系统接收机实地采集数据，基于Visual C＋＋平台，编写多模融合定位程序，对实测数据分不同方案进行定位解算，分析各方案的卫星数、DOP值及定位精度。结果表明，BDS/GPS/ GLONASS融合系统较各单系统可见卫星数大幅提高，DOP值急剧下降，定位精度和可靠性显著提升。

二、基于时空统一的BDS/GPS/GLONASS融合单点定位模型

BDS/GPS/GLONASS融合定位采用空间距离的后方交会，与单系统定位原理基本相同。唯一有所不同的是融合系统涉及3个导航定位星座，而各星座系统的时间框架和坐标框架互不相同。欲实现系统的融合定位，首先要完成系统间的时空统一。图1为BDS/GPS/GLONASS融合单点定位流程图。

图1 BDS/GPS/GLONASS融合单点定位流程

1.时空统一

BDS时间框架采用起算历元为UTC 2006-01-01T00∶00∶00的北斗时(BDT)，属原子时(AIT)系统，无闰秒，坐标框架采用2000国家大地坐标系(CGCS2000)[7]。GPS时间框架采用起算历元为UTC 1980-01-01T00∶00∶00的GPST，同属于无闰秒的AIT，BDT与GPST图解关系如图2所示，坐标框架采用WGS-84坐标系；GLONASS时间框架与BDS、GPS定义完全不同，其产生基于GLONASS同步中心CS(Central Synchronize)时间，属UTC系统，此外，GLONASST与UTC(SU)存在有3 h的整数差；坐标框架为俄罗斯地面网与空间网联合攻关平差建立的PZ-90坐标系。BDS、GPS、GLONASS三系统的时间和坐标框架相关参数见表1。

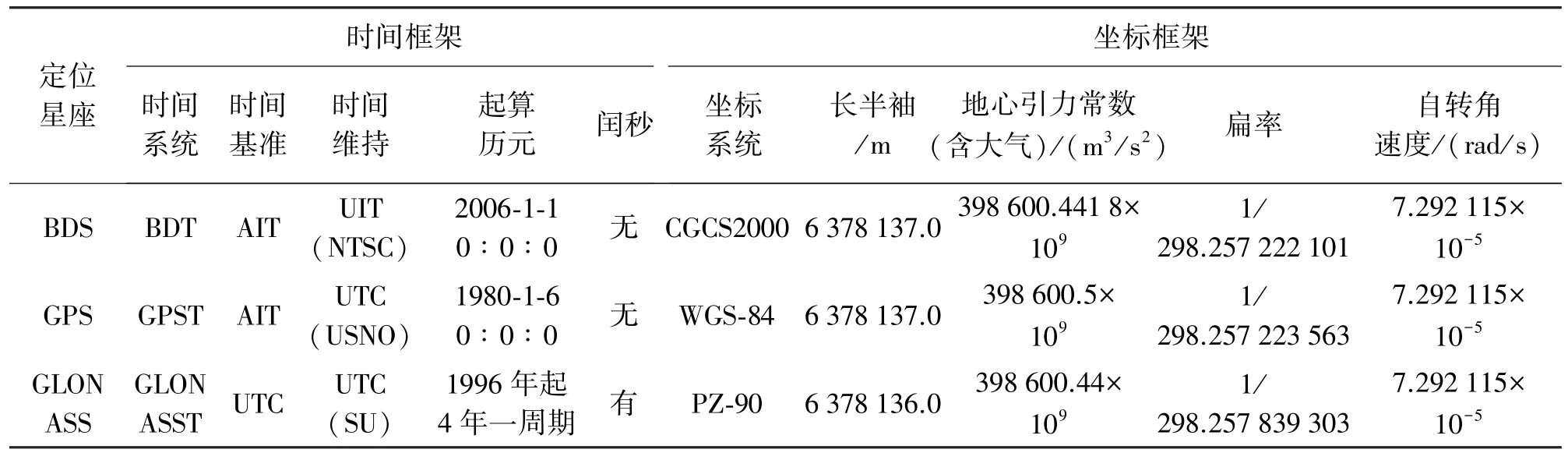
表1 BDS、GPS、GLONASS各系统时间框架和坐标框架参数对比

从表1对比分析可以清晰地看出，BDS、GPS、GLONASS各自的时间和坐标框架互不相同，而融合定位必须建立在同一时空基准上。选取GPST和WGS-84为中间变量，将BDS、GLONASS的时空统一到GPS时空基准下，即三系统融合定位是以GPST为时间框架，得到WGS-84系统下的坐标成果。

借鉴GPS的伪距观测方程[8-9]，可以分别得到BDS、GLONASS的伪距观测方程。假设伪距观测量ρ已通过各项误差(大气延迟、卫星钟差、相对论等)改正，各系统的伪距观测方程可表示为

对于时间的统一，由表1可以得到GPST与 BDT之间的图解关系，如图2所示。

图2 BDT、GPST之间的图解关系

从图中可以清晰地得到GPST与BDST的转换关系

由上文可知，GLONASST与UTC有3 h的整数差，但实际多模接收机接收到的GLONASS导航文件中的参数信息并非建立在GLONASST下，而是UTC。通过文献[6]可得GPST与GLONASS系统的UTCGLO间的转换关系

式中，n为国际UTC与AIT之间的调整参数，截至2013年5月，该调整参数n＝35。然而，由表1可知，GLONASST的起算历元从UTC时1996年起，4年一周期。因此在定位解算时，顾及该条件，判断当前观测时间的起算历元，起算年后的闰秒不予考虑在内，即对于不同年份的观测数据，n的值不尽相同，这一点要非常注意。

在坐标统一方面，PZ-90到WGS-84的转化按MCC得到的目前国际最高精度的布尔萨七参数改正模型进行转化[8]，其七参数改正公式为

由表1可以看出，CGCS2000与WGS-84坐标系的定义几乎一致，魏子卿院士认为CGCS2000和WGS-84是相容的，在坐标系实现精度范围内，CGCS2000和WGS-84是一致的[10]。所以在实际GNSS融合定位中，二者无须转换，可以认为CGCS2000定位成果同属于WGS-84坐标系成果。

2.融合定位模型

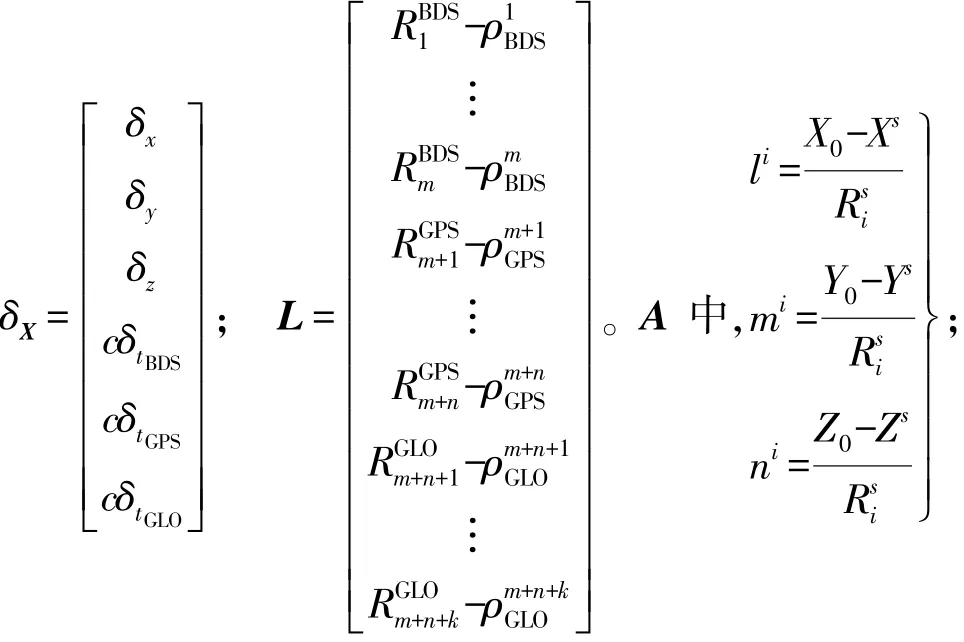
时空统一完成后，设接收机位置坐标为(Xr，Yr，Zr)，某星座一卫星位置为(Xs，Ys，Zs)，则融合系统的伪距观测方程可由式(1)统一表示为式中，，为接收机到该卫星的几何距离；ρsr对应伪距观测值；δtr为该星座系统下接收机钟差；c为光速。可以看出，融合系统的伪距观测方程形式与单系统的基本一致，不同之处在于时空统一后的三星座系统对接收机延迟误差并不相同。式(4)中含有6个待求参数，因此需要至少同时观测6颗卫星以完成融合定位解算。式(4)的线性化采用在接收机概略坐标(X0，Y0，Z0)处用泰勒级数展开，详见参考文献[9—10]，这里不再赘述。当观测卫星大于6颗时，根据冗余观测方程，利用最小二乘法进行求解。假设某一历元分别同时观测到m、n、k颗BDS、GPS、GLONASS卫星，则融合系统的误差方程可表示为(m＋n＋k)，s为不同星座卫星)，根据最小二乘求出δX值，进而得到该历元下接收机的位置坐标。为达到较高精度，将解算值回代作为接收机位置初值，对两次解算差值设一门限值，通过迭代计算，实现BDS/GPS/GLONASS高精度融合定位。

三、试验数据处理及分析

基于以上分析，为研究BDS/GPS/GLONASS融合系统的定位性能，于2013-01-08在中国测绘科学研究院位于河北某三系统试验站现场采集数据，接收机采样率为1 s，从15∶00∶00—23∶09∶59共9 h的数据，卫星截止高度角设为10°。基于时空统一的BDS/GPS/GLONASS融合定位模型，笔者以Visual Studio 2010为平台，利用C＋＋语言开发了BDS/GPS/GLONASS定位软件V1.0，分别以①BDS单系统、②GPS单系统、③GLONASS单系统、④融合三系统4种方案进行定位解算，并将定位结果与基准站已知精确坐标求差，将所得各分量残差转化到东北天坐标系(ENU)下，定位残差曲线如图3所示。

通过图3可以直观地看出，融合三系统各分量定位精度较BDS、GLONASS都有大幅提高；而与GPS的残差曲线近似，这是由于BDS、GPS、GLONASS三系统的定位精度各不相同。为了达到较高的精度，在系统融合时对不同的系统配置不同的权值，这里引用参考文献[3]结论，结合各系统的实际定位精度，对GPS、BDS、GLONASS系统按8∶2∶1进行配权，因GPS定位精度较高，配置的权比也相对较大，故而两残差曲线走势较一致。为详细研究定位结果，在图3的基础上，对各分量残差进行统计，结果见表2。

图3 BDS、GPS、GLONASS各单系统及其时空统一融合系统定位残差曲线

表2 BDS、GPS、GLONASS各单系统及其时空统一融合系统定位结果统计

由表2可以看出，通过时空统一，融合系统在N、E、U各分量较各单系统都有不同程度的提高，点位中误差达到2.53 m，较BDS、GPS、GLONASS分别提高68.68%、5.53%、76.54%。可以发现，融合系统较GPS仅提高5.53%，一方面是由于对GPS系统配置的权比较大；另一方面由于本试验测站GPS可见卫星最多达到11颗，最少也有7颗，平均维持在9颗左右，如图4、表3所示，充分多的冗余观测量，GPS单系统定位已达到很高精度(2.678 m)。而GLONASS大部分的可见星不多于7颗，最少时仅为5颗，冗余观测信息不足，必然会影响系统的定位精度。从图、表中还可以看出，BDS可见星维持在8～9颗，虽有充分多的冗余观测量，但是BDS空间卫星为GEO、MEO、IGSO 3种异质卫星构成的混合星座[7]。因5颗GEO卫星相对地球静止且全部可见，虽有相对较高的高度角，但加上其余的卫星整体构成的BDS空间几何结构较差，可以通过表征卫星空间分布优劣的GDOP可以看出这一点，如图4、表3所示。GDOP值越大，表明卫星分布范围越小，空间结构越差，定位精度也相对较低，这也正是BDS、GLONASS定位精度相对较低的直接原因。融合系统较各单系统都有不同程度的提高，从另一方面也论证了即便像GPS有较高的定位精度，通过系统的合理配权融合，依然可以提高定位精度，增加系统的稳定和连续性。

图4 BDS、GPS、GLONASS各单系统及其时空统一融合系统可见卫星数及GDOP值

表3基于图4，详细统计了各系统的可见星数、GDOP值。可以看出，融合系统的可见星数大幅提高，平均达到24.3颗，最大增幅达247.52%，是单系统的3倍还多。卫星数的增加有效改善了空间的卫星布局，GDOP值急剧下降，各系统DOP值降幅在50%左右，进而提高了导航系统的定位精度。可以预见，即便是在复杂环境(森林、峡谷)下，融合GNSS系统也不会因卫星数不足导致无法解算或信号中断，可有效改善系统的可靠性和连续性。

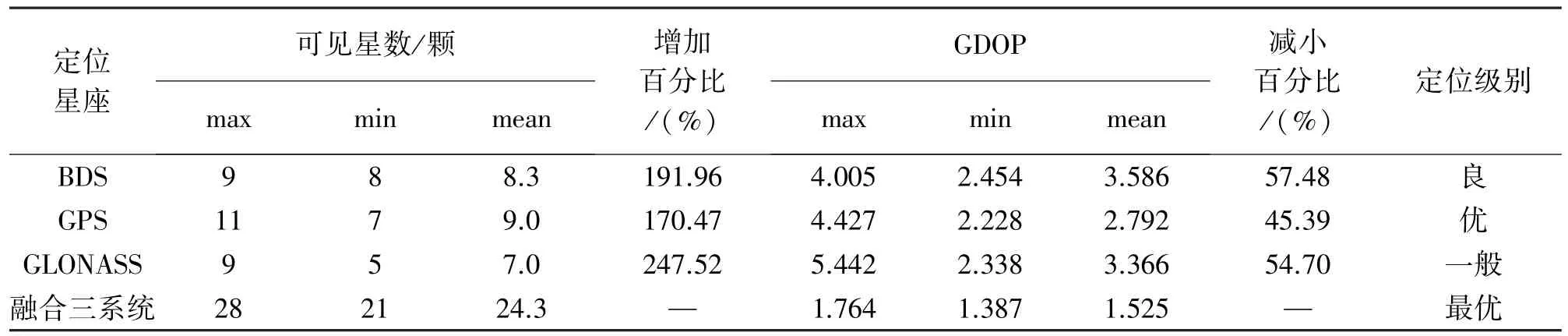
表3 BDS、GPS、GLONASS各单系统及其时空统一融合系统可见星数/GDOP/PDOP统计

四、结束语

传统GNSS单星座系统定位一方面因环境限制(森林、建筑物遮挡)使可见星数目降低，导致定位精度降低甚至发生服务中断；另一方面稳定性不强、自主安全性差，一旦拒绝提供服务而使用户无能为力。特别是BDS当前还仅是覆盖亚太的区域导航系统，为充分利用GNSS资源，最大限度地发挥BDS的优势，为用户提供高精度、高可靠性、高动态的PNT服务，加强GNSS系统间的兼容与互操作，研究GNSS融合定位是当前基于BDS研究的核心和关键技术。

本文以更高精度和可靠性为原则，基于单点定位，在时空统一上建立BDS/GPS/GLONASS融合定位模型，通过三系统实测数据进行融合定位解算。结果表明，BDS/GPS/GLONASS融合卫星导航系统能够提供3倍于单系统的可见卫星数量和导航定位信号，有效改善空间卫星布局，降低精度衰减因子(DOP)，大幅提升各导航性能指标，对我国BDS的建设和GNSS多模融合定位的研究具有一定的参考意义。

[1] 高星伟，葛茂荣.GPS/GLONASS单点定位的数据处理[J].测绘通报，1999(4)：8-9.

[2] DAI L，RIZOS C，HAN S.An Adaptive Procedure for Carrier Phase-based GPS/GLONASS Positioning[J]. Geomatics Res Australasia，2003(78)：19-36.

[3] 蔡昌盛，戴吾蛟，匡翠林.GPS/GLONASS组合系统的PDOP计算和分析[J].测绘通报，2011(11)：5-7.

[4] HEWITSON S，LEE H K，WANG JINLING.Localizability Analysis for GPS/Galileo Receiver Autonomous Integrity Monitoring[J].Journal of Navigation，2004，57(2)：245-259.

[5] 王潜心，陈正阳，唐利民.基于相对定位模型的GPSGalileo组合定位研究[J].测绘科学，2009，34(1)：63-65.

[6] 高星伟，过静珺，程鹏飞，等.基于时空系统统一的北斗与GPS融合定位[J].测绘学报，2012，41(5)：743-748.

[7] 中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B1Ⅰ(1.0版) [R].北京：[s.n.]，2012.

[8] 党亚民，秘金钟，成英燕.全球导航卫星系统原理与应用[M].北京：测绘出版社，2007.

[9] 徐绍全，张华海，杨志强，等.GPS测量原理及应用[M].武汉：武汉大学出版社，2003.

[10] 魏子卿.2000中国大地坐标系及其与WGS84的比较[J].大地测量与地球动力学，2008，28(5)：1-5.

[11] 陈义.利用精密星历进行单点定位的数学模型和初步分析[J].测绘学报，2002，31(S1)：31-33.

Research on Model and Performance of BDS/GPS/GLONASS Multi-mode Fusion Positioning

LI Hefeng，DANG Yamin，BEI Jinzhong，GU Shouzhou，ZHANG Decheng

P228.4

B

0494-0911(2014)09-0001-05

2013-06-27

国家863重点项目(2011AA120503)；科技部科技支撑计划(2012BAB16B01)；国家863计划(2013AA122501)；北斗分析中心建设与运行维护(GFZX0301040308-06)

李鹤峰(1987—)，男，河南平舆人，硕士生，主要研究方向为GNSS多模融合定位与RAIM算法。引文格式:李鹤峰，党亚民，秘金钟，等.BDS/GPS/GLONASS融合定位模型及性能分析[J].测绘通报，2014(9)：1-5.

10.13474/j.cnki.11-2246.2014.0280