一种基于拼接线和动态基准的影像拼接方法

徐景中，袁 芳，寇 媛

(武汉大学遥感信息工程学院，湖北武汉 430079)

一种基于拼接线和动态基准的影像拼接方法

徐景中，袁 芳，寇 媛

(武汉大学遥感信息工程学院，湖北武汉 430079)

针对无人机影像拼接处理中易产生鬼影、错位等问题，提出一种基于拼接线和动态基准的影像拼接方法。该方法首先采用改进Duplaquet方法搜索最优拼接线，拓宽了拼接线的扩展方向；然后采用动态基准影像拼接策略，降低累积误差的影响；接着提出最终基准影像的选择方法，并在最终基准影像坐标系下实现多幅无人机序列影像拼接。试验结果表明，该算法能够有效解决传统拼接方法中所遇到的拼接线问题，同时能够避免变换误差较大的影像对后续拼接影像的影响，获得更好的拼接结果。

无人机序列影像；拼接线；动态基准；最终基准影像；影像拼接

一、引 言

无人机遥感因具有机动、快速的响应能力，能够获取高分辨率图像，受天气影响小等优势，已成为行业学者和工作者关注的焦点。但是受无人机飞行高度的限制，获取的单幅影像覆盖范围有限，要得到完整覆盖目标区域的影像就需要对不同时刻获取的序列影像进行拼接。因此，对如何实现影像的有效拼接，减少拼接误差的研究是十分必要的。

目前已有部分学者对此进行了相关研究。针对拼接中出现鬼影、错位等问题，张媛等将影像颜色差平方作为准则值，加入重力系数来检测最优拼接线，该算法没有考虑影像结构差，在实际中不易找到最优拼接线[1]；王军等根据重叠区域像素点间的相关性计算各像素点的准则值，但是采用复杂度很高的Dijkstra算法查找最佳拼接线，该算法速度比较慢[2]；党建武等提出搜索拼接线时优先考虑影像特征点，以此减少拼接线上可能出现的误差点，但重叠区域的特征点数量有限，对减少误差的作用不是很大，而且增加了计算时间[3]；谢鹏提出的随机贪心算法搜索最优拼接线，从重叠区域中心线附近搜索最优拼接线，该算法得到的是一个局部最优解[4]；针对拼接中累积误差，多次变换引起的影像失真等问题，李从利等在连续拼接过程中采用变换基准图的拼接策略来消除累积误差，以中间帧为最终基准图减少图像失真，有效地减小了连续拼接中误差的累积，但是要以中间影像本身变形较小为前提，否则也会产生较大的误差[5]；何敬等选取航带中间4幅影像作为备选影像，再从中选择地物最为丰富、与邻近影像匹配特征点最多的影像作为最佳影像，该算法比较适用于影像数目较少的拼接[6]。

本文在已有方法的基础之上，针对影像拼接中累积误差，鬼影、错位等问题，提出一种基于拼接线和动态基准的影像拼接方法。

二、算法原理与方法

为了实现基于拼接线和动态基准的无人机影像拼接，本文重点开展了拼接线搜索、动态基准拼接策略、最终基准影像选择算法研究。该方法总体流程如图1所示。

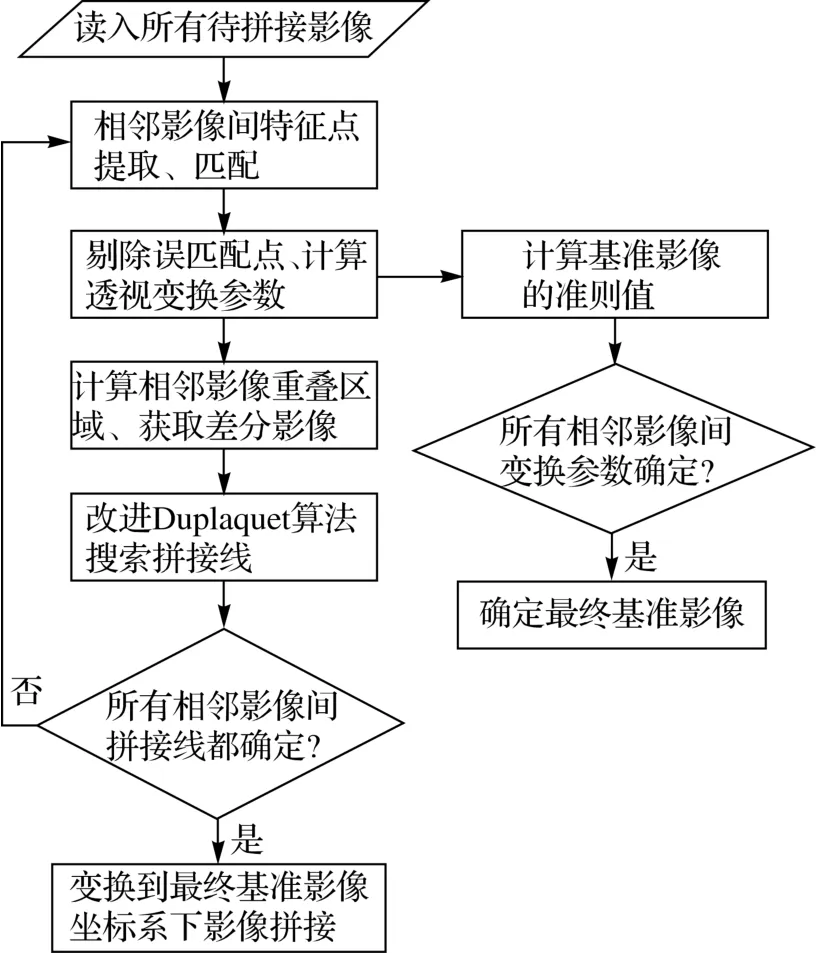
图1 算法流程图

上述流程中，首先采用具有良好的尺度、旋转、光照等不变性的SIFT算法[7-8]进行特征点提取、匹配，利用RANSAC算法[9]剔除误匹配点，并利用提纯后匹配点计算透视变换参数；然后在Duplaquet[10]算法基础上定义一组新的模板计算拼接线准则值，并拓宽拼接线的扩展方向；接着以第2幅到第n-1幅影像(设有n幅影像)中的每一幅影像为基准影像，利用其与相邻影像间的透视变换参数和同名点计算其准则值，取准则值最小的基准影像为最终的基准影像；最后进行影像拼接。

1.检测拼接线

(1)计算拼接线准则值

Duplaquet在1998年提出了一个最优拼接缝搜索准则[10]

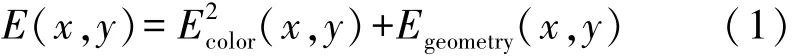
式中，Ecolor(x，y)表示两幅影像重叠区域像素点的灰度值之差；Egeometry(x，y)表示两幅影像重叠区域像素点的梯度值之差。

影像梯度值可以采用sobel算子[11]计算，但经典的sobel算子在计算过程中利用水平和垂直两个方向的模板，即

这两个模板既没有考虑对角线方向上的信息，也没有考虑到像素点周围结构的相似性，因此，不能够找到最优拼接线。在考虑到像素点8方向上的信息，以及像素点周围结构相似性的基础上，本文定义一组新的模板。

式中，I(x，y)表示坐标点为(x，y)的像素点的灰度值；Sn表示8方向的Sobel算子模板。

(2)确定最优拼接线

若有重叠区域为n×m的两幅影像，则能找到n条备选拼接线，每条拼接线搜索的具体步骤如下：

1)将第一行每一列像素点作为每条拼接线的起点，各点的强度值为按式(1)计算得到的准则值，每条拼接线的第二个备选点取对应列的第二个像素点。

2)从第二行起，对位于重叠区域最左边和最右边的像素点检测当前行和下一行3个方向的像素点，其他位置上的点检测当前点所在位置的左、右及下一行3方向，共5个相邻像素点，将计算得到的5邻域中准则值最小的点作为备选拼接线上的下一个点，重复该步骤，直到重叠区域的最后一行。

3)重复上述步骤，直到n条备选拼接线都确定，从所得到的所有拼接线中选择平均强度值最小的一条作为最佳拼接线。

最佳拼接线搜索算法如图2所示。

图2 最优拼接线搜索途径

图2中，m、n表示重叠区域的高度、宽度；Ei表示第i个像素点的准则值，黑色圆点表示拼接线上的备选点。

2.动态基准

设有n幅影像f1、f2、…、fn连续拼接，第i次(1＜i＜n)配准以fi为待配准图，以fi＋1为基准影像，透视变换矩阵为Hi，i＋1。将第i-1次的匹配准图fi-1，i(即所有变换到fi坐标系下的影像)根据变换矩阵Hi，i＋1变换到fi＋1影像坐标系下。这样每次图像变换都是按照本次图像配准的变换矩阵把上次配准的结果图变换到新的基准影像坐标系下，就避免了连续重采样，也就减小了重采样导致的累积误差。因此，在拼接过程中，基准影像随拼接影像的位置在不停的变换。

3.搜索最终基准影像

影像拼接需要将所有影像变换到同一坐标系下才能拼接成一幅全景图像，拼接坐标系的变换方式选取决定了拼接后影像的精度和形状[13]。综合考虑变换过程中的复杂度、固定基准影像引起后续拼接影像的变形程度，本文利用透视变换参数和同名点确定最终基准影像。

(1)判定基准影像的准则

以水平方向上的两幅相邻影像为例，两幅相邻影像上同名点间的关系式可以表示为

(2)确定基准影像

若有n幅待拼接影像，计算从第2幅到第n-1幅影像间的任一影像k的准则值，将准则值最小的影像视为基准影像，即

式中，Tk-1是第k-1幅影像与第k幅影像间同名点对数；(xi，yi)是第k-1影像上同名点；a1、b1分别为第k-1幅影像投影到第k幅影像坐标系下的第7、8个透视变换参数；Tk＋1是第k幅影像与第k＋1幅影像间同名点对数；(x′j，y′j)是第k＋1幅影像上同名点；a2、b2分别为第k＋1幅影像投影到第k幅影像坐标系下的第7、8个透视变换参数。

三、试验结果与分析

为了验证文中算法的有效性，本文利用Visual C＋＋编程实现了本文的拼接算法，分别采用天津和安阳某实地无人机影像进行试验分析。

为了验证本文拼接线算法的有效性，以天津某地区的一组影像为试验数据进行试验，该地区楼房等高大建筑物比较多，影像分辨率比较高，图3(a)、(b)所示为该地区两幅待拼接影像。并将本文算法拼接结果图与Duplaquet算法拼接结果图进行对比分析。图4所示为本文方法搜索最优拼接线进行影像拼接的结果图，图5所示为Duplaquet算法搜索拼接线进行影像拼接的结果图，图中黑框中曲线是拼接影像的拼接线。从图4中可以看出，本文中采用的改进拼接线检测方法能够使房屋绕开重叠区的高大建筑物，使得两张影像没有明显的拼接痕迹。

图3

图4 本文拼接算法结果

图5 Duplaquet方法拼接结果

Duplaquet算法在搜索拼接线时，从当前像素点的下一行临近的3个像素点中寻找下一个备选点，因此，拼接线的长度与重叠区域的高度相同。本文中算法，在找拼接线备选点时，为避免拼接线穿过房屋等高出地表物体的水平边缘，考虑当前像素点水平方向上的点，因此，搜索到的每一条拼接线的长度都是不等长的。表1列出了两种算法拼接线的长度与重叠区域的高度，通过比较表1中数据，可以看到本文中算法拼接线长度比Duplaquet算法中拼接线长度长。

表1 拼接线长度对比列表像素

以安阳某地区7张影像为试验数据，采用第二章第1节中算法搜索最优拼接线，采用本文中第二章第3节算法确定最终基准影像，表2列出了按本文方法计算求得的第2幅到第6幅影像作为基准影像的准则值。从表2中可以看出第二幅影像的准则值最小，因此以第二幅影像为基准影像。图6所示为以第二幅影像为基准影像的单航带序列影像拼接结果，从拼接结果图可以看到，拼接线能够很好地绕过建筑物，其中黑框中曲线为拼接线。

表2 影像准则值

图6 单航带序列影像拼接结果

为从整体上降低图像失真的程度，减小变形误差，在拼接时从两端开始，以第二章第3节中算法选择的基准影像作为最终基准图，利用第二章第2节中动态基准策略拼接。

若有n幅影像，当n＞3时，若第t( 1＜t＜n)幅影像为本文中方法找到的基准影像，对前t-1幅影像变换到基准影像坐标系下，总共需要经过次变换；对后n-t幅影像变换到基准影像坐标系下，共需经过次变换。若采用第一幅影像为基准影像，后n-1幅影像变换到基准影像坐标系下，共需经过次变换。这样，本文中提出搜索最优基准影像的算法既没有增加算法复杂性和程序运行的时间，又降低了图像由于透视变换影像的失真程度。结合图6的拼接结果可以看出，利用最优拼接线和动态基准影像进行拼接，可以得到理想的拼接结果。

四、结束语

本文在分析现有的无人机序列影像拼接算法的基础上，针对地物复杂的特点，采用检测最优拼接线方法，很好地解决了错位和鬼影等问题。针对拼接中的累积误差和连续变换导致的影像失真等问题，以透视投影变换为基础，通过动态基准和选择最终基准影像使之得到解决。但同时也存在不足的地方，当待拼接影像间的光照强度不同时，拼接影像在拼接线两侧呈跳跃式的变化。以后需要对重叠区域进行影像融合，对影像拼接线附近进行亮度调整，以达到更好的拼接效果。

[1] 张媛，高冠东，贾克斌.运用特征点匹配的柱面全景图像快速拼接算法[J].中国图象图形学报，2009，3(3)：247-250.

[2] 王军，朱宝山，朱述龙，等.基于相关系数的遥感图像拼接线检测算法[J].测绘与空间地理信息，2011，34(3)：151-153.

[3] 党建武，宗岩，王阳萍.基于SIFT特征检测的图像拼接优化算法研究[J].计算机应用研究，2012，29(1)：329-332.

[4] 谢鹏.基于贪心搜索的正射影像拼接方法[J].中国科技信息，2013(2)：74-77.

[5] 李从利，薛模根，冷晓艳，等.空中侦察序列图像连续拼接的累积误差分析与消除[J].中国图象图形学报，2008，13(14)：814-819.

[6] 何敬，李永树.基于特征点和最优路径的无人机影像拼接方法[J].遥感技术与应用，2012，27(2)：173-176.

[7] LOWE D G.Object Recognition from Local Scale-Invariant Featrues[C]∥International Conference on Computer Vision.[S.l.]：IEEE，1999：1150-1157.

[8] LOWE D G.Distinctive Image Features from Scale-Invariant Keypoints[J].International Journal of Computer Vision，2004，60(2)：91-110.

[9] FISHCHLER M A.Random Sample Consensus：A Paradigm for Model Fitting with Appliction to Image Analysis and Automated Cartography[J].Communication Association Machine，1981，24(6)：381-395.

[10] DUPLAQUET M L.Building Large Mosaics with Invisible Seam-Lines[C]∥Proc.SPIE Aerosense.Orlando：[s.n.]，1998.

[11] GONZALEZ R C，WOODS R E.Digital Image Processing[M].2nd ed.Beijing：Publishing House of Electronics Industry，2007：105-107.

[12] 徐亚明，邢诚，陈晓东.一种基于拼接线的无人机序列影像拼接方法[J].武汉大学学报：信息科学版，2011，36(11)：1265-1269.

[13] 李明，刘欢，朱欣焰.一种面向灾害应急的UAV影像快速拼接方法[J].灾害学，2012，27(3)：139-144.

更正

本刊2014年第8期第134页《Trimble V10影像流动站在城市测量中的应用》一文中，作者郭玉强、尹国斌的单位应分别为“山西省煤炭地质115勘查院测绘技术中心，山西大同037003；北京麦格天渱科技发展有限公司，北京100043”。特此更正，并向作者、读者致歉。

本刊编辑部

An Image Mosaic Method Based on the Seamline and Dynamic Datum

XU Jingzhong，YUAN Fang，KOU Yuan

P23

B

0494-0911(2014)09-0034-04

2013-07-19

国家科技支撑项目(2012BAH34B02；2011BAH12B04)

徐景中(1980—)，男，江苏淮安人，博士，副教授，主要研究方向为LiDAR数据分析与处理。引文格式:徐景中，袁芳，寇媛.一种基于拼接线和动态基准的影像拼接方法[J].测绘通报，2014(9)：34-37.

10.13474/j.cnki.11-2246.2014. 0288