某国产发动机曲轴轴系扭转振动激励力矩的识别

廖中文，高俊文，王海林

(1.广东农工商职业技术学院机电系，广州 510507; 2.华南农业大学工程学院，广州 510642)

某国产发动机曲轴轴系扭转振动激励力矩的识别

廖中文1，高俊文1，王海林2

(1.广东农工商职业技术学院机电系，广州 510507; 2.华南农业大学工程学院，广州 510642)

在进行多级橡胶扭转减振器中各级扭转减振器的参数设计时，需要对简谐力矩进行精确计算。探讨了曲轴轴系激励力矩的识别问题，通过自编Matlab程序，以试验中所得到的气体压力为基础，结合某国产发动机的参数，对曲轴轴系的激励力矩进行了识别，得出激励力矩各个简谐分量的幅值和相位。结果表明:发动机转速与曲轴扭转激励力矩的基频之间的比值不随转速变化而变化，与理论推导一致。

扭转振动;行驶平顺性;简谐力矩;多级扭转减振器;激励力矩

良好的行驶平顺性和低噪声可以提升汽车的舒适性。能影响汽车行驶平顺性和产生噪音的因素之一是发动机振动。发动机振动的能量最终会传递到车身上，造成车身振动加剧、噪音加大，并且会影响到车辆行驶的动力性和经济性［1－2］。目前，降低发动机振动的主要方法之一是加装扭转减振器［3－4］。由于单级扭转减振器已经满足不了大功率、高转速发动机的减振需求，所以越来越多的发动机上加装了多级扭转减振器。不过由于其结构的复杂性，国内大多数厂家还停留在仿造阶段，对多级扭转减振器的参数不能进行有效的确认设计。本文以某国产发动机参数为例，旨在对发动机曲轴轴系扭转振动激励力矩进行识别，为多级扭转减振器的参数设计提供参考依据。

1 曲轴轴系扭转振动激励力矩的产生机理

根据力学分析可知，作用在曲柄－连杆机构上的力和力矩有气缸内气体作用力、运动质量惯性力、支撑反力、旋转阻力矩和摩擦力(矩)。摩擦力(矩)主要取决于运动零件的制造质量与润滑情况，其数值相对较小，在对机构进行受力分析时可以忽略不计。根据达朗贝尔原理及动静法可知，其他各力(矩)达到平衡，受力分析如图1所示。对活塞进行受力分析，可得到平衡方程(1)。

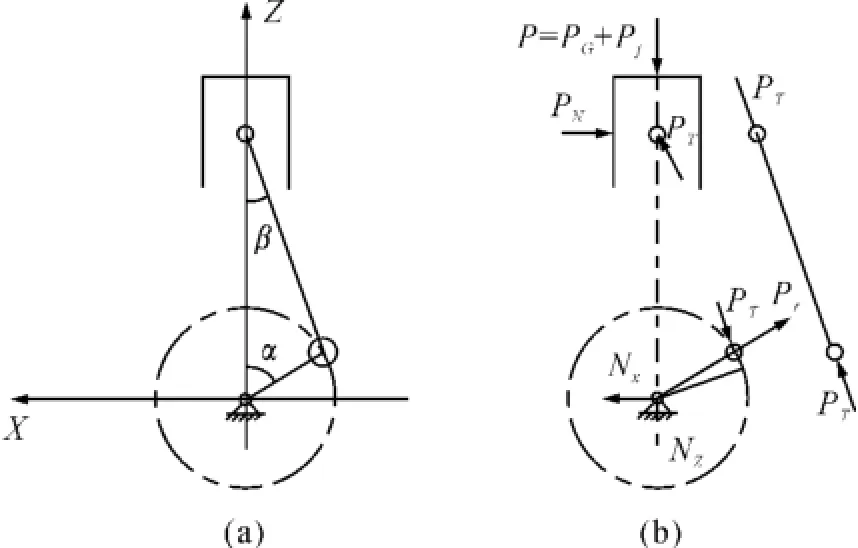
图1 曲柄连杆机构总体受力分析示意图

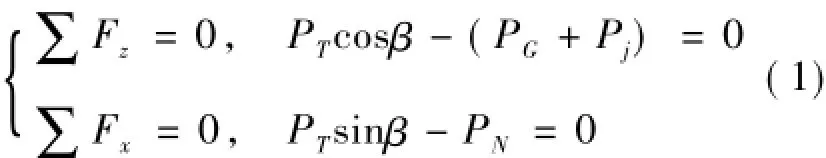
图1和式(1)中:PG为气体对活塞的作用力; Pj为往复惯性力;Pr为旋转惯性力;PN，P'N为垂直于活塞中心线的侧推力;PT为活塞连杆间的内力。

连杆的轴向力PT和活塞的侧向压力PN可以表示为

由此可得，迫使曲轴旋转的主动力矩方程为

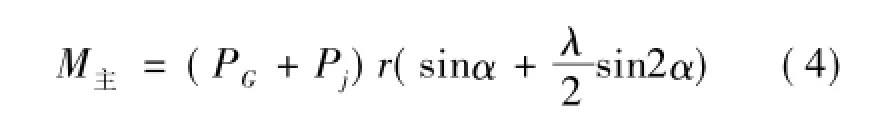
由于主动力矩M主中PG，Pj都随曲柄转角α变化，因而M主是随α变化的周期性函数。在周期性变化的干扰力矩作用下，发动机曲轴的运动包括两部分:一部分是在平均扭矩M0作用下的以角速度ω所进行的匀速旋转运动;另一部分是在各次简谐力矩的作用下所产生的不同频率的简谐振动。这种对主动力矩的分析工作被称作简谐分析。在扭振的强迫振动分析中，一般先研究各次简谐力矩对轴系激起的振动，然后根据线性叠加原理将它们依次叠加，从而确定整个主动力矩对轴系造成的扭转振动。

根据牛顿二项式定理，简化方程(3)可得

2 曲轴轴系扭转振动激励力矩的识别

激励力矩主要由两部分构成:气体爆发压力所引起的干扰力矩及曲柄连杆机构惯性力所引起的干扰力矩［5－6］。

本文以某国产发动机为研究对象，发动机的主要参数如表1所示。

表1 发动机主要参数

通过实测，得到1 000～5 000 r/min转速范围内气缸内爆发压力相对于曲轴转角的变化。编制Matlab程序进行模拟计算，得到发动机曲轴转矩相对于曲轴转角的变化规律，并识别出发动机曲轴主动力矩的各次简谐力矩，为分析曲轴强迫振动提供参考。

通过实测统计发现，各个转速下的气缸爆发压力在曲轴转角为20°±10°时达到最大值。由于此时发动机火花塞点火，缸内混合气被点燃，热量迅速膨胀，推动活塞连杆机构运动。气缸爆发压力随转速的升高而增加，在一定转速时达到峰值，再升高转速压力会降低。在发动机转速为1 000 r/min时，气缸爆发压力最低，约为3.8 MPa，而当发动机转速为4 500 r/mim时，气缸爆发压力最高，约为6.05 MPa。在中高转速时气缸爆发压力变化幅度相对较小，每500 r/min间隔压力变化约为0.2 MPa;而在低速时气缸爆发压力变化幅度相对较大，1 000 r/min与1 500 r/min的压力相差达到了约0.6 MPa。

现以最大、最小气缸爆发压力及最高转速对应的气缸爆发压力为研究对象，即发动机转速分别为1 000，4 500及5 000 r/min时，对曲轴轴系的激励力、激励力矩进行研究，并作简谐分析，结果如图2所示。

将实验测得的气缸爆发压力数据及发动机曲轴轴系的具体参数导入Matlab程序进行计算，从而得到发动机曲轴轴系的激励力、激励力矩及其各次简谐力矩(图3～5)。

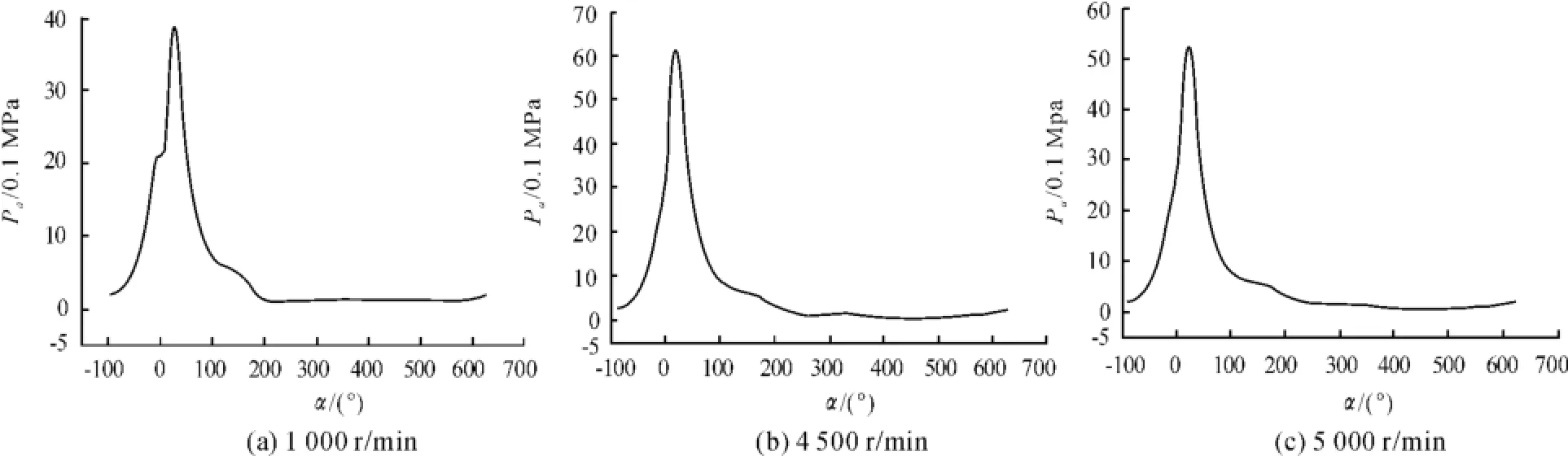
图23 种转速对应的气缸爆发压力曲线

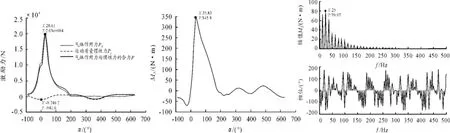
图31 000 r/min对应的激励力矩识别分析图

图44 500 r/min对应的激励力矩识别分析图

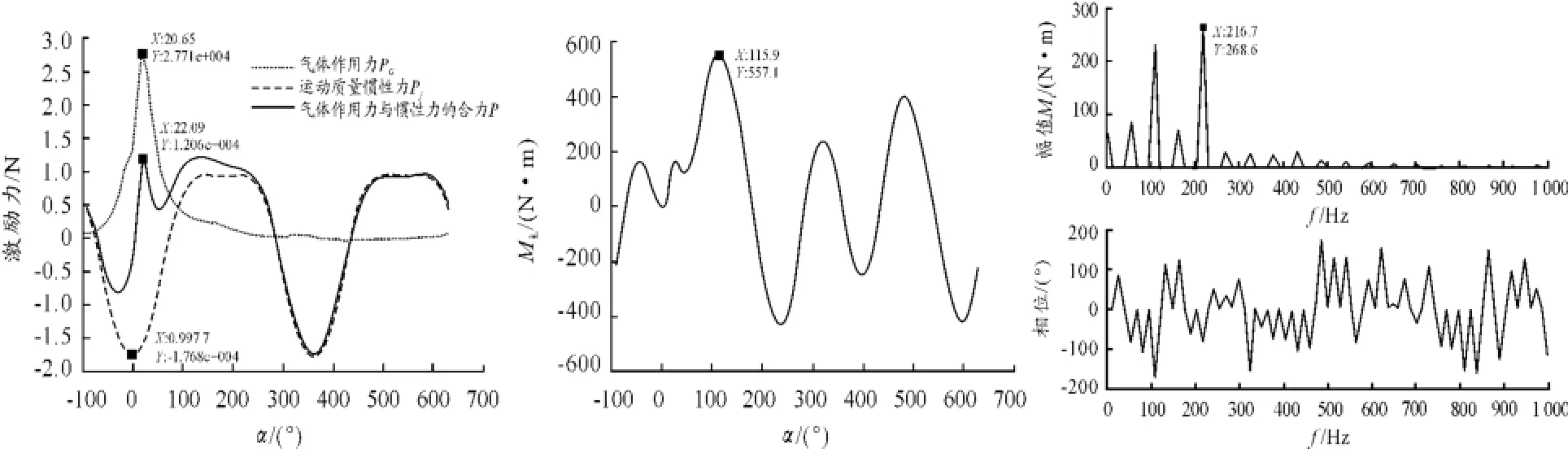
图55 000 r/min对应的激励力矩识别分析图

1)比较图3～5的第1个图(参照图2)，可以发现:气体作用力PG先是随着发动机转速的升高而增大，当达到一个峰值之后，PG又会随着转速的升高而有所下降。运动质量惯性力Pj的绝对值随着发动机转速的升高而增大。在低转速(怠速工况)情况下，气体作用力PG与运动质量惯性力Pj的合力曲线几乎与PG的曲线重合，运动质量惯性力Pj对激励力的贡献很小;而随着转速的提高，Pj急剧增加，大大缓解了做功行程中气体爆发压力对曲轴的扭转振动激励力的影响，使激励力的合力变得稍微平缓。在排气行程、进气行程及部分压缩行程中，激励力的合力主要来自于运动质量惯性力。

2)比较图3～5的第2个图，即曲轴扭转的主动力矩相对于曲轴转角的变化曲线。随着转速的提高，曲轴扭转的主动力矩的波动变大，其最大值也逐渐增大。在较高转速或高转速下，与主动力矩的最大值对应的曲轴转角要比气体作用力的最大值所对应的曲轴转角落后约90°。

3)比较图3～5的第3个图。对应发动机转速为1 000 r/min的曲轴扭转激励力矩经过Matlab计算后得到的基频为8.2 Hz，前3个谐次所对应的幅值相差不大，其中2倍频所对应的幅值最大，约80 N·m.。对应转速为4 500 r/min的基频约为37.5 Hz，2倍频和4倍频所对应的幅值较大，其中2倍频所对应的幅值最大，为201.1 N·m。对应转速为5 000 r/min的基频约为41.5 Hz，2倍频和4倍频所对应的幅值较大，其中4倍频所对应的幅值最大，为268.6 N·m。发动机转速与曲轴扭转激励力矩的基频之间关系如表2所示。

表2 发动机转速与曲轴扭转激励力矩的基频之间的关系

观察表2不难发现，发动机转速与曲轴扭转激励力矩的基频之间比值约为120，这与理论推导也一致。因为该发动机为4缸，曲轴每转2圈一个工作循环结束，干扰力矩周期变化一次，显然干扰力矩的圆频率是曲轴角速度的一半，其谐次应该为0.5，1，1.5，2，……。这里所说的基频实际上是对应0.5谐次时的频率。

3 结束语

本论文以简谐分析为主线，着力于解决扭转振动激励力矩的识别问题，为多级扭转减振器的参数设计工作打下基础。简要分析了发动机曲轴轴系扭转振动激励力矩产生机理，并且对3种特殊转速下的激励力矩进行了识别分析。分析结论与理论推导一致，从而验证了分析过程的正确性，对后续的研究设计工作起到指导作用。

［1］吕兴才，舒歌群，沈红斌.汽车发动机曲轴纵向振动的研究［J］.汽车工程，2001，23(5):332－336.

［2］杨礌.汽车发动机曲轴扭转振动分析及控制［D］.重庆:重庆大学，2005:45－55.

［3］吕振华，冯振东.汽车发动机曲轴阻尼式扭振吸振器设计方法探讨及应用［J］.内燃机工程，1992，13(3): 27－33.

［4］陈超.汽车发动机曲轴系统扭转振动分析与减振器匹配的研究［D］.广州:华南理工大学，2012:8－15.

［5］李晓峰，袁兆成，赵福全，等.4D20轿车柴油机曲轴系统动力学分析［J］.汽车技术，2010(12):21－25.

［6］吴红亮.DF7柴油机曲轴设计开发［M］.北京:清华大学，2011:23－30.

(责任编辑 刘舸)

High-speed Visualization Shear Viscosity Tester Development
and Accuracy Checking

LIAO Zhong－wen1，GAO Jun－wen1，WANG Hai－lin2
(1.Mechanical and Electrical Department，Guangdong AIB Polytechnic College，Guangzhou 510507，China;2.School of Engineering，South China Agriculture University，Guangzhou 510642，China)

When all levels of torsional vibration damper’s parameters is designed of multistage rubber torsional damper，and precise calculation of harmonic torque is needed.This paper mainly discusses the problem of crankshaft axis excitation torque identification.The Matlab program is compiled.Based on the experiment of gas pressure，and combined with parameters of a domestic engine and identification of the crankshaft axis excitation torque，it can identify different harmonic excitation torque component of the amplitude and phase.The results show that the ratio between the engine speed and fundamental frequency of crankshaft torsional excitation torque does not changes over speed，consistent with the theoretical derivation.

torsional vibration;riding comfort;harmonic torque;multistage reverse shock absorber; excitation torque

U461.4

A

1674－8425(2014)03－0039－05

10.3969/j.issn.1674－8425(z).2014.03.008

2013－10－25

广东省科技计划项目(2008B021200008)

廖中文(1984—)，男，湖北武穴人，硕士，主要从事车辆系统动力学研究;通讯作者王海林(1972—)，男，河北宣化人，博士，教授，主要从事机械动力学与摩擦学研究。

廖中文，高俊文，王海林.某国产发动机曲轴轴系扭转振动激励力矩的识别［J］.重庆理工大学学报:自然科学版，2014(3):39－43.

format:LIAO Zhong－wen，GAO Jun－wen，WANG Hai－lin.High－speed Visualization Shear Viscosity Tester Development and Accuracy Checking［J］.Journal of Chongqing University of Technology:Natural Science，2014 (3):39－43.