径流量预测的PWM方差分析法

张云，袁永生，戴启璠

(1.河海大学理学院，南京 211100;2.江苏省灌溉总渠管理处，江苏淮安 223200)

径流量预测的PWM方差分析法

张云1，袁永生1，戴启璠2

(1.河海大学理学院，南京 211100;2.江苏省灌溉总渠管理处，江苏淮安 223200)

径流量预测一直是一个重要的研究课题，目前已有很多预测模型，但都有其适用条件。基于方差分析的周期延拓法在预测径流量时，小样本数据均值易受异常点影响。针对该问题，改进PWM值代替传统均值对时间序列进行径流量预测，并与传统ARMA模型进行了比较。结果显示:PWM方差分析法可行，并且误差较小。

径流量预测;方差分析;周期延拓;改进PWM方法

我国是一个多河流的国家，水文系统的状况与河流的水情对当地的民生与发展至关重要。快速准确地进行径流量预报可以及时预测旱情与涝情，减少灾害的影响与范围，从而更好地利用水流量进行调节。因此，良好的径流量预测十分重要。

目前，水文系统的径流量预测已有大量的模型，如自回归移动平均模型(ARMA模型)［1］、马尔科夫链模型［2］、多元线性回归模型［3］、优选因子集成模型［3］、周期均值叠加模型［4－5］等。由于水文系统是受各种环境与气象因素影响的复杂的动力系统，因而对水文时间序列建筑模型的分析十分困难。上述的模型有不同的适用条件，一般不存在能适用于所有时间序列的最优模型。

本文将周期均值叠加预测模型与改进PWM (projection depth weighted mean)方法［6－7］相结合，利用水文序列的周期性提取若干优势周期，并用各小样本数据的改进PWM值取代传统均值，采用加权处理的Bootstrap抽样方法，通过数据模拟比较了PWM方法与ARMA模型。结果表明，结合了改进PWM方法的周期叠加法更加稳健。本文以滦河潘家口水库数据资料为例证明了该方法的可行性。

1 改进PWM方法

PWM方法通过合理引进权函数，使得异常点对均值的影响减弱。同时，利用修正的Bootstrap抽样方法对小样本数据进行抽样，再用百分位法对各PWM值进行截取，从而得到更稳健的预测区间。设原样本为Xi，i=1，2，…，n，其步骤如下:

说明:Bootstrap样本获取方法有许多种，上述修正的Bootstrap抽样法在样本量较少的情况下对总体的反应较好，并且曲线平滑，对原始样本进行了优化。

2 方差分析法

3 实例分析

本文数据为海河水利委员会的原始实测数据，使用滦河潘家口水库站1929—2001年总月径流量资料来预测未来几年的总径流量。具体步骤如下:

1)时间序列平稳化

通过EViews对数据的分析，可以明显看出时间序列是非平稳的。因此对原始数据取对数减弱其震荡，并进行一阶差分去除了原始时间序列中的趋势。

2)方差分析确定优势子周期［10］

利用Excel自带的方差分析法，逐步提取了F值最大的优势子周期，在给定置信水平为0.05的情况下，推出平稳后的数据含有周期为4、5、17、21的子周期。

3)用改进PWM方法计算周期震荡波

在一般的方差分析中，用均值来计算周期的震荡波作为周期延拓的基础，但是当组内样本量很少的时候，均值很容易受到异常点的影响，因此得出的结果不太精确。本研究利用改进的PWM值来代替均值做周期延拓。

PWM方法合理引进权函数以降低异常数据的影响，同时修正的Bootstrap方法在小样本情况下对总体反应较好，对原始数据进行了平滑处理。对于每一个子周期，分别计算出其振荡周期的PWM值，令不同周期的同一时刻取值叠加，就得到了预测模型。

4)还原原始模型

预测模型建立在原数据取对数再差分后的结果上，因此需要对步骤3)得到的预测模型进行还原。最后得到原始数据与模型数据的对比，如图1所示。

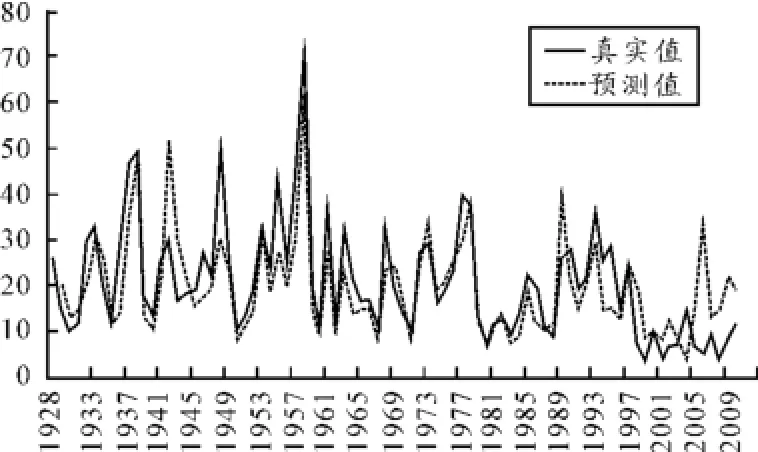
图1 模型拟合情况

模型在样本数据内拟合效果较好，但是在预测区效果不佳，经计算，预测区的采用PWM方差分析法得到的MAPE值为145.95。原因是样本离散程度大，存在过大和过小异常点，使得预测效果不佳。

5)模型对比

使用ARMA模型［1］建立了ARMA(4，1)模型，并建立了二阶差分的表达式:

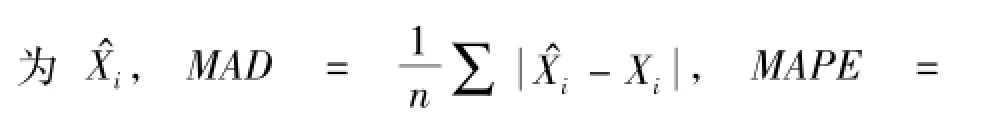
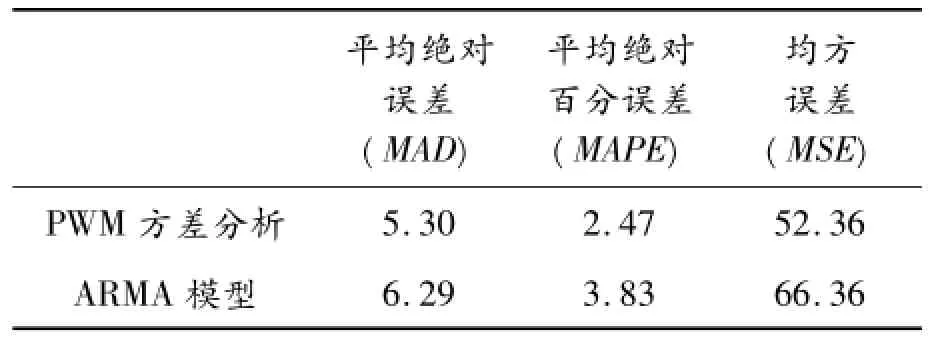
表1 预测精度对比

经计算，可得PWM方差分析法的拟合精度优于ARMA模型法。

4 结束语

在对滦河潘家口水库站径流量分析和预测中，对数据进行了取对数和一阶差分使其平稳，再用方差分析法分析出优势子周期，用基于修正的Bootstrap抽样方法计算的改进PWM值代替数据均值，使得预测结果更为稳健，削弱了异常点的影响。同时将该方法与传统ARMA模型进行比对，得出PWM方差分析法结果更优的结论。

［1］王勇，顾海燕，徐文科.基于ARMA模型的河川径流量预测［J］.哈尔滨商业大学学报:自然科学版，2011，27 (3):320－323.

［2］邱林，安可君，王文川.基于Bayes分类的Markov径流量预测模型［J］.水利科技与经济，2011(12):1－4.

［3］李杰友，熊学农.水库月径流中长期预报系统的开发研究［J］.水利水电科技进展，1998，18(3):32－38.

［4］黄燕，张静怡，顾鹤南.基于均生函数模型的香屯站年最高水位模拟与预测［J］.南水北调与水利科技，2010，8(1):72－74.

［5］左其亭，高峰.水文时间序列周期叠加预测模型及3种改进模型［J］.郑州大学学报:工学版，2004，25(4): 67－73.

［6］Yijun Zuo.Data Depth Trimming Counterpart of the Classical t(or T2)Procedure［J］.Journal of Probability and Statistics，2009.

［7］Yijun Zuo，Hengjian Cui，Xuming He.On the Stahel－Donoho Estimator and Depth－weighted Means of Multivariate Data［J］.The Annals of Statistics，2004，32(1):167－188.

［8］张守玉，封伟书.基于Bootstrap方法的正态分布样本数据生成研究［J］.装配指挥技术学院学报，2009，20 (2):97－100.

(责任编辑 刘舸)

［9］Bradley Efron.Second Thoughts on the Bootstrap［J］.Statistical Science，2003，18(2):135－140.

［10］巩岩，党亚民.基于方差分析周期叠加外推法的电离层TEC短期预报研究［J］.大地测量与地球动力学，2010，30(5):86－89.

(责任编辑 刘舸)

PWM and Analysis of Variance Method in Prediction of Runoff

ZHANG Yun1，YUAN Yong－sheng1，DAI Qi－fan2

(1.College of Science，Hohai University，Nanjing 211100，China;
2.Administrative Office of Irrigation Canals of Jiangsu Province，Huai’an 223200，China)

Prediction of runoff is always an important research topic.Now there have been many prediction models，but they all have their own application conditions.When using periodic extension method based on analysis of variance to predict the runoff，the sample mean is vulnerable to abnormal points based on small sample data.This paper uses the value of PWM to replace the traditional mean value to predict runoff in time series，and contrasts it with the traditional ARMA model.The result shows that PWM and analysis of variance method is feasible，and the error is small.

runoff prediction;analysis in variance;periodic extension;improved PWM method

O212

A

1674－8425(2014)03－0145－03

10.3969/j.issn.1674－8425(z).2014.03.027

2013－10－18

江苏省水利科技创新基金项目(2011059);河海大学自然科学基金资助项目(2009426311)

张云(1989—)，女，硕士研究生，主要从事数理统计及其应用研究;袁永生(1964—)，男，教授，主要从事概率统计及工程中的数学问题研究。

张云，袁永生，戴启璠.径流量预测的PWM方差分析法［J］.重庆理工大学学报:自然科学版，2014(3):145－147.

format:ZHANG Yun，YUAN Yong－sheng，DAI Qi－fan.PWM and Analysis of Variance Method in Prediction of Runoff［J］.Journal of Chongqing University of Technology:Natural Science，2014(3):145－147.