带有食饵避难的Leslie－Gower捕食者－食饵扩散系统的稳定性及最优税收

高 芳，王文爽，王 静

（东北师范大学数学与统计学院，吉林长春130024）

带有食饵避难的Leslie－Gower捕食者－食饵扩散系统的稳定性及最优税收

高 芳，王文爽，王 静

（东北师范大学数学与统计学院，吉林长春130024）

研究了齐次Neumann边界条件下反应扩散对一类食饵具有避难所的Leslie－Gower模型的影响.利用Routh－Hurwitz判别法判断平衡点的局部稳定性，通过构造合适的Lyapunov函数得到了正平衡点全局渐进稳定的充分性条件，根据Pontryagin最大值原理得到了模型的最优税收策略.

Leslie－Gower模型；扩散；平衡点；全避渐进稳定；最优税收

1 预备知识

Leslie－Gower模型和Lotka－Volterra模型是捕食者－食饵系统中两类重要的模型，Leslie－Gower模型体现了环境对捕食者的承载能力与食饵的数量成正相关，同时强调了无论是捕食者还是食饵的增长率都应有一个上限，此模型比一般的Lotka－Voltarra模型更具有实际意义.众所周知，生物资源并非取之不尽，用之不竭的，因此，对其进行最优收获策略方面的研究也就十分必要.但目前，通过控制Leslie－Gower模型的税收，进而控制收获的模型还不多.［1－5］文献［1］考虑了一类食饵具有避难的Leslie－Gower最优税收模型：

并得到了系统（1）的正平衡点的全局渐进稳定的充分条件和其最优税收策略.其中：u，v分别表示食饵和捕食者的种群密度；r1，r2，a2，b1，a，b均为正常数；r1，r2分别为食饵种群和捕食者种群的内禀增长率；a1，a2分别为食饵种群和捕食者种群能够达到的最大平均出生率；b1表示食饵的种间竞争强度；m（0≤m＜1）为食饵的避难率；q表示捕食者种群收获系统；α表示总投入的刚性伸缩系统；E表示对v的收获努力量；p为单位资源v的价格；τ表示单位资源v的税收；c为收获单位资源的成本，采用的收获方式是h（t）＝Eqy，鉴于收获一般是非线性收获，本文采用的收获函数是

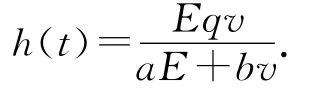
在这里捕食者和食饵密度不是空间依赖的，考虑到捕食者和食饵的数量是不均匀分布的，以及它们对于生存环境的自然生长策略的事实，本文在系统（1）的基础上又引入扩散项，建立了如下模型：

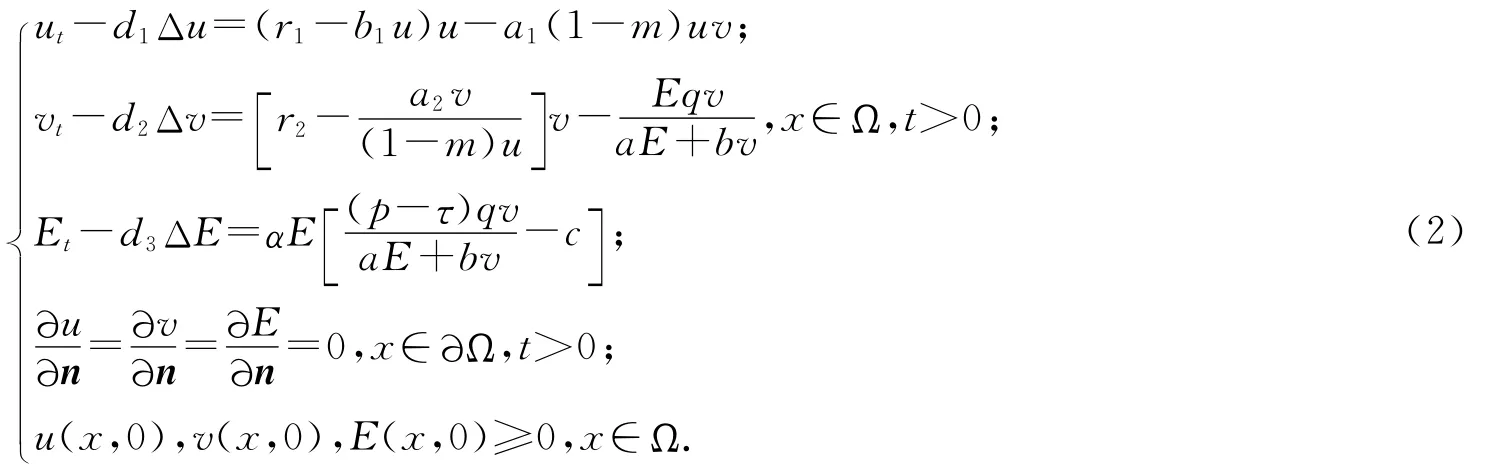
在这里：u，v，r1，r2，a1，a2，b1，a，b，m，q，α，E，p，τ，c与系统（1）具有相同的生物学意义；Δ是拉普拉斯算子；d1，d2，d3为扩散系数；Ω是RN中有界区域，边界∂Ω是光滑的，n是Ω边界上的单位外法向量；

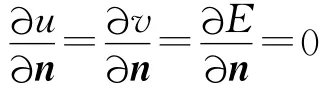
是齐次Numann边界条件，表示环境封闭，物种在边界附近没有迁进迁出.

2 平衡点的分析

经计算，系统（2）有3个平衡点：

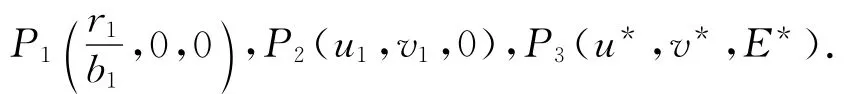
（1）P2（u1，v1，0）满足

解得：

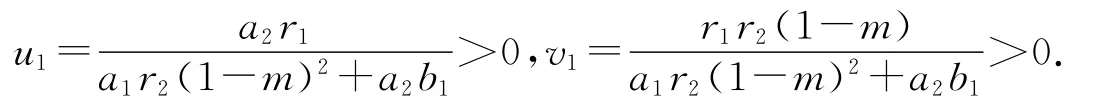
（2）P3（u＊，v＊，E＊）满足

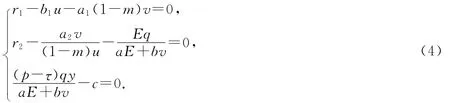
解得：

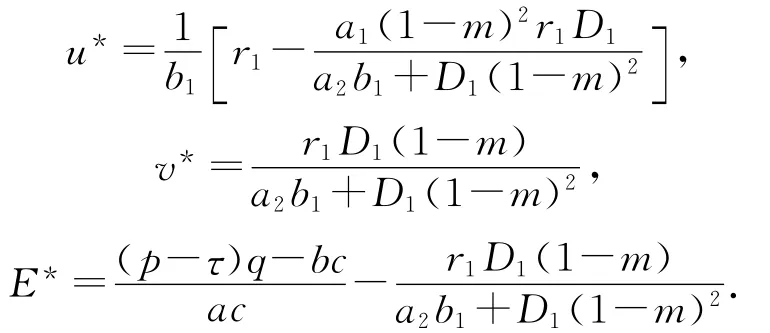
当C＜τ＜max｛A，B｝时，有

则P3（u＊，v＊，E＊）是系统（2）的唯一正平衡点，其中：

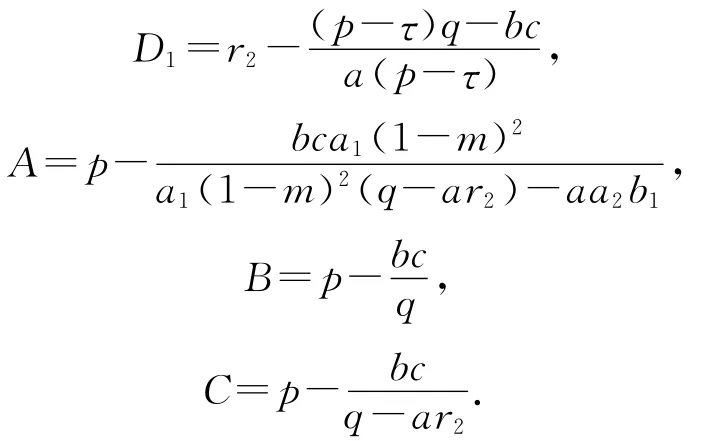
3 稳定性分析

令0＝μ1＜μ2＜μ3＜…是满足Neumann边界条件的在Ω上Δ算子的特征值，E（μi）是μi在C1（Ω）上相应的特征空间，定义集合

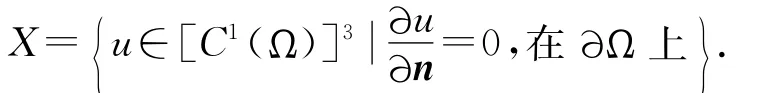
令｛φij，j＝1…dimE（μi）｝是E（μi）的标准正交基，Xij＝｛cφij｜c∈R3｝，则diag（d1，d2，d3），L－DΔ＝J.将（2）式进行线性化，得

其中J为系统（1）的Jacobi矩阵.

注意到：∀i≥1，Xi在算子L下是不变的.这就意味着λ是L在Xi上的特征根，当且仅当λ是矩阵－μiD＋J的特征值.

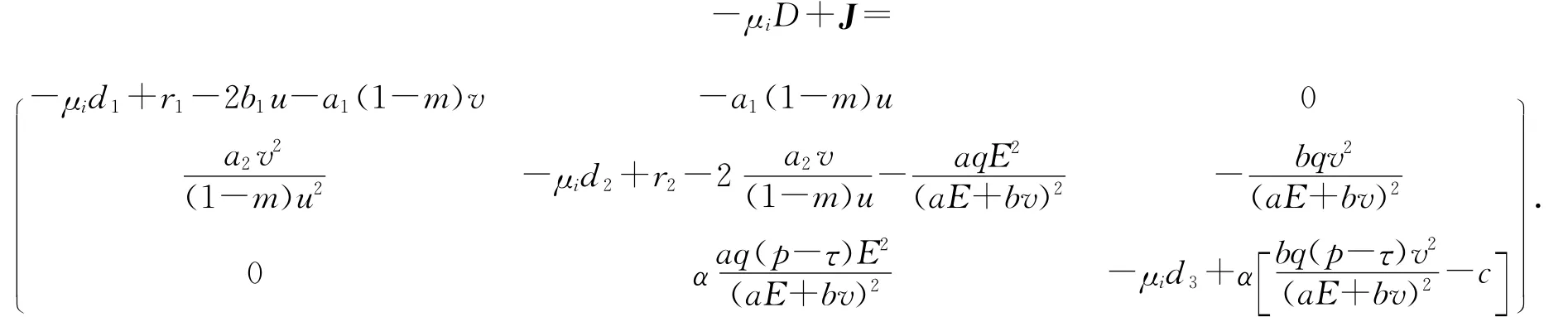
（ⅰ）平衡点P1的稳定性

设平衡点P1处的特征方程为Ψi（λ）＝（λ＋μid1＋r1）（λ＋μid2－r2）（λ＋μid1＋αc）＝0.对于i≥1，Ψi（λ）＝0的三个根记为λi1，λi2，λi3，则有λi1＝－μid1－r1，λi2＝－μid2＋r2，λi3＝－μid1－αc.取i＝1，则λi2＝r2＞0，因此，平衡点P1是不稳定的.

（ⅱ）平衡点P2（u1，v1，0）的稳定性

设平衡点P2（u1，v1，0）处的特征方程为

其中：

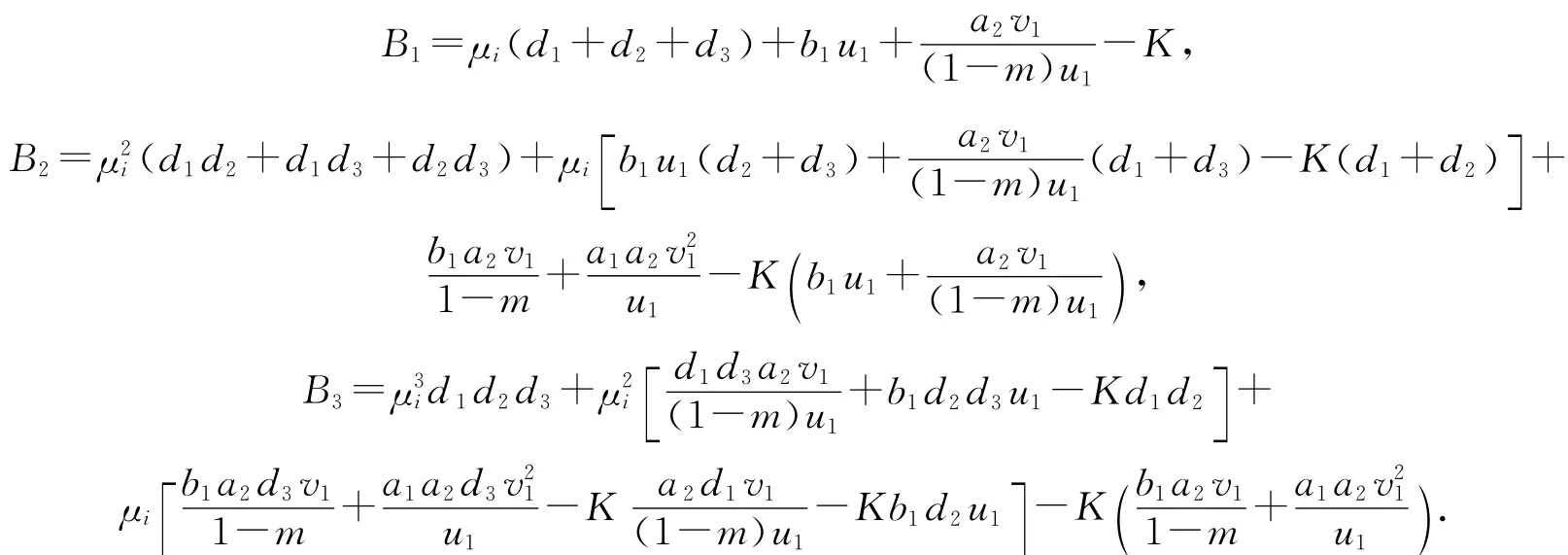
这里

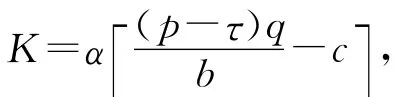
当K＜0时，B1＞0，B2＞0，B3＞0.直接计算能够得到

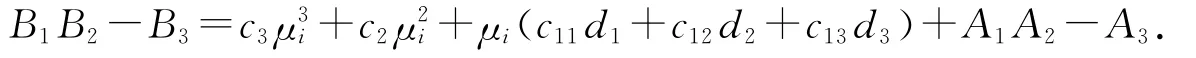
其中：

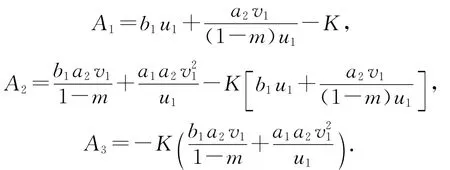
能够验证c3，c2，c11，c12，c13＞0，并且

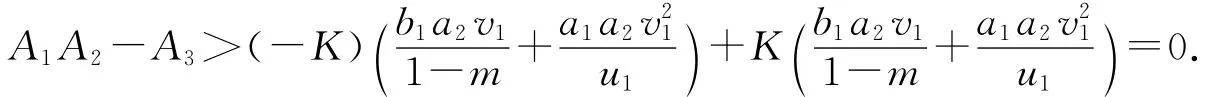
因此，B1B2－B3＞0.根据Routh－Hurwitz判别法可知，对于i≥1，Ψi（λ）＝0的三个根λi1，λi2，λi3均有负实部.

下面，我们证明存在一个正常数δ，使得Reλi1，Reλi2，Reλi3≤－δ，∀i≥1.如果有这个事实成立，就说明由特征值构成的谱存在于Reλ≤－δ内，则平衡点P2（μ1，v1，0）也就是局部渐进稳定的.

令λ＝μiξ，则有

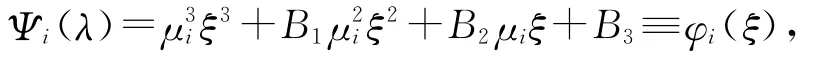
当i→∞时，有μi→∞，

根据Routh－Hurwitz判别法，能够知道φ（ξ）的三个根ξ1，ξ2，ξ3均有负实部，因此存在一个正常数δ′使得Reξ1，Reξ2，Reξ3≤－δ′，根据连续性，我们知道存在i0，使得∀i≥i0，φi（ξ）的三个根ξi1，ξi2，ξi3满足：

∀i≥i0，也就有

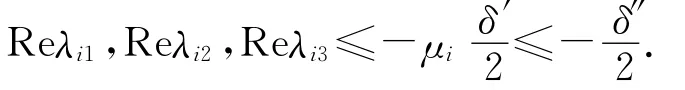
令

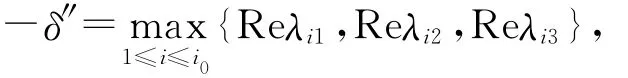
则有

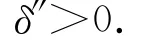
令

则要证的式子成立，平衡点P2（u1，v1，0）也就是局部渐进稳定的.

（ⅲ）平衡点P3（u＊，v＊，E＊）的稳定性

设平衡点P3（u＊，v＊，E＊）处的特征方程为

其中：

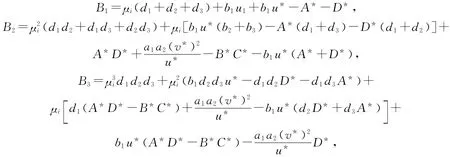
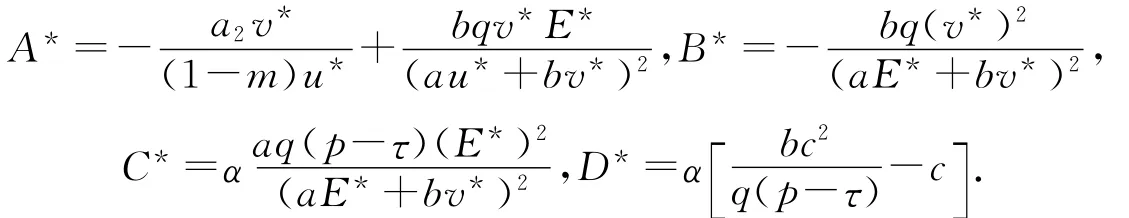
容易看出，B＊＜0，C＊＞0，D＊＜0，因此当A＊＜0，C＜τ＜max｛A，B｝时，有B1＞0，B2＞0，B3＞0.直接计算得到

其中：

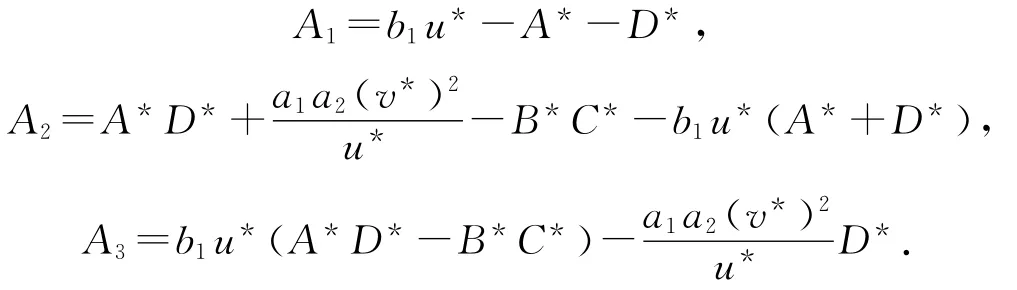
能够验证c3，c2，c11，c13＞0，并且

因此，B1B2－B3＞0.根据Routh－Hurwitz判别法可知，对于i≥1，Ψi（λ）＝0的三个根λi1，λi2，λi3均有负实部.

同平衡点P2（u1，v1，0）的分析一致，存在一个正常数δ，使得

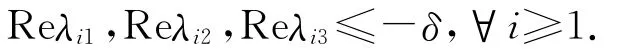
因此平衡点P3（u＊，v＊，E＊）也是局部渐进稳定的.

定理1 若正平衡点P3（u＊，v＊，E＊）存在，则P3（u＊，v＊，E＊）在第一象限直线Au－bv－aE＝0的下半平面内是全局渐进稳定的，其中

证明 取正定函数

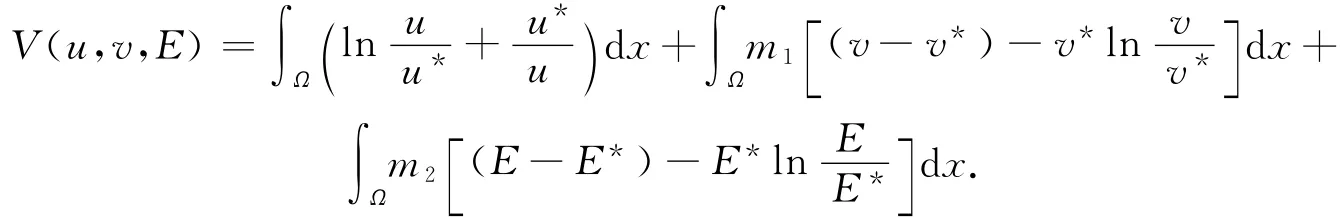
显然，对于任意的u，v，E＞0，V（u，v，E）是连续的.经过计算，可以得到：

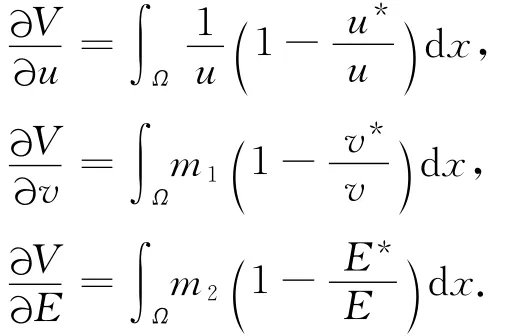
上式表明正平衡点P3（u＊，v＊，E＊）是V（u，v，E）在正的象限内唯一的极值点，所以能很容易地证明

这表明该正平衡点P3（u＊，v＊，E＊）是全局极小值，也就是

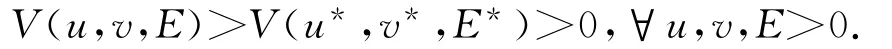
由（4）式得到

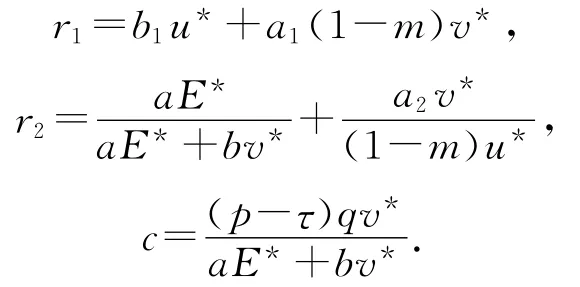
从而有

令

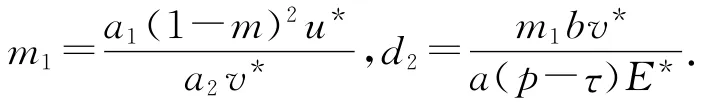
则

当

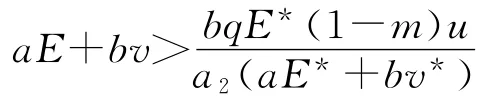
时，有

因此正平衡点P3（u＊，v＊，E＊）在第一象限直线Au－bv－aE＝0的下半平面内是全局渐进稳定的.

4 最优税收政策

我们的目的是通过税收使得系统的社会总收入最大，社会收入的贴现值为

α（t）为贴现因子，一般取α（t）＝e－δt，其中δ为资本贴现率，贴现率又称折现率，指今后收到或支付的款项折算为现值的利率.但是考虑到资本贴现率会随着时间而变化，故在本文中取α（t）＝e－∫′0δ（s）ds，其中δ（t）为资本贴现率，是与时间t有关的函数.

利用Pontrjagin最大值原理找到最优税收政策τ＝τ（t），使得J同时满足系统（2）和控制约束条件τmin≤τ≤τmax时的值最大.该控制问题的Hamilton函数

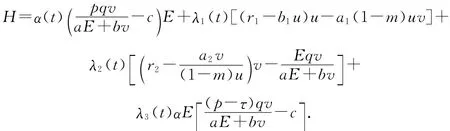
其中：λ1（t），λ2（t），λ3（t）是伴随变量.假设Hamilton函数的最优解不发生在τ＝τmin，τ＝τmax时，我们有

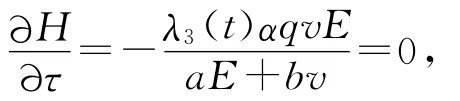
从而λ3（t）＝0.

构造辅助方程式：

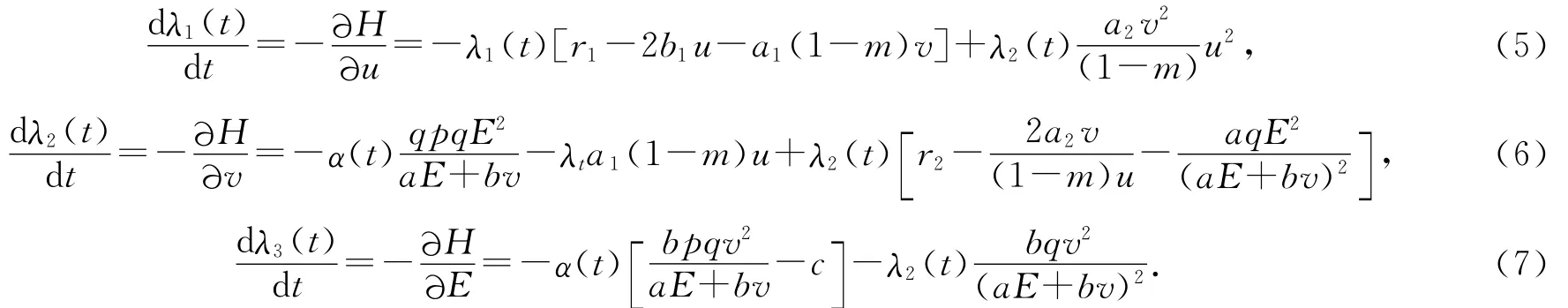
由λ3（t）＝0及（7）式得到

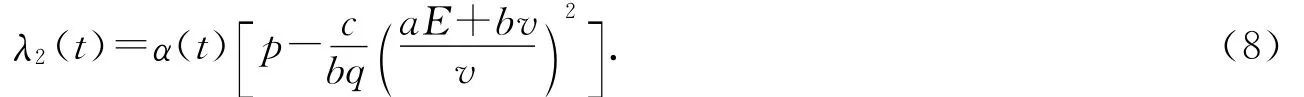
为了得到最优解，在正平衡点P3（u＊，v＊，E＊）处整理方程（5）得到

其中：

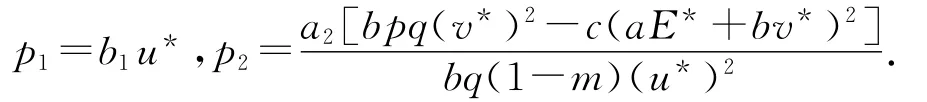
解得

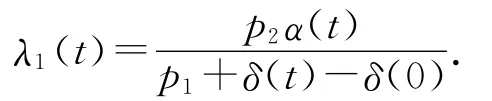
同理得到

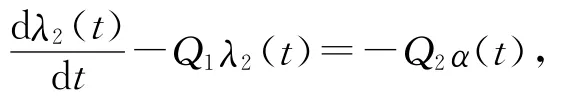
其中：

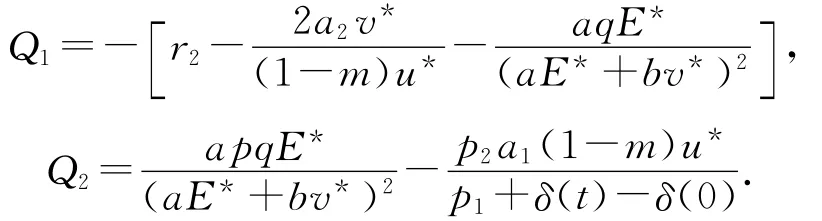
解得

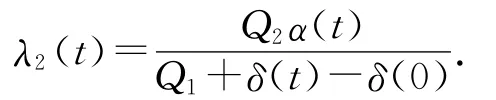
由（8）式得到

将u＊，v＊，E＊代入（9）式得到关于τ的方程，令τδ（t）为方程（9）的解.再将τ＝τδ（t）代入u＊，v＊，E＊，则得到最优平衡解u＝uδ（t），v＝vδ（t），E＝Eδ（t）.

5 结论

通过对一类带有扩散的具有避难所的Leslie－Gower模型的最优税收研究，本文得到了该系统的平衡点及其局部渐进稳定性的充分条件.利用构造合适的Lyapunov函数，进一步得到正平衡点的全局渐进稳定的充分条件.进而由Pontryagain最大值原理得到最优平衡解u＝uδ（t），v＝vδ（t），E＝Eδ（t）.我们的研究结果说明，通过控制税收来控制收获能达到可持续发展和经济效益最大化的双赢结果，有利于资源的合理开发.

［1］ 李有文，杨洪娴，田广立，等.具有食饵避难的Leslie－Gower最优税收模型分析［J］.数学实践与认识，2011，41：167－171.

［2］ 杨斌，王静.具有HollingⅣ型功能性反应的非自治三种群食物链模型的周期解［J］.东北师大学报：自然科学版，2012，44（1）：10－16.

［3］ 柏灵，李晓月，杨帆.捕食－食饵系统的两种群同时捕获的最优化问题［J］.东北师大学报：自然科学版，2001，33（1）：1－5.

［4］ 于新艳，王静.污染环境下具有Beddington－DeAngelis功能性反应的捕食者－食饵系统的动力学行为［J］.东北师大学报：自然科学版，2013，45（1）：6－12.

［5］ 叶其孝，李正元，王明新，等.反应扩散方程引论［M］.第二版.北京：科学出版社，2011：314－340.

Stability and optimal tax of a Leslie－Gower predator－prey model with a prey refuge and diffusion

GAO Fang，WANG Wen－shuang，WANG Jing
（School of Mathematics and Statistics，Northeast Normal University，Changchun 130024，China）

In this paper，we study the stability and optimal tax of Leslie－Gower predator－prey model with a prey refuge and diffusion under the homogeneous Neumann boundary condition.We use the Routh－Hurwitz criterion to prove the local stability of the equilibrium points for the model and by constructing Lyapunov function，sufficient conditions of the globally asymptotic stability of the positive equilibrium for the model are obtained.Finally，the optimal taxation policy of the model is studied by using Pontryagin maximum principle.

Leslie－Gower model；diffusion；equilibrium point；globally asymptotic stability；optimal taxation

O 175.14 ［学科代码］ 110·34

A

（责任编辑：陶 理）

1000－1832（2014）02－0001－08

10.11672／dbsdzk2014－01－001

2013－01－05

国家自然科学基金资助项目（11271065）.

高芳（1987—），女，硕士；通讯作者：王静（1972—），女，博士，副教授，主要从事微分方程和生态数学研究.