一种描述放射性气体模型解的适定性扩展

杨 丽

（潍坊医学院公共卫生学院，山东潍坊261053）

一种描述放射性气体模型解的适定性扩展

杨 丽

（潍坊医学院公共卫生学院，山东潍坊261053）

在新的初值条件下研究了一类双曲与椭圆耦合系统解的适定性，并且将解空间在半群的意义下进行扩展，使此类系统解的适定性有了全新的意义和性质.同时利用该系统解的适定性，使用双曲型伸缩技术，对松弛极限也进行了讨论.

守恒律方程；适定性；半群；松弛极限

1 预备知识

守恒律方程作为偏微分方程的重要组成部分一直是广大数学工作者的重要研究内容，它兴起于20世纪50年代，可以说是一个新的研究领域.它在物理方面的应用非常广泛，几乎所有连续力学的模型都是这种方程.本文的研究对象是一类双曲和椭圆耦合系统的守恒律方程，它是描述放射性气体运动的欧拉方程的简化，系统为［1－4］：

其中：（u，q）（x，t）为未知函数，f（u）是属于C2的光滑函数，初值条件为u（x，0）＝u0（x），f（0）＝0.（x，t）∈（R，［0，＋∞））.方程ut＋f（u）x＋qx＝0是双曲守恒律方程，方程－qxx＋q＋ux＝0是一个线性椭圆方程.这样系统即为双曲－椭圆耦合系统.

下面将方程进行转化［5］，

其中：q＝－Kux，qx＝－Kuxx＝u－Ku，K满足

2 系统适定性已有的结果

考虑原系统转化后的方程

其中f（u）是属于C2的光滑函数，且

上述方程加粘性项后的方程为

其中μ≥0为粘性系数.利用粘性系数消失法，当初始条件u0∈L1（R）∩L∞（R）时，原系统的解具有下列性质：

定理2.1［6－8］设u，¯u∈L∞（［0，T］；L1（R）∩L∞（R））是方程（1.1）的弱熵解，对应初值u0，¯u0∈L1（R）∩L∞（R），则∀t∈［0，T］有

若u0（x）≤¯u0（x），则

且u，¯u∈［－a，a］.其中a＝max｛‖u0‖L∞（R），‖¯u0‖L∞（R）｝.

推论2.1（解的唯一性） 方程（1.1）存在最多一个弱熵解u∈L∞（［0，T］；L1（R）∩L∞（R）），其中对应初值u0∈L1（R）∩L∞（R）.

推论2.2 由解的唯一性知，方程（1.1）的任意熵解u∈L∞（［0，T］；L1（R）∩L∞（R））满足估计式

ω代表初值的L1连续模，且u∈C（［0，T］；L1（R）），其中T＞0.

3 系统适定性的扩展

将初值u0∈L1（R）∩L∞（R）扩展到u0∈L∞（R）.首先赋予新的范数‖｜·｜‖，令

其中φ（x）≥0，φ（x）∈C∞（R），满足

如果定义方程（1.1）的解算子S（t）：t＞0，

这样方程（1.1）的解u（x，t）在初值u0（x）条件下可以表达为

且

总结上述关于方程（1.1）解的一系列性质可以知道解算子S（t）满足下面性质：

（1）S（0）＝I.

（2）S（t＋τ）＝S（t）S（τ），∀t，τ＞0.

（3）如果u0－¯u0∈L1（R），则

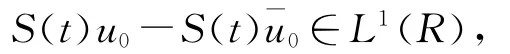
（4）如果u0≥¯u0，∀x∈R，则

（5）S（t）u0∈C（［0，＋∞）；L1（R））.

这样解算子S（t）在空间L1（R）∩L∞（R）中形成了L1的压缩半群，为把这个半群的定义空间扩大至L∞，并且赋予（3.1）式所定义的范数，就需要证明S（t）在空间L1（R）∩L∞（R）中按范数‖｜·｜‖是连续的，为此给出下列定理［9］：

定理3.1 设u，¯u∈L∞（［0，T］；L1（R）∩L∞（R））是方程（1.1）的弱熵解，对应初值u0，¯u0∈L1（R）∩L∞（R），则∀t∈［0，T］，

其中C与φ，‖u0‖L∞，‖¯u0‖L∞有关.

证明 由前面知u，¯u可看做是其粘性逼近方程（2.1）的解uμ，¯uμ的极限，关于（uμ－¯uμ）方程（2.1）两端同乘以检验函数φ，则

类似于定理2.1的证明，在（3.3）式两端同乘以ηε（uμ－¯uμ），其中ηε（ξ）是｜ξ｜的一个正则逼近，从而得到

当ε→0，对x和t进行积分，得到

因为（｜φ′（x）｜＋｜φ″（x）｜）≤C1φ，且由（3.1）式，并应用Gronwall引理，当u↓0时，可以得到（3.2）式.证毕.

在此性质下对于初值u0∈L∞（R）在（3.1）式所定义的范数同样有类似定理2.1的结果.

定理3.2 设u，¯u∈L∞（［0，T］；L1（R）∩L∞（R））是方程（1.1）的弱熵解，对应初值u0，¯u0∈L∞（R），则∀t∈［0，T］有

若u0（x）≤¯u0（x），则

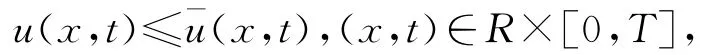
且u，¯u∈［－a，a］，其中a＝max｛‖u0‖L∞（R），‖¯u0‖L∞（R）｝.

4 系统的松弛极限

利用伸缩技术

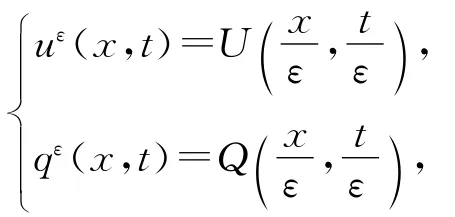
可以把系统

转化为

当ε→0时，由方程组（4.1）的第二个方程知，q＝0时，（4.1）式可以写为

其中f（u）是属于C2的光滑函数，且f（0）＝0.

这样系统的极限方程变为一个双曲守恒律方程式.为了对这一极限过程进行严格的证明，首先对（4.1）式进行改写（类似于预备知识中的变换），得到

对（4.3）式有一系列定理和推论［8］.

定理4.1 设u，¯u∈L∞（［0，T］；L1（R）∩L∞（R））是方程（4.3）的弱熵解，对应初值u0，¯u0∈L1（R）∩L∞（R），则∀t∈［0，T］，有

若u0（x）≤¯u0（x），则

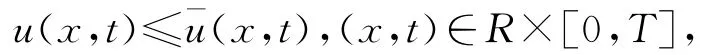
且

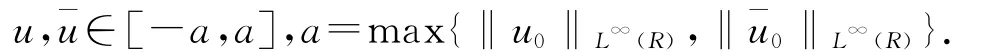
引理4.1 设uε∈L∞（［0，T］；L1（R）∩L∞（R））是方程（4.3）的弱熵解，对应初值u0∈L1（R）∩L∞（R），且

∀h∈R，其中ω（r）→0，r→0，r∈［0，＋∞）.那么，∃C依赖于‖u0‖L∞（R），使得∀t＞0，

由引理4.1的结果知，uε在L∞上一致有界，且在L1Loc是紧的.由此，有下列双曲－双曲型松弛定理：

定理4.2 设uε∈L∞（［0，T］；L1（R）∩L∞（R））是方程（4.3）的弱熵解，对应初值u0∈L1（R）∩L∞（R），那么当ε→0时，∀T＞0，uε→u，在LPLoc（R×［0，T］），P＜＋∞时强收敛，u∈L∞（［0，T］；L1（R）∩L∞（R）），且u是满足方程（4.2）的唯一熵解，对应的初始条件是u0.

［1］ 江泽坚，吴智泉.实变函数论［M］.北京：高等教育出版社，1994：157－159.

［2］ KAWASHIMA S，NISHIBATA S.Shock waves for a model system of a radiating gas［J］.SIAM J Math Anal，1999，17：95－117.

［3］ KAWASHIMA S，NISHIBATA SHOCK S.Cauchy problem for a model system of the radiating gas：weak solutions with a jump and classical solutions［J］.Math Models Methods Appl Sci，1999，62：69－91.

［4］ 杨丽.一类双曲与椭圆耦合系统的适定性和松弛极限［D］.长春：东北师范大学数学与统计学院，2006.

［5］ 杨丽，张毅.一类粘性逼近方程局部解的存在性［J］.临沂师范学院学报，2008，30（3）：19－22.

［6］ KAWASHIMA S.Larger－time behavior of solution stohyperbolic－parabolic system of conservation laws and applications［J］.Proceeding of the Royalsociety of Edinburgh，1987，106（A）：169－199.

［7］ HAMER K.Nonlinear effects on the propagation of sounds waves in a radiating gas［J］.Quarter Journ Mech Appl Math，1971，24：155－168

［8］ KAWASHIMA S，NISHIBATA S.Weak solutions withashockto amodelsystem ofthe radiating gas［J］.Sci Bull Josai Univ，1998，5：119－130.

［9］ NISHIBATA S.Asymptotic behavior of solution stoamodel system of radiating gas with discontinuous initial data［J］.Math Models Methods Appl Sci，2000，10：1209－1231.

The well－posedness extend of a model for radiating gas's solution

YANG Li
（College of Public Health，Weifang Medical University，Weifang 261053，China）

In this paper，the initial condition is considered for a class of hyperbolic and elliptic coupled system well posedness of the solution，and the solution space is extended in the semigroup sense，make the system well posedness of the meaning and nature of the new.At the same time，the well posedness of the solution of this system，the use of hyperbolic type expansion technology，discuss the relaxation limit of the system.

scalar conservation laws；well－posedness；semigroup；relaxation limit

O 175 ［学科代码］ 110·47

A

（责任编辑：陶 理）

1000－1832（2014）02－0012－04

10.11672／dbsdzk2014－02－003

2013－03－31

数学天元基金资助项目（NSFC－11126269）.

杨丽（1979－），女，硕士，讲师，主要从事偏微分方程研究.