一种新的空谱联合稀疏高光谱目标检测方法

宋义刚,吴泽彬,2,3,孙乐,刘建军,韦志辉,3

(1.南京理工大学计算机科学与工程学院,江苏 南京 210094;2.南京理工大学连云港研究院,江苏 连云港 222006; 3.江苏省光谱成像与智能感知重点实验室,江苏 南京 210094)

一种新的空谱联合稀疏高光谱目标检测方法

宋义刚1,吴泽彬1,2,3,孙乐1,刘建军1,韦志辉1,3

(1.南京理工大学计算机科学与工程学院,江苏 南京 210094;2.南京理工大学连云港研究院,江苏 连云港 222006; 3.江苏省光谱成像与智能感知重点实验室,江苏 南京 210094)

目标检测是高光谱数据处理的重要应用之一,高光谱图像中空间和光谱信息的充分利用对于目标检测率的有效提升非常关键。提出一种新的联合稀疏表示的目标检测方法,将混合范数理论和算法应用于高光谱目标检测,在联合高光谱图像空间和光谱信息的基础上,建立了基于联合稀疏性约束的混合范数正则化数学模型,并利用交替方向乘子法对模型进行了优化求解。仿真实验结果表明,该方法能有效提高高光谱目标检测的准确性,降低虚警率。

信息处理技术;高光谱图像;目标检测;混合范数;联合稀疏性;交替方向乘子法

0 引言

高光谱遥感图像具有较高的光谱分辨率,能从可见光到红外光谱区域获取大量非常窄并且光谱连续的遥感图像数据。高光谱图像不仅仅能获得空间维度信息,更重要的是能够获得更精细的光谱维度信息。由于不同地物在不同的波段上的反射率不一样,这就导致不同地物的光谱曲线有所差别,正是这一点使得高光谱数据在地物分类和目标检测方面有着其他数据(如彩色遥感)等所无法比拟的优势。然而,由于高光谱仪器的空间分辨率较低,使得获取到的高光谱数据中纯净的像元很少存在,大部分的像元是以混合形态(即混合像元)存在。混合像元的目标检测和识别是提高遥感应用的关键技术之一。而单纯的从光谱信息出发很难进行混合像元的检测。

目标检测可以看成是一种二类分类问题,其将未知的待检测像元根据其不同的光谱特性分为目标(目标存在)或者背景(目标不存在)。在高光谱目标检测方面,许多学者已经提出了很多的算法[1]。在这些算法中,国际上最常见并被广泛使用的有光谱匹配滤波(SMF)[2-3]、匹配子空间检测器(MSD)[4]和自适应的子空间检测器(ASD)[5].除此之外,支持向量机(SVM)[6-7]在分类方面的广泛应用确定了其在高光谱目标检测方面也具有很好的应用,并得到了很好的检测结果[8]。在国内,高光谱目标检测的研究相对较少,但是也取得了一定的成果。例如,成宝芝等[9]将高光谱解混引入到基于支持向量数据描述(SVDD)算法的异常检测问题中,实现了高光谱图像复杂背景信息和目标信息的分离,得到了很好的检测效果;尹继豪等[10]基于多目标约束能量最小化,以及和约束能量最小化算法提出了一种改进的多个小目标检测算法,取得了很好的检测效果;详细进展可参阅文献[11-13].

稀疏表示理论是近期应用到高光谱目标检测领域的比较新颖的方法[14-15]。它主要基于这一事实:同一类的高光谱像元都近似位于相同的低维子空间中。对于一个未知的待检测像元可以由少数几个训练样本(字典)线性稀疏表示,其稀疏表示的系数就包含有对应的类别信息。为了包含高光谱图像的空间维信息(即相邻的像元属于同一类别的概率较大),联合稀疏性模型被引入到高光谱目标检测中来,其通过同时将待检测目标像元与其相邻像元在相同的训练样本(字典)中进行稀疏表示,使得待检测目标像元与其邻域像元在字典中的稀疏表示系数的支撑集相同,即他们由尽量少的相同的字典原子线性表示。这样,就使得原先无法通过光谱信息进行检测的单一像元,通过结合其邻域像元的光谱分解信息得以确定其究竟是属于目标像元还是背景像元,这就很好地降低了混合像元的检测难度,使得目标检测的结果更精确。基于上述原理,本文提出了联合光谱维信息和空间维信息的联合稀疏表示目标检测模型,并利用交替乘子方向法求解所提出的模型。

1 目标检测稀疏表示模型

式中:Db和Dt分别为背景和目标的训练样本组成的子字典;D则为包含所有类别的训练样本组成的结构化字典;α为待检测像元y在字典D中的稀疏表示系数向量;αb和αt分别为y在背景字典Db和目标字典Dt中的稀疏表示系数向量。这一稀疏向量α可以通过求解下面这一优化问题得到:

式中:‖α‖0表示向量α的非零系数的个数(也称稀疏程度);K0是给定的某一个稀疏程度的上界。问题(2)式是个非确定性多项式(NP)难问题,其精确解很难求得,通常情况下可以通过贪婪算法来近似求解,如正交匹配追踪(OMP)算法。最后,待检测信号y的类别通过比较重构的残差来决定:和

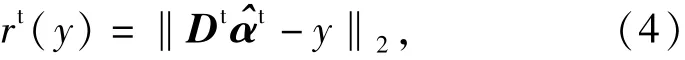
对于预先给定的阈值δ,如果Detector(y)＞δ,那么y被认为是目标,否则,y被认为是背景。

2 空谱联合稀疏目标检测模型

在高光谱图像中,通常相同类别的地物在空间上的分布成聚类特性。即,相邻的地物属于同一类的概率较大。所以,相邻的光谱曲线具有很强的相关性,这一点在高光谱目标识别方面已经得到了验证[15-16]。因此,可以假设相邻像元的光谱曲线在同一字典下的稀疏表示系数具有相同的稀疏模式。设{yt}t=1,2,…,T是以y1为中心像元的空间邻域,那么,

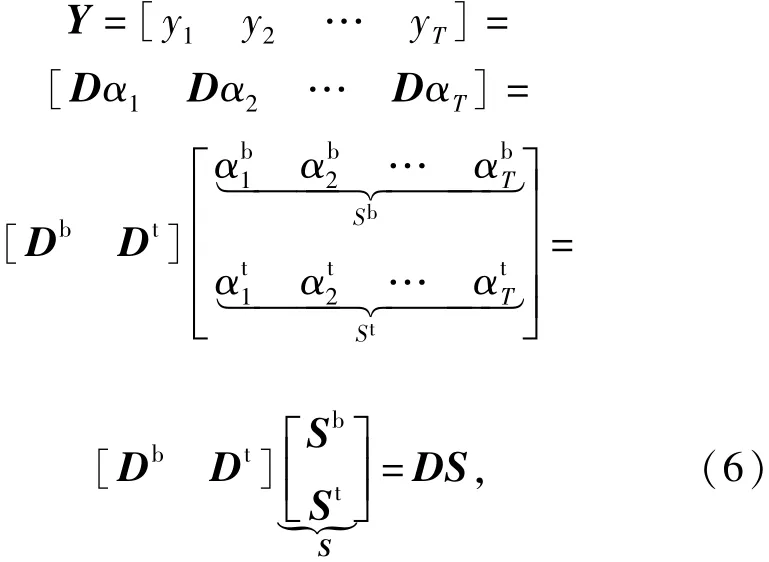
式中:{αt}t=1,2,…,T具有相同的支撑集 Λ,即非零系数所在的行相同。那么,S将是一个行稀疏矩阵,其非零行的个数为|Λ|.S可以通过求解下述优化问题得到:

式中:‖S‖row-0表示矩阵S中非零系数对应的行数。优化问题(7)式是个NP难问题,求解困难,通常用贪婪算法近似求解,如联合正交匹配追踪法(SOMP).为了使问题简化,将问题(7)式松弛为无约束的l1,2混合范数约束的正则化问题,如下:

这一混合范数正则项可以约束稀疏系数矩阵S具有行稀疏性质。在模型(8)式下,最后目标检测的分类器为

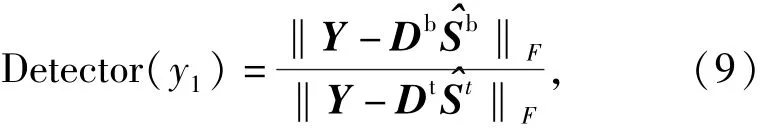
本文利用交替方向乘子法(ADMM)来求解模型(8)式,这一算法被广泛应用于图像处理,压缩感知等领域[17],用来求解类似模型。

通过引入变量V1=DS,V2=S,以及拉格朗日乘子U1和U2,得到模型(8)式的增广拉格朗日方程为

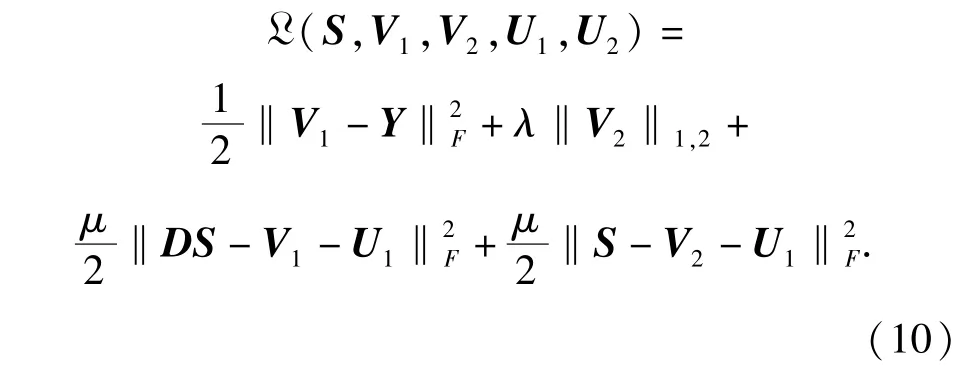
基于ADMM算法的空谱联合稀疏高光谱目标检测算法(l1,2ADMM算法),具体流程如下:

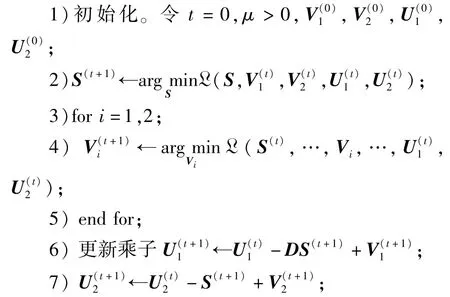
8)迭代次数t=t+1;

9)满足终止条件,输出行稀疏矩阵S,否则,返回2.

l1,2ADMM算法给出了各个变量的求解模型,其中S和V1是个简单的二次规划问题,其解很容易求得。对于变量V2,其对应的优化问题为

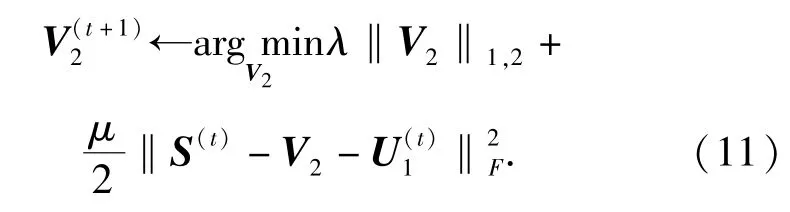
这一问题的解是一个向量软阈值,详见文献[18]。其具体解的形式为

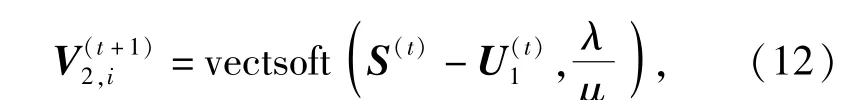
3 仿真实验结果与比较

为了验证所提算法的有效性,共使用两幅高光谱数据进行仿真实验,这两幅图像数据如图1所示,图中显示的是两幅图像第10个波段的灰度图像。

1)第1幅数据为模拟数据。该数据大小为30× 30像素,包含了6个目标,大小分别为3×3像素, 4×4像素和5×5像素各两个,目标排列如图1(a)所示。该图像包含了200个波段的高光谱数据。该图像构成如下:从仿真数据第2幅图像中的所有第9类地物像元中,随机选择100个像元,按照图1(a)中的目标位置进行排列,再从其他剩余的类别地物中随机选择800个像元排列在目标像元周围,构成这一大小为30×30像素的共900个像元的模拟图像数据。

2)第2幅高光谱图像数据采用航空可见/红外成像光谱仪(AVIRIS)于1992年6月采集的高光谱数据集Indian Pines,该数据包含0.2～2.4 μm范围内的220个波段,图像的光谱分辨率为10 nm,空间分辨率为20 m,图像空间维大小为145×145像元,在实验中,去除了20个水汽吸收波段以及信噪比较差的波段,剩余200个有效波段(其第10个波段的灰度图如图1(b)所示)。

图1 仿真实验数据(波段10)Fig.1 Experimental data sets(band 10)

为了进行实验对比,选择了常用的目标检测算法,如匹配滤波(MF)和标记/自适应余弦估计(ACE/S-ACE)[19]、约束能量最小(CEM)和正交子空间投影算法(OSP)[20]、广义的似然测试比算法(GLTR)[21]、混合的非结构检测器(HUD)[22]、自适应的子空间匹配检测器(AMSD)[23],以及最近提出的稀疏表示相关的方法[15-16],如 l1正则化的稀疏表示方法(记作SR)和4-邻域平滑稀疏表示方法(记作SR-S),而本文提出的算法记作l1,2ADMM方法。

为了验证l1,2ADMM算法的有效性,在仿真实验中,首先使用模拟数据进行实验,在该实验中,利用图像左上角的10×10像素共100个像元的光谱作为字典,其中包含背景像元91个,目标像元9个。仿真实验检测结果如图2所示(实验中检测阈值设定为δ=1)。

为了更充分地显示检测结果,将稀疏表示相关的3种检测器的输出进行三维显示,如图3所示。

从模拟数据实验中可以看出,基于稀疏表示理论的高光谱图像目标检测方法较传统的方法具有较大的优势,都能有效地检测到目标的位置,然而在检测的准确性上,原始的稀疏表示模型进行检测的结果较包含空间信息(如本文提出的方法以及SR-S方法)的方法要好,分析原因可能是模拟数据的目标边界过于明显,无法反映出大尺度下遥感数据的邻域信息相互融合的本质。

图2 模拟数据检测结果Fig.2 Detection results on simulated data set

接下来,利用真实的高光谱数据进行算法的有效性验证。IndianPines图像内共包含16种不同的地物,选取第3类地物作为目标,其他类作为背景。在实验中,分别从目标类别中随机选取50个像元构成目标子字典,从背景中随机选取900个像元构成背景子字典。

图3 模拟数据检测器输出的三维显示Fig.3 3-D plots of the Detector outputs on simulated data set

图4给出了所有对比方法在Indian Pines数据集上的实验结果。为了更充分地显示结果,图5给出了SR、本文方法l1,2ADMM以及SR-S三种检测器输出的三维图示。

图6给出了各个算法在真实高光谱数据上的接收机工作特性(ROC)曲线,其中Pd定义为检测到的真实目标像素数目与地面真实目标像素数目的比值;Pf定义为检测到的虚警像素数目同整幅图像像素数目总和的比值。从ROC曲线中可以看出本文算法对高光谱图像目标检测的有效性和准确性是最好的。

图4 Indian Pines图像的各种算法目标检测结果Fig.4 Detection results of different methods on Indian Pines data set

仿真数据实验结果表明,稀疏表示的方法对高光谱目标检测具有很好的效果,而且,原始的稀疏表示方法和4-邻域平滑稀疏表示方法较本文提出的方法在目标检测的准确性上要好,然而真实数据实验表明,本文基于空谱联合稀疏性约束的方法在空间分辨率较低的情况下具有更高的目标检测精度。

图5 SR,l1,2ADMM和SR-S的检测器结果三维显示Fig.5 3-D plots of SR,l1,2ADMM and SR-S detector

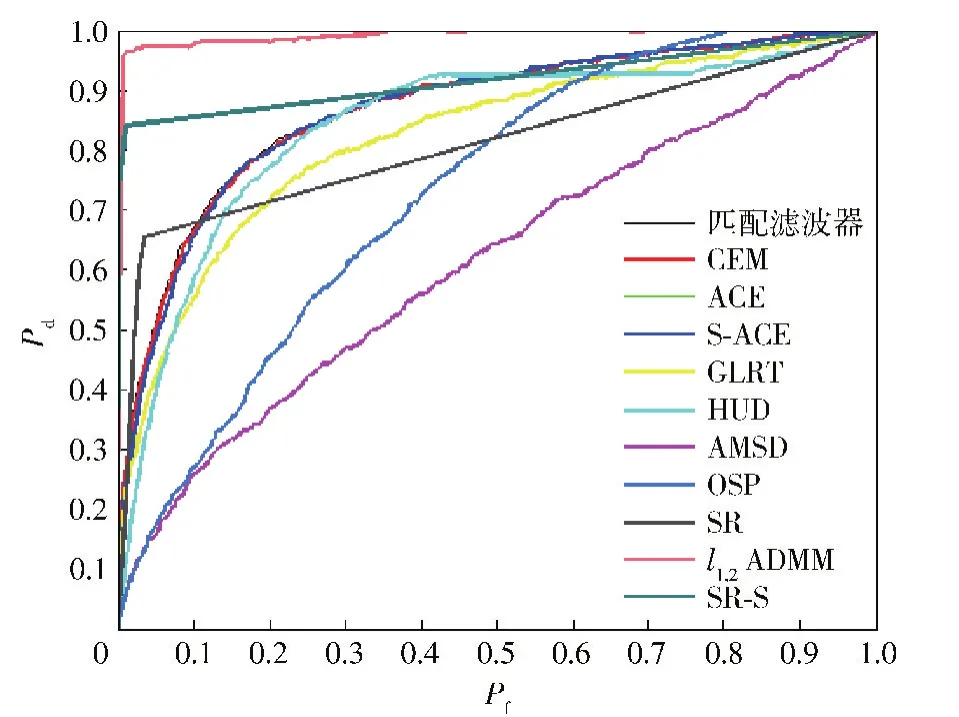
图6 真实高光谱数据实验中各个检测器的ROC曲线对比Fig.6 The ROC curves of different methods on real hyperspectral data set

4 结论

通过对基于混合范数正则化约束的联合稀疏表示模型的研究,建立基于联合稀疏性正则化的高光谱空谱联合的目标检测模型。该模型的建立为光谱维和空间维信息联合进行高光谱目标检测问题的解决提供了一个有效的工具。仿真实验结果表明,本文提出的算法对高光谱图像的目标检测是准确有效的。

References)

[1] Manolakis D,Shaw G.Detection algorithm for hyperspectral imaging applications[J].IEEE Signal Processing Magazine,2002, 19(1):29-43.

[2] Robey F C,Fuhrmann D R,Kelly E J,et al.A CFAR adaptive matched filter detector[J].IEEE Trans on Aerospace and Electronic Systems,1992,28(1):208-216.

[3] Manolakis D,Shaw G,Keshave N.Comparative analysis of hyperspectral adaptive matched filter detectors[J].Proceeding of SPIE Conference on Algorithms for Multispectral,Hyperspectral and Ultraspectral Imagery,2000,4049:2-17.

[4] Scharf L,Friedlander B.Matched subspace detectors[J].IEEE Transactions on Signal Processing,1994,42(8):2146-2157.

[5] Kraut S,Scharf L,McWhorter L T.Adaptive subspace detectors [J].IEEE Transactions on Signal Processing,2001,49(1):1-16.

[6] Boser B E,Guyon I M,Vapnik V N.A training algorithm for optinal margin classifiers[C]∥Proceeding of Fifth Annual Workshop on Computational Learning Theory.New York,US:Association for Computing Machinery,1992:144-152.

[7] Gualtieri J A,Cromp R F.Support vector machines for hyperspectral remote sensing classification[J].Proceeding of SPIE 27th AIRP Workshot:Adavances in Computer Assisted Recognition, 1998,3584:221-232.

[8] Melgani F,Bruzzone L.Classification of hyperspectral remote sensing images with support vector machines[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(8):1778-1790.

[9] 成宝芝,赵春晖,王玉磊.结合光谱解混的高光谱图像异常目标检测SVDD算法[J].应用科学学报,2012,30(1):82-88.

CHENG Bao-zhi,ZHAO Chun-hui,WANG Yu-lei.SVDD algorithm with spectral unmixing for anomaly detection in hyperspectral images[J].Journal of Applied Sciences,2012,30(1):82-88. (in Chinese)

[10] 尹继豪,王艳,王义松.一种改进的高光谱图像中多小目标检测算法[J].电子学报,2010,38(9):1975-1978.

YIN Ji-hao,WANG Yan,WANG Yi-song.A revised multi-target detection approach in hyperspectral image[J].Acta Electronica Sinica,2010,38(9):1975-1978.(in Chinese)

[11] 贺霖,潘泉,邸韚,等.高光谱图像目标检测研究进展[J].电子学报,2009,37(9):2016-2024.

HE Lin,PAN Quan,DI Ge,et al.Research advance on targetdetection for hyperspectral imagery[J].Acta Electronica Sinica, 2009,37(9):2016-2024.(in Chinese)

[12] 赵春晖,胡春梅,石红.采用选择性分段PCA算法的高光谱图像异常检测[J].哈尔滨工程大学学报,2011,32(1):109-113.

ZHAO Chun-hui,HU Chun-mei,SHI Hong.Anomaly detection for a hyperspectral image by using a selective section principal component analysis algorithm[J].Journal of Harbin Engineering University,2011,32(1):109-113.(in Chinese)

[13] 赵春晖,李杰,梅峰.核加权RX高光谱图像异常检测算法[J].红外与毫米波学报,2010,29(5):378-382.

ZHAO Chun-hui,LI Jie,MEI Feng.A kernel weighted RX algorithm for anomaly detection in hyperspectral imagery[J].Journal of Infrared Millimeter Waves,2010,29(5):378-382.(in Chinese)

[14] Chen Y,Nastabadi N M,Tran T D.Simultaneous joint sparsity model for target detection in hyperspectral imagery[J].IEEE Geoscience and Remote Sensing Letters,2011,8(4):676-680.

[15] 赵春晖,李晓慧,朱海峰.空间4-邻域稀疏表示的高光谱图像目标检测[J].哈尔滨工程大学学报,2013,34(9):1171-1178.

ZHAO Chun-hui,LI Xiao-hui,ZHU Hai-feng.Hyperspectral imaging target detection algorithm based on spatial 4 neighborhoods for sparse representation[J].Journal of Harbin Engineering University,2013,34(9):1171-1178.(in Chinese)

[16] Zhao Chunhui,Li Xiaohui,Ren Jinchang,et al.Improved sparse representation using adaptive spatial support for effective target detection in hyperspectral imagery[J].International Journal of Remote Sensing,2013,34(24):8669-8684.

[17] Boyd S,Parikh N,Chu E,et al.Distributed optimization and statistical learning via the alternating direction method of multipliers[J].Foundations and Trends in Machine Learning,2011, 3(1):1-122.

[18] Wright S,Nowak R,Figueiredo M.Sparse reconstruction by separable approximation[J].IEEE Transactions Signal Processing,2009,57(7):2479-2493.

[19] Jin X Y,Paswater S,Cline H.A comparative study of target detection algorithms for hyperspectral imagery[J].Algorithms and Technologies for Multispectral,Hyperspectral,and Ultraspectral Imagery XV,SPIE,2009,7334:73341W1-73341W12.

[20] Qian D,Hsuan R,and Chein-I Cheng.A comparative study of orthogonal subspace projection and constrained energy minimization[J].IEEE Tansactions on Geoscience and Remote Sensing, 2003,41(6):1525-1529.

[21] Ayou B T F,Hainovich A R.Modified GLRT signal detection algorithm[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(3):810-818.

[22] Broadwater J,Chellappa R.Hybrid detectors for subpixel targets [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(11):1891-1903.

[23] Broadwater J,Meth R,Chellappa R.A hybrid algorithms for subpixel detection in hyperspectral imagery[J].IEEE International Geoscience and Remote Sensing Symposium IGARSS, 2004,3:1601-1604.

A Novel Spectral-spatial Sparse Method for Hyperspectral Target Detection

SONG Yi-gang1,WU Ze-bin1,2,3,SUN Le1,LIU Jian-jun1,WEI Zhi-hui1,3
(1.School of Computer Science and Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China; 2.Lianyungang Research Institute of Nanjing University of Science and Technology,Lianyungang 222006,Jiangsu,China; 3.Jiangsu Key Lab of Spectral Imaging and Intelligent Sensing,Nanjing 210094,Jiangsu,China)

Target detection is one of the most important applications of hyperspectral imagery(HSI).The traditional target detection techniques usually discard the spatial information of the target,resulting in a lower accuracy of detection.A novel simultaneous sparse representation model is proposed for HSI target detection.The proposed approach applies the theory and algorithm of mixed-norm to the hyperspectral target detection.By considering the combination of spectral information and spatial context of HSI,a model with a mixed-norm regularizaton based on the simultaneous sparse representation is proposed.And this model is finally solved via alternating direction mehtod of multipliers(ADMM)efficiently.The effectiveness and accuracy of the proposed simultaneous sparse representation model and algorithm are demonstrated by experimental results on a real hyperspectral images.

information processing;hyperspectral imagery;target detection;mixed norm;simultaneous sparsity;altermation direetion mehtod of multipciers?

TG156

A

1000-1093(2014)06-0834-08

10.3969/j.issn.1000-1093.2014.06.013

2013-11-07

国家自然科学基金项目(61101194);江苏省自然科学基金项目(BK2011701);江苏省“六大人才高峰”项目(WLW-011);高等学校博士学科点专项科研基金项目(20113219120024);中国空间技术研究院创新基金项目(CAST201227);中国地质调查局工作项目(1212011120227)

宋义刚(1967—),男,博士研究生。E-mail:songyigang@sina.com;

吴泽彬(1981—),男,副教授,博士。E-mail:wuzb@njust.edu.cn