多故障诊断的即时策略研究

郑致刚,胡云安,吴亮

(1.总参谋部陆航研究所,北京 101121;2.海军航空工程学院,山东 烟台 264001; 3.海军驻合肥地区军事代表室,安徽 合肥 230088)

多故障诊断的即时策略研究

郑致刚1,胡云安2,吴亮3

(1.总参谋部陆航研究所,北京 101121;2.海军航空工程学院,山东 烟台 264001; 3.海军驻合肥地区军事代表室,安徽 合肥 230088)

目前的系统多故障诊断一般是在固定的初始多故障模糊组下预先生成平均测试代价最小的测试序列,然后根据该测试序列建立故障诊断树进行故障定位,因此测试执行顺序和故障诊断树相对固定,当初始多故障模糊组变化后,诊断策略并不能随之灵活地改变。针对这个问题,提出一种多故障诊断的即时策略,推导了多故障模糊组概率计算的迭代公式,通过基于单位代价故障隔离度和信息熵的评估函数选择最佳测试,使用集覆盖的算法寻找后验概率最大的故障单元进行更换或修理。测试案例分析表明:这种即时策略能够灵活地利用已知信息进行多故障定位,具有计算简单、存储空间小的特点,适合复杂系统的多故障诊断。

系统评估与可行性分析;多故障诊断;即时策略;紧集;故障隔离度;信息熵;集覆盖

0 引言

故障诊断技术广泛地应用在工业生产中,特别在可靠性和安全性要求较高的航空、航天和军事领域内更是起着重要作用。故障诊断可以分为系统级和元件级两个层次,故障的定位一般是从系统级到元件级一个逐步细化的过程。目前一种有效的系统级故障诊断方法是Deb等[1]在多信号模型基础上提出的序贯测试方法,该方法通过设计平均测试代价最小的测试序列进行故障单元的定位。Pattipati等[2]使用AO*搜索算法建立最优故障诊断与或树进行故障定位,并成功应用在F-22、UH-60直升机和空间站等复杂系统的故障诊断中。

最初的故障诊断算法大多基于单故障假设,然而随着实际工程系统结构和功能的日趋复杂,单故障假设已经不符合复杂系统故障的实际情况,因此需要研究多故障假设条件下系统的故障诊断问题。Shakeri等[3]在系统单故障诊断的基础上引入更换和修理操作节点,并提出一种多故障诊断的确信策略,该策略的计算复杂度与故障状态的数量m呈指数级关系。Tu等[4]提出一种基本启发搜索算法提高大型系统多故障诊断的实时性。国内对多故障诊断问题也进行了研究[5-7],袁侃等[8]提出一种二元决策图构建的改进规则,建立多故障诊断的决策图,这种方法主要考虑故障概率的影响。方甲永等[9]将系统的多信号模型转化为诊断贝叶斯网络,通过求解约束不等式的最优解实现系统的多故障诊断,该方法需要故障概率统计信息建立故障概率映射。吕晓明等[10]通过构造个体适应度和群体适应度双函数,利用二进制粒子群优化算法求解多故障模糊组的最小碰集,生成多故障诊断策略。

上述多故障诊断策略一般都假定系统初始故障源集合包括所有的组成单元,在此条件下生成完整的故障诊断树,诊断树中每一个节点对应着一个固定的故障模糊组。进行故障诊断时,若系统目前已知的故障模糊组与生成的诊断树中节点表示的故障模糊组都不相同时,则只能从头至尾地执行整个诊断树才能确定故障单元,因此诊断缺乏灵活性。在维修实践中,人们主要考虑的是已知系统当前的故障状态和可用测试集,如何选择下一步的最佳测试,如何根据一系列的测试结果定位故障单元。

针对以上问题,本文提出一种多故障诊断的即时策略,设计了基于单位故障隔离度和单位代价信息熵的评估函数进行最佳测试选择,推导了故障模糊组概率计算的迭代公式,利用集覆盖方法确定故障后验概率最高的单元。这种即时策略的优点在于能够灵活地根据系统目前已知的故障模糊组信息进行测试选择,由于不必产生和存储整个故障诊断树,因此具有计算量小、针对性强的特点,尤其适用于复杂系统的现场交互式排故。

1 多故障诊断问题的相关概念

多故障诊断问题可以用一个5元组(S,P,T,C, B)来定义[3]:

S={s1,…,sm}为系统的可能故障单元集合; P=[p(s1),…,p(sm)]为系统组成单元的故障先验概率向量;

T={t1,…,tn}为系统的可用测试集;

C={c1,c2,…,cn}为测试代价集合,cj是测试tj对应的代价;

B=[bij]为系统的故障单元集合S和测试集合T之间的依赖矩阵,若测试tj能检测到单元si的故障,bij=1,否则bij=0.

在多故障诊断中,为了节省存储空间和计算表示方便,采用紧集[3]的形式表示系统当前的多故障模糊组。多故障模糊组是指能够解释系统目前各种故障表现的故障单元组合的集合。设系统当前多故障模糊组为A,采用紧集形式表示为

式中:X表示多故障模糊组的元素;Fi与G都是系统故障单元集合 S={s0,s1,…,sm}的子集,集合Fi(i=1,…,L)中至少包含1个可能的故障单元,集合G则由系统中已经确定无故障的单元组成。文献[3]中证明,集合F={F1,F2,…FL}的最小碰集就是系统的多故障模糊组。

完整的多故障诊断树一般在系统初始模糊组为A=Θ(1;{s0,s1,…,sm};Φ)情况下开始建立,采用启发式搜索算法生成平均测试代价最小的诊断树,在诊断树的叶节点采取更换或修理操作,排除可能的故障单元后,重新执行未通过的测试,直至定位所有故障单元。在这种故障诊断树中,节点的故障模糊组都是确定的,也就是说只有系统目前的故障状态与诊断树中节点表示的故障状态相同时,才能够从该节点开始继续执行诊断树的操作,否则,都需要从最初的测试节点开始执行,这样在某些情况下产生的诊断策略并非最优,为此本文提出一种多故障即时诊断策略。

2 多故障诊断的即时策略生成

多故障诊断的即时策略根据系统当前的故障状态,采用基于单位代价故障隔离度和信息熵的评估函数选择下一步最佳测试。

2.1 单位代价故障隔离度的评估函数

系统多故障诊断的难度主要由多种故障现象叠加和掩盖造成的,所以测试选择的时候应该首先选择那些故障隔离能力强的测试,尽快确认故障单元后进行更换,不断排除故障单元的干扰后再进行测试,直至定位所有故障。已有的评估函数主要考虑单元的故障概率,本文提出的基本启发函数以故障隔离度高的测试为优选。首先定义单位代价故障隔离度:

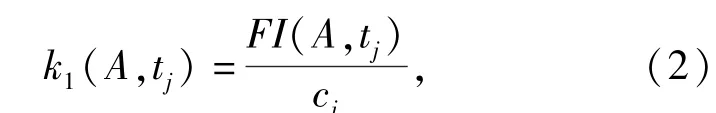
式中:A=Θ(L;F1,F2,…,FL;G)是系统故障状态的紧集表示;FI(A,tj)表示紧集A在测试tj下的故障隔离度,定义为

式中:Ajp和Ajf分别表示紧集A执行测试tj通过和失败两种情况下的紧集;P(Ajp)和P(Ajf)分别表示通过测试tj和未通过测试tj的概率;IR(Ajp)和IR(Ajf)分别表示紧集Ajp和Ajf的故障隔离率。

紧集A的故障隔离率IR(A)的计算为

式中:符号| |表示集合的元素个数,|Gc|表示系统中除已确定故障的单元外可能存在故障的单元数目;N(Fi)表示集合Fi能够隔离故障单元的总数目。由于每个Fi(1≤i≤L)中至少包含1个故障单元,所以如果Fj={sk}(j∈[1,L],k∈[0,m]),则sk必然为故障单元,此时定义N(Fj)=1;如果|Fi|＞1 (i∈[1,L]),集合Fi中必然存在1个故障单元,只是不能确定具体的故障单元,此时定义:

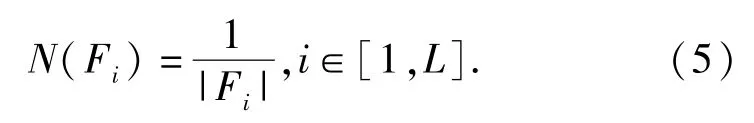
对于紧集A=Θ(L;F1,F2,…,FL;G)来说,它能够隔离的故障单元数目根据(6)式计算:

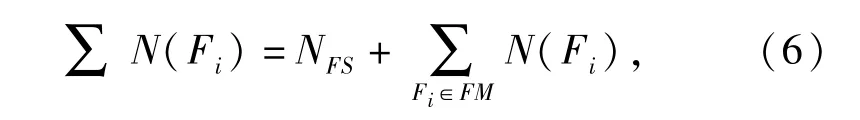
式中:NFS表示Fi(1≤i≤L)中单元素集合的总数; FM表示其中元素个数大于1的集合。

2.2 单位代价信息熵的评估函数

基于单位代价故障隔离度的评估函数作为测试选择的首要标准,当两个测试的评估函数值相等时,采用传统的单位代价信息熵函数对测试进行评估。设系统目前的可用测试集为T={t1,t2,…,tn},考虑执行T中的每个测试后得到的信息熵变化,选择测试集T中能够最大化单位代价信息熵k2的测试tk.单位代价信息熵k2根据(7)式计算:

式中:A为当前时刻多故障模糊组;IG(A,tj)表示测试tj的信息熵,

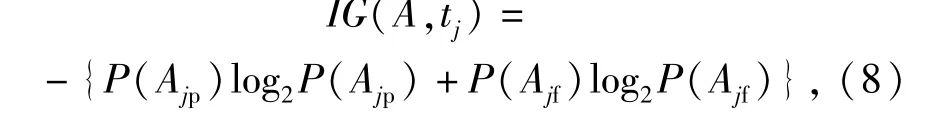
(8)式中相关符号的表示意义与(3)式相同。

以上给出了测试选择的2个评估函数,在计算这2个评估函数值的时候都要计算条件概率P(Ajp)和P(Ajf),下面给出它们的迭代计算公式。

2.3 多故障模糊组条件概率的迭代计算

设系统目前的多故障故障模糊组A的紧集表示为

执行测试tj后,若通过测试tj,系统的多故障模糊组为Ajp;若测试tj失败,系统的多故障模糊组为Ajf.根据紧集的性质[3],Ajp与Ajf分别为

从(18)式和(19)式可以看出:在非冗余系统中,执行测试tj后,系统的多故障模糊组概率P(Ajp)或P(Ajf)可以通过测试前系统多故障模糊组的概率P(A)计算。换句话说,系统每一时刻的故障概率可以使用以前时刻的故障概率迭代计算得到,这样不必每步都通过计算集合F={F1,F2,…,FL}的最小碰集得到模糊组的故障概率,从而在一定程度上提高了计算效率。

2.4 故障单元的更换和修理

在多故障诊断中,计算当前可用测试集中每个测试的评估函数,选择执行评估函数值最大的测试,然后在可用测试集中删除已经执行的测试,继续下一步的测试选择。重复上述过程,最后可能得到两种结果:1)定位至少一个故障单元;2)可用测试已经不能提供进一步的故障信息。对于第1种情况,将确定故障的单元进行更换或修理,然后该单元从F中删除并加入集合G,如果所有的Fi都删掉,那么此时的多故障模糊集A=Θ(1;F1=S-G;G),更新测试集合T,继续进行测试。对于第2种情况,可以将所有可能的故障单元全部进行更换或修理,或者采取顺序更换的办法,更换的顺序按照故障后验概率的大小进行,即已知通过的测试集Tp和失败的测试集Tf情况下,确定可疑故障集X⊆S,使其后验概率Prob(X|Tp,Tf)最大。

根据贝叶斯理论:

在已知Tp和Tf情况下,Prob(Tp,Tf)等于常量,所以最大值由Prob(Tp,Tf|X)Prob(X)决定,由于

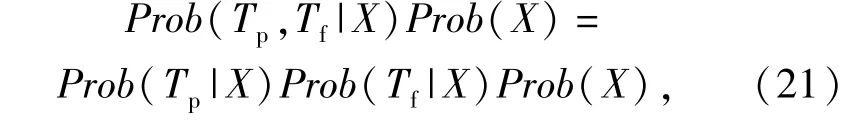
设si∈X时xi=1,si∉X时xi=0,则

文献[4]证明多故障诊断问题可以归纳为集合覆盖问题,即

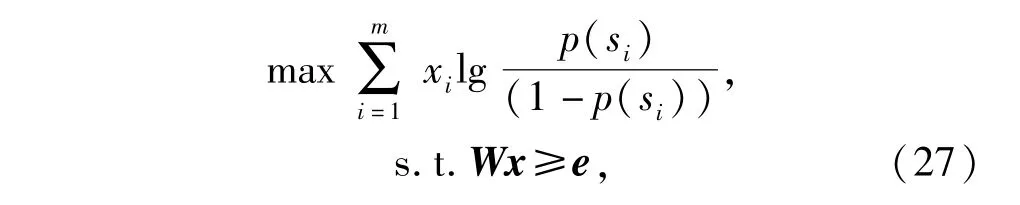
式中:x=[x1,x2,…,xL]T,xi∈{0,1};W为故障依赖矩阵中所有未通过的测试Tf组成的m×|Tf|矩阵;e为单位列向量。

传统的集覆盖问题是整数规划的非确定性多项式(NP)完全问题,当故障依赖矩阵D的维数过大时无法在多项式时间内得到最优解,此时只能采用启发式算法得到近优解。本文使用文献[4]中的算法寻找后验概率最大的多故障解,具体求解过程参考文献[11].在故障依赖矩阵规模较大时,该算法能够快速求出最可能的多故障解。

3 应用举例

本文选用一个常用的典型系统[3]进行多故障诊断的即时策略分析,系统的故障依赖矩阵如表1所示。使用扩展单故障的多故障诊断方法[3]生成的诊断树如图1所示。

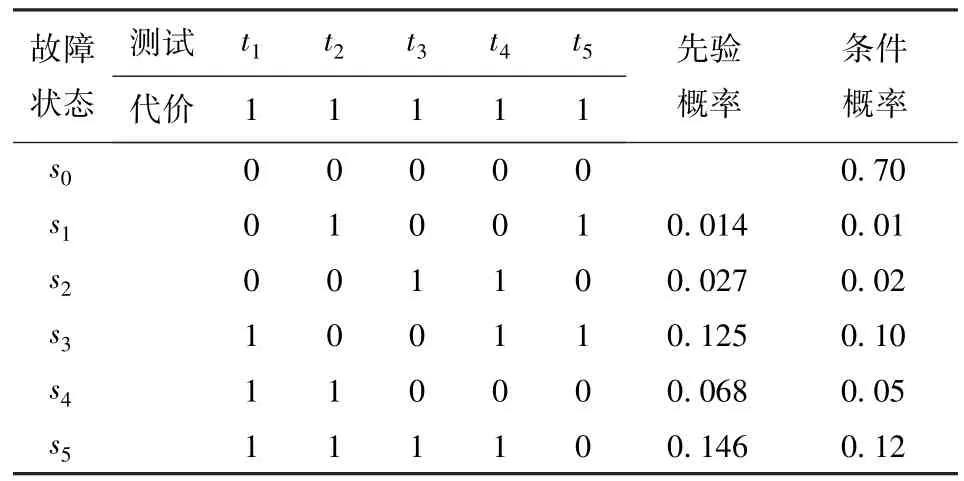
表1 故障依赖矩阵Tab.1 Fault dependency matrix

上述诊断策略是在系统故障状态全部未知情况下的故障诊断树。当系统已知状态与诊断树中或节点相同时,可以从该节点开始进行测试,否则需要从头开始执行整个诊断树。假设系统故障诊断前经过串换件已确定系统的初始多故障模糊组为B= Θ(2;{s3,s4,s5},{s2,s3,s5};φ),这个多故障模糊组与图1诊断树中的或节点不同,该诊断树并不能给出当前的最佳测试,此时可以使用本文的即时策略进行故障定位。

根据目前故障状态测试t1和t4已经没有必要进行,只需在t2、t3和t5中选择下一步测试,下面分别计算每个测试的启发评估函数。

图1 扩展单故障的多故障诊断树Fig.1 Multiple fault diagnosis tree of extended single fault

根据计算结果选择最优测试t2.类似地,根据不同的测试结果选择下一步测试,直至测试集不能提供进一步的故障信息,结果如图2所示。

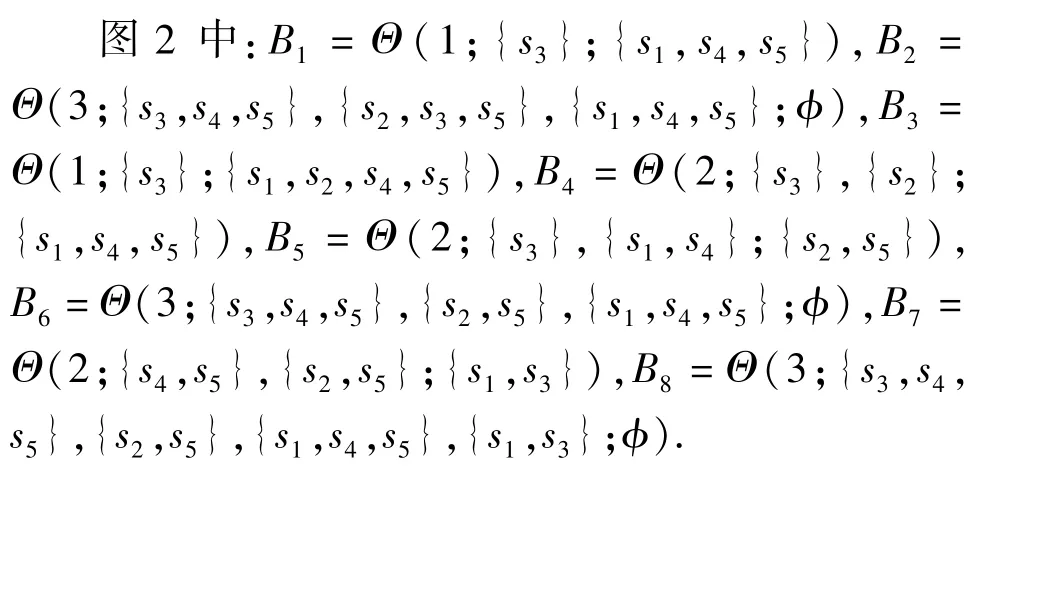
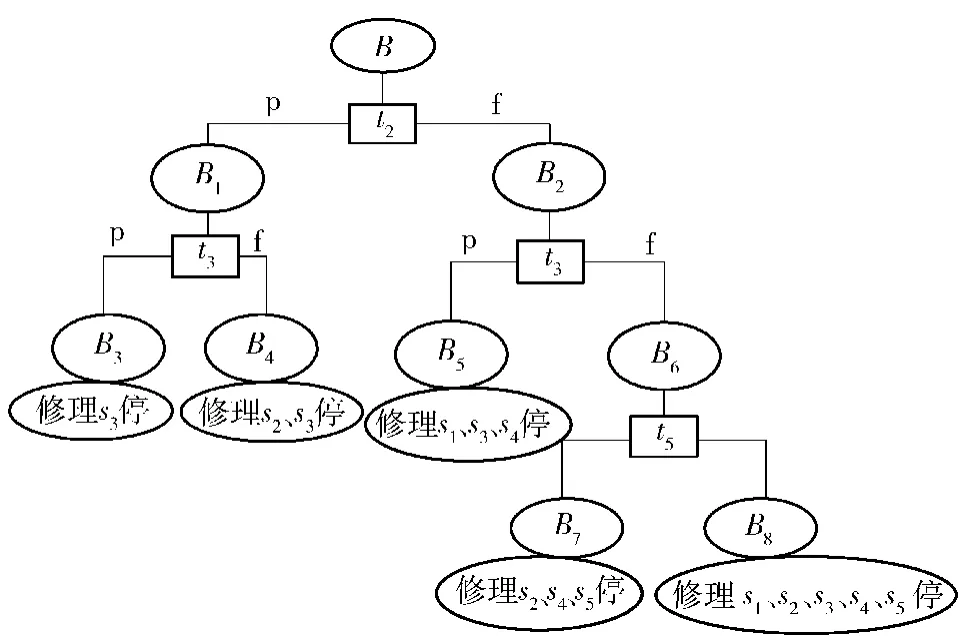
图2 即时策略的多故障诊断树Fig.2 Multiple fault diagnosis tree of on-line strategy

使用集覆盖方法可得在状态B7时s5故障的后验概率最大,状态B8时s5和s3故障的后验概率最大,因此首先更换或修理这些单元,然后继续测试。

从例子可以看出,这种多故障诊断即时策略可以直接根据系统当前的故障状态给出目前的最佳测试,简化了测试步骤,同时能够充分利用测试集提供的信息,确定系统的故障状态和故障单元更换的先后顺序。即时策略的每一步测试都是在线计算选择的,所以不必存储多余的节点信息,迭代算法也节省了计算资源,因此这种方法尤其适合应用在系统故障状态较多且计算资源有限的情况。目前这种多故障定位的即时策略生成算法已经应用在某型直升机便携式外场辅助维修系统的诊断软件中,通过与外场机务人员的交互,给出测试建议,实现故障单元的快速定位。

4 结论

本文主要研究多故障情况下即时诊断策略的生成,提出了基于单位代价故障隔离度和信息熵的评估函数进行最佳测试选择,通过集覆盖的算法确定故障后验概率最大的故障元件进行修理或更换。这种即时诊断策略充分利用测试集提供的信息,将领域知识与故障概率以及测试代价相结合,能够在任意初始故障模糊组的情况下选择最佳测试,与固定的故障诊断策略相比更具灵活性。本方法没有考虑系统存在冗余的情况,并且假定每次测试都是准确的,但实际中由于噪声干扰或时间延迟等原因会出现不可靠测试,今后将进一步研究存在系统冗余和测试干扰情况的多故障诊断策略。

References)

[1] Deb S,Pattipati K R,Raghavan V,et al.Multi-signal flow graphs:a novel approach for system testability analysis and fault diagnosis[J].IEEE Aerospace and Electronic System Magazine, 1995,10(5):14-25.

[2] Raghavan V,Shakeri M,Pattipati K R.Optimal and near-optimal test sequencing algorithms with realistic test models[J].IEEE Transaction on Systems,Man and Cybernetics,1999,29(1): 11-26.

[3] Shakeri M,Raghavan V,Pattipati K R,et al.Sequential testing algorithms for multiple fault diagnosis[J].IEEE Transactions on Systems,Man and Cybernetics,2000,30(1):1-14.

[4] Tu Fang,Pattipati K R,Deb S,et al.Computationally efficient algorithms for multiple fault diagnosis in large graph based systems [J].IEEE Transactions on Systems,Man and Cybernetics,2003, 33(1):73-85.

[5] 杨鹏,邱静,刘冠军.多故障诊断策略优化生成技术研究[J].兵工学报,2008,29(11):1379-1383.

YANG Peng,QIU Jing,LIU Guan-jun.Research on optimization generation technology for multiple fault diagnostic strategy[J]. Acta Armamentarii,2008,29(11):1379-1383.(in Chinese)

[6] 王子玲,许爱强,林雪原,等.一种冗余系统诊断策略优化设计算法[J].海军航空工程学院学报,2013,28(5):539-542.

WANG Zi-ling,XU Ai-qiang,LIN Xue-yuan,et al.An optimal design algorithm of redundant system diagnostic strategy[J].Journal of Naval Aeronautical and Astronautical University,2013,28(5): 539-542.(in Chinese)

[7] 李宝晨,黄考利,连光耀,等.基于BQPSO的多故障最小候选集生成技术研究[J].计算机测量与控制,2013,21(6):1476-1479.

LI Bao-chen,HUANG Kao-li,LIAN Guang-yao,et al.Study on generation of a multiple fault minimal candidates set based on BQPSO[J].Computer Measurement&Control,2013,21(6): 1476-1479.(in Chinese)

[8] 袁侃,胡寿松.一种用于多故障诊断的改进二元决策图算法[J].控制与决策,2010,25(7):1117-1120. YUAN Kan,HU Shou-song.Enhanced BDD algorithm for multiplefault diagnosis[J].Control and Decision,2010,25(7):1117-1120.(in Chinese)

[9] 方甲永,肖明清,王学奇,等.测试不可靠条件下多故障诊断方法[J].北京航空航天大学学报,2011,37(4):433-438.

FANG Jia-yong,XIAO Ming-qing,WANG Xue-qi,et al.Multiple fault diagnosis method with unreliable test[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(4): 433-438.(in Chinese)

[10] 吕晓明,黄考利,连光耀.基于BPSO的多故障最小候选集生成技术[J].系统工程与电子技术,2012,34(5):961-965.

LYU Xiao-ming,HUANG Kao-li,LIAN Guang-yao.Generation of minimal candidate set for multiple fault diagnosis based on binary particle swarm optimization[J].Systems Engineering and E-lectronics,2012,34(5):961-965.(in Chinese)

[11] 刘磊,龙兵,刘震.两种多故障诊断算法的性能比较研究[J].电子测量与仪器学报,2011,25(1):75-80.

LIU Lei,LONG Bing,LIU Zhen.Research on performance comparison of two MFD algorithms[J].Journal of Electronic Measurement and Instrument.2011,25(1):75-80.(in Chinese)

Study of on-line Diagnosis Strategy for Multiple faults

ZHENG Zhi-gang1,HU Yun-an2,WU Liang3
(1.Army Aviation Research Institute,Beijing 101121,China;
2.Naval Aeronautical and Astronautical University,Yantai 264001,Shandong,China; 3.Military Representative Office of Navy in Hefei,Hefei 230088,Anhui,China)

The present system multiple fault diagnosis is generally realized by generating a test sequence with minimal average test cost under fixed initial fault ambiguous groups,and then the faults are isolated through the fault diagnosis tree constructed according to the generated test sequence,so the test sequence and fault diagnosis tree are relatively fixed.When the initial faults ambiguous groups change,the test strategy still keep unchanging.To resolve the problem,an on-line strategy for multiple fault diagnosis is proposed,the iterative formulas to calculate the possibility of ambiguity groups are deduced,and the optimal test is selected by evaluation function based on fault isolation degree and information entropy of unit cost.The faulty unit with highest posterior possibility to be repaired is searched by set covering algorithm.Test case shows that the on-line strategy can isolate multiple faults by flexibly utilizing known information.It has the advantages of simple calculation and small storage space,and is feasible for multiple fault diagnosis of complex system.

system assessment and feasibility analysis;multiple fault diagnosis;on-line strategy;compact set;fault isolation degree;information entropy;set covering

TP39

A

1000-1093(2014)06-0921-06

10.3969/j.issn.1000-1093.2014.06.025