典型弹道下的火箭弹MEMS-INS/GNSS 组合导航姿态误差可观性分析

董进龙，莫波

(北京理工大学 宇航学院，北京100081)

0 引言

微机电系统(MEMS)惯性器件具有价格低廉、使用简单以及抗过载能力强的优点，因此被广泛应用在低成本的弹药系统中。但是，由于精度偏低、零偏稳定性较差、对环境的敏感度较大，使MEMS 器件在纯惯性导航系统(INS)中的应用受到很大的限制。随着常规弹药的制导化，MEMS-INS 成为首选的弹上测姿系统，如果与全球导航卫星系统(GNSS)构成组合导航系统，形成优势互补，则能够实现常规无控弹药的低成本制导化。

MEMS-INS 与GNSS 这种优势互补需要一个前提条件:组合导航系统的状态必须是可观的。只有满足这个条件，才能够利用组合导航系统估计出相应的偏差，并进行补偿。因此，分析MEMS-INS/GNSS 组合导航系统在不同条件下的最优估计性能，能够有效地指导组合导航系统的最优设计。

当前，线性系统的可观性分析有多种方法。对于非随机系统，一般根据系统的可观性矩阵或者系统的Gramian 矩阵的特性来判断系统是否完全可观。基于此类原理发展出了:基于可观性矩阵或Gramian 矩阵的特征值以及特征向量来判断状态的可观性［1］;对于线性时变系统，利用分段线性定常系统(PWCS)原理，通过系统总可观性矩阵(TOM)或者提取可观性矩阵(SOM)，来分析系统在整个时间段上的可观性［2］，或者采用简化的方法，分析系统在特定时间段上的局部可观性［3］;将可观性矩阵进行奇异值分解，然后根据奇异值的大小来判断相应状态的可观性［4-6］。施桂国等［7］利用奇异值法对巡航导弹的惯性/地磁匹配组合导航系统进行了可观性分析。文献［8 -9］则在上述方法基础上将系统在特定时段内看作定常系统，分析系统的局部可观性，并在奇异值方法的基础上定义了可观性矩阵的条件数来进一步表征系统的可观测程度。相对于系统在整个时域上的可观性，文献［10 -12］则在瞬时可观性概念的基础上，具体分析了捷联惯导系统(SINS)/全球定位系统(GPS)组合导航系统在不同机动情况下的可观性。

另外，还可以利用随机系统可观性分析方法来判断系统的可观性，其中包括:以系统状态误差方差阵为研究对象，计算矩阵的特征值和特征向量，然后根据特征值的大小以及特征向量来判断相应状态的随机可观测程度［13-14］;此外，利用系统矩阵和噪声协方差矩阵构成随机系统的Riccati 方程，然后根据噪声方差有界原则，来判断状态的可观性［15］。而文献［16］则利用系统初始的误差协方差矩阵和系统矩阵构成协方差矩阵，将其进行奇异值分解，来分析系统在各个子空间上的可观性。

有一部分学者利用系统矩阵的特征值、特征向量以及测量矩阵构成系统的可观性因子，用于分析系统各个状态的可观性。

对于非线性系统，利用局部线性化的方法，分析系统的线性可观性。针对某些特定的非线性系统，例如INS-GPS 组合导航系统，一些学者从系统可观性的定义出发，结合特定的工作条件，来分析系统的全局可观性［17］。

本文考虑到噪声特性对最优估计的影响也是通过系统结构进行传播的，因此，暂不考虑系统噪声的影响，以远程制导火箭弹为研究对象，建立了MEMS-INS/GNSS 松组合系统。利用线性系统的可观性分析方法，分析了火箭弹的姿态误差在3 种典型弹道下的可观性，并通过仿真验证结果的正确性。

1 MEMS-INS/GNSS 反馈式松组合导航系统的建立

采用最常用的INS/GNSS 松组合系统结构，建立具有15 个偏差状态的卡尔曼滤波(KF)系统［18］，状态变量选取如下:

由于MEMS-INS 系统的惯性器件精度较低，其姿态、速度以及位置误差会迅速发散，因此，有必要采用反馈式组合导航结构，定期对惯导的姿态误差、导航误差以及传感器误差进行修正，以确保短时间内惯导独立工作的精度，同时，也能够有效地抑制由于滤波器状态增大而引起的截断误差和系统建模误差，防止滤波发散。反馈滤波系统的结构如图1 所示。

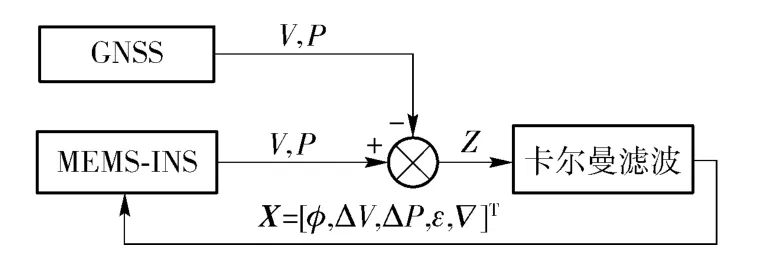
图1 具有状态反馈结构的卡尔曼滤波系统Fig.1 Kalman Filter system with state feedback

离散系统基本KF 方程如(1)式所示，

根据最优估计理论以及反馈系统原理，卡尔曼滤波器输出的最优估计值在反馈到MEMS-INS 系统之后，在进行下一次滤波计算之前，应该将滤波器状态置为0，以保证卡尔曼滤波器的最优性。因此，具有MEMS-INS 状态反馈结构的MEMS-INS/GNSS 组合导航KF 系统方程如(2)式所示，

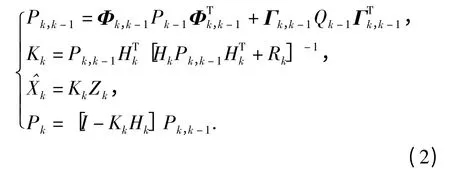
从理论上来讲，反馈式KF 更能符合误差为小量的假设，滤波性能要优于输出校正KF. 但是，在工程应用中，实际系统都是离散时变系统，滤波结果会受到滤波步长以及滤波时刻系统模型的精度影响，滤波偏差必然存在。对于状态反馈式KF 组合导航系统，错误的滤波结果会直接传播到惯导系统中，在最坏情况下，会使闭环回路不再满足负反馈的条件，导致系统发散。而输出校正式KF 的滤波结果不会直接影响惯导系统，系统建模误差就不会传播到惯导系统中。因此，从这上述观点出发，当系统建模误差较大时，输出校正式KF 往往比反馈式KF更加可靠。实际上，造成上述问题的原因主要有以下两点:

1)离散时变系统在滤波时刻的系统矩阵Φk，k+1只能代表当前时刻的系统参数，如果系统参数在两个时刻之间出现了短时突变(如飞行器的短时机动)，滤波系统的模型与实际系统就出现了差异，从而使最优估计出现误差;

2)当某些系统状态的可观性较差时，这些状态的最优估计结果就会在很大程度上取决于模型中的噪声特性以及建模误差，当噪声模型与实际噪声特性存在较大误差时，不可观状态的最优估计结果就会存在较大的误差。

因此，对于离散时变系统，在应用状态反馈式KF 时，应合理选择滤波步长，同时，有必要分析无噪声系统的可观性，根据状态可观性分析结果，适当的改变反馈结构，只反馈那些可观性好的状态，保证反馈系统的稳定性。

2 火箭弹组合导航系统可观性分析

2.1 系统可观测性分析的奇异值分解法

对于离散时变线性系统，采用PWCS 原理，将系统进行适当的分段处理，计算每个段上的系统可观性矩阵，这样就能够得到系统的总观测性矩阵，从而得到每个时刻的系统状态的可观性。下面介绍一种基于系统可观性矩阵的奇异值分解的可观性分析方法。

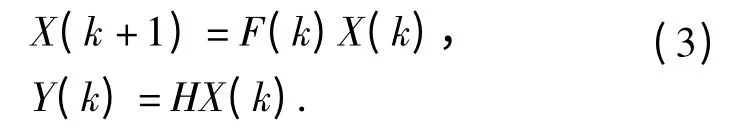
系统状态X(k)的维数为n，观测量Y(k)的维数为m，系统的可观性矩阵为

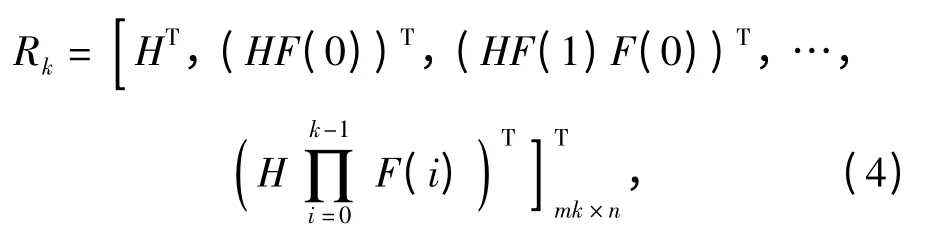
则有

式中:Y 表示从零时刻开始所有的观测值组成的mk维列向量，Rk的奇异值分解可表示为

式中:U =［u1，u2，…，umk］是mk ×mk 维正交矩阵;V=［v1，v2，…，vn］是n × n 维正交矩阵;Σ =是mk × n 阶矩 阵，其 中，S =diag(σ1，σ2，…，σn)是Rk的奇异值与0 组成的对角矩阵，σ1≥σ2≥…≥σr＞σr+1=…=σn=0，其中，大于0 的σi为Rk的奇异值。将(6)式代入(5)式并进行变换得

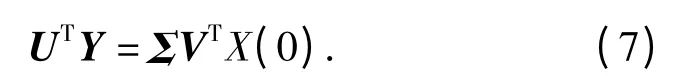
设Y' =UTY，X'(0)=VTX(0)，分别表示观测量和初始状态的单位正交变换，则有

可见，可观性矩阵的奇异值实际上表征了初始状态到测量输出的传递增益。将(8)式写成标量形式如(9)式所示:

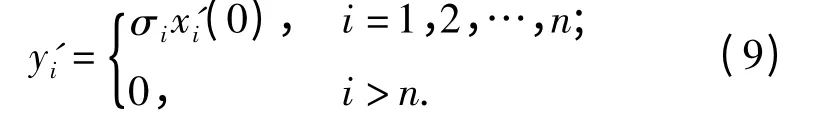
当σi较大时，相应的状态x'i(0)就能够以较大的增益传递到测量值，使测量值中能够包含较多的关于x'i(0)的信息，为x'i(0)的观测提供了有利的条件，即相应状态的可观性好。反之，如果σi较小甚至为0，状态x'i(0)的信息无法有效传递到测量值中，自然就无法从测量值中观测出相应的初始状态，即相应的状态可观性较弱或者不可观。

随着干部网络教育日渐发展壮大，学员人数增多，资源需求变大，技术要求更高，独立的干部网络教育部门很难兼顾所有工作，与第三方服务合作有助于更高效、更专业地开展工作。例如上海干部在线学习城就充分利用上海的信息服务行业，开展干部网络教育的外包服务工作，以课程制作为例，年度课程建设工作分为规划方创建计划、干教处组织审核、制作方制作课程、审核方审核课程、上线前干教处组织终审，再最终发布并运维课程，整个过程与投标并认证后的第三方服务单位开展紧密的合作，最终也取得了很好的效果。

因此，奇异值的大小能够有效地反应系统状态的可观性。奇异值越大，相应的状态(状态的线性组合)可观性越好。

然而，在很多情况下，奇异值直接表征的是系统状态线性组合的可观性，而无法直接表示系统中某个具体状态的可观性。根据前面的定义万德钧等［4］、刘百奇等［5-6］提出，将vi中的最大的元素所对应的系统状态xk(k∈［1，2，…，n］)与σi形成对应关系，用σi直接表征xk的可观性。这实际上是一种近似的做法，当vi中最大的元素远大于其他元素时，这种方法具有很好的近似程度。但是，当vi中的最大元素的优势不明显时，这种做法的合理性应该值得商榷。

实际上，对于很多不完全可观系统，通过正交变换，某个系统状态信息可能同时映射到可观性好的方向和可观性不好的方向。这里借鉴概率分布理论，假设状态xk(k∈［1，2，…，n］)的信息分别按照不同的概率μki(i∈［1，2，…，n］)映射到以X'(0)为基的状态空间中，即

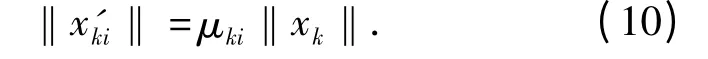
这里用状态的范数(模)表示状态信息，概率μki满足(11)式:

根据(9)式，状态xk的子信息的可观性与σi直接相关。因此，利用概率分布的平均值思想，用奇异值表征的状态xk的可观性就可以表示如下:

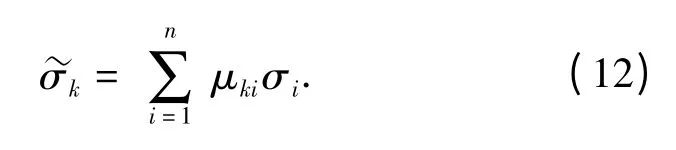
这样，通过~σk的大小就可以衡量状态xk的可观性。根据可观性矩阵的奇异值与可观性的关系，那些等效奇异值较大的状态对应的可观性较好，反之可观性较差。

2.2 弹载MEMS-INS 加GNSS 的组合效能分析

传统的炮射火箭弹均飞行在抛物弹道下，根据发动机的工作状态，可将弹道分为两个阶段:主动段和被动段;同时，根据制导与控制系统的作用，将火箭弹的飞行划分为有控和无控两种状态。下面利用2.1 节推导的基于等效奇异值的可观性分析方法，对某型炮射火箭弹无控和有控的典型弹道进行可观性分析。

搭载MEMS-INS/GNSS 组合导航系统的制导火箭弹，姿态测量精度往往是影响火箭弹制导精度的主要因素。因此，本文以火箭弹的姿态角为研究对象，分析在不同弹道条件下，3 个姿态角(滚转角γ、俯仰角ϑ、方位角ψ)的可观性。

前文在地理坐标系下，组建了以东、北、天失准角等作为状态的KF 系统。显然，这里的天向失准角φU与方位角误差Δψ 具有小角度下的等效关系。因此，只要分析天向失准角的可观测特性，就能够知道方位角的可观性。另外，为了能够直观地研究滚转角和俯仰角的可观特性，必须将上述的KF 方程进行结构变换，在其他状态变量不变的条件下，在准弹体坐标系下建立失准角状态方程。本文中，准弹体坐标系选取方式如下:坐标原点O 在导弹质心上，x 轴为弹体纵轴，指向弹头方向为正，y 轴在铅垂面内，与x 轴垂直，向上为正，z 轴与另外两轴构成右手坐标系。变换后的KF 状态变量如下:

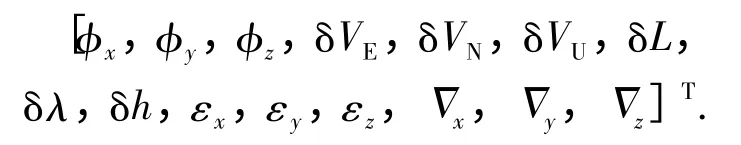
这样，x 轴失准角φx与滚转角误差Δγ 具有小角度下的等效关系，z 轴失准角φz与俯仰角误差Δϑ 具有小角度下的等效关系。这样，通过分析上述两种形式的KF 系统状态的可观性，就能够直接得到3 个姿态角的可观性。

可观性是系统在整个时域上的特性，表征的是系统利用包括当前时刻在内的所有已知观测值，估计初始状态的能力。由于系统参数在整个弹道上具有慢变的特性，所以在组合时间点，将系统参数冻结，视为线性定常系统，然后单独分析此段的可观性。这样就等同于将系统的初始时刻按照滤波节奏不断地进行顺延，只分析当前滤波时段的可观性。这种处理方式对于状态反馈式组合导航系统来讲具有合理性。

3 种典型弹道分别为无控弹道、俯仰机动弹道和偏航机动弹道。有控弹道的机动时间段均在10 ～24 s 之间，机动过程的横向过载曲线如图2 所示。利用等效奇异值法分析得到的3 个姿态角误差Δγ、Δϑ、Δψ 在不同弹道条件下的可观性如下:

1)滚转角误差Δγ 的可观性如图3 所示，从中可以看出，在弹体没有发生机动时，Δγ 的等效奇异值很小，接近于0，因此，在这些情况下Δγ 是不可观的，如果不考虑噪声的影响，卡尔曼滤波器不能正确估计出Δγ. 当载体产生机动时，随着法向过载的增大，Δγ 的可观性明显增大，从理论上来讲，这些时段卡尔曼滤波器应该能够对Δγ 进行正确的估计。

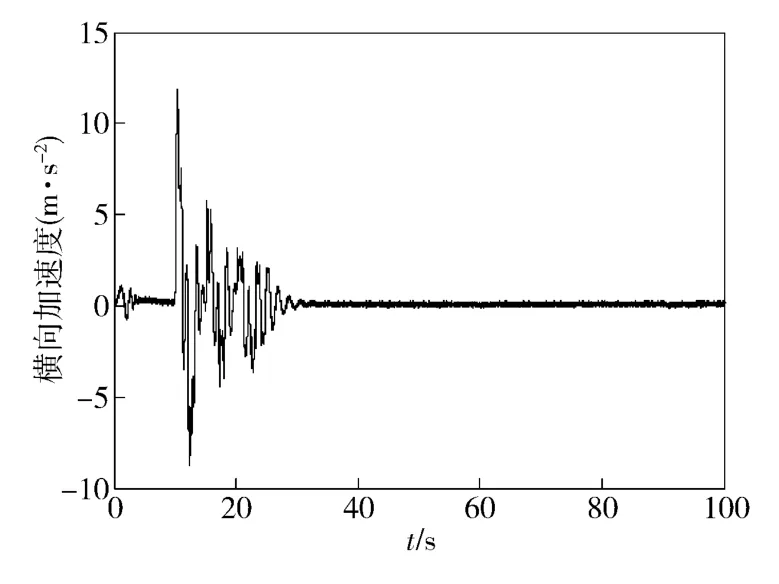
图2 有俯仰或者偏航机动时的横向加速度Fig.2 The acceleration curve during pitch or yaw maneuvering

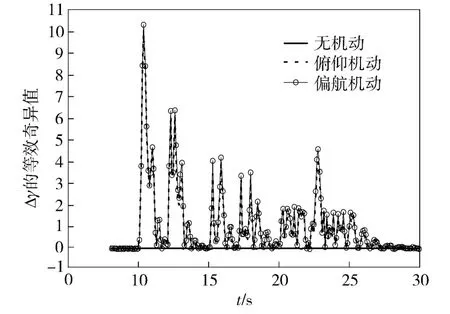
图3 用等效奇异值表示的Δγ 的可观性变化曲线Fig.3 The observability curves of Δγ

2)俯仰角误差Δϑ 的可观性如图4 所示，从中可以看出，Δϑ 在飞行全程都有较大的等效奇异值，俯仰机动会在一定程度上增大Δϑ 的可观程度。由于炮射火箭弹的弹道特性，在飞行全程，加速度主要分布在弹体纵轴上，通过分析图4 中的曲线，Δϑ 的可观性基本上与轴向加速度呈正比。

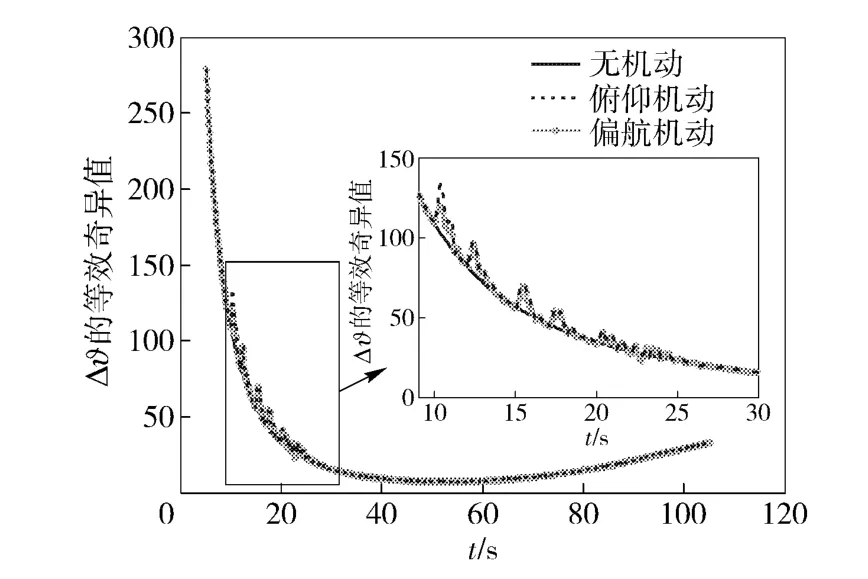
图4 用等效奇异值表示的Δϑ 的可观性变化曲线Fig.4 The observability curves of Δϑ

3)方位角误差Δψ 的可观性如图5 所示，Δψ的可观性基本上与Δϑ 类似，偏航机动会增加Δψ的可观测程度，而俯仰机动对Δψ 的影响则与弹体俯仰角存在一定的关系。

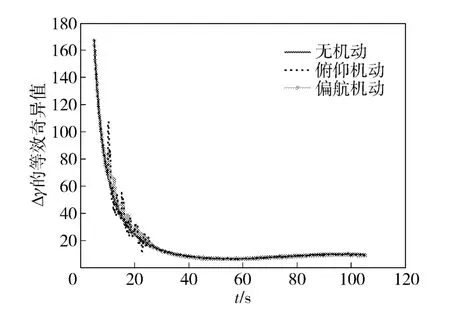
图5 用等效奇异值表示的Δψ 的可观性变化曲线Fig.5 The observability curves of Δψ

从以上的分析可以发现，垂直于Euler 角方向的加速度越大，相应的Euler 角偏差的可观性也就越好。

3 仿真分析

利用上述3 种弹道，进行组合导航分析，通过在相应的姿态角上人为施加一定的偏差，然后，考察组合系统对姿态偏差的估计情况，仿真条件如下:

无控飞行弹道的总时间为106.8 s，有控飞行比无控飞行时间短1 s，弹体机动的时间段为10 ～22 s.主动段持续时间为4.5 s，不进行组合导航解算。在5 s 时刻，分别在相应的姿态上人为加入5°的姿态角误差，从5.1 s 开始进行组合导航，每0.1 s 一个节拍，卡尔曼滤波器进行测量更新，然后，将所有状态的最优估计值反馈到MEMS-INS 系统中进行校正。3 种弹道条件下的姿态角误差滤波结果如下:

1)滚转角偏差Δγ 在不同弹道下的滤波结果如图6 所示，从图中可以发现，在弹体没有机动时Δγ 几乎不收敛，当弹体开始机动时，Δγ 则能迅速收敛。这与前面分析的滚转角误差的可观性是一致的。

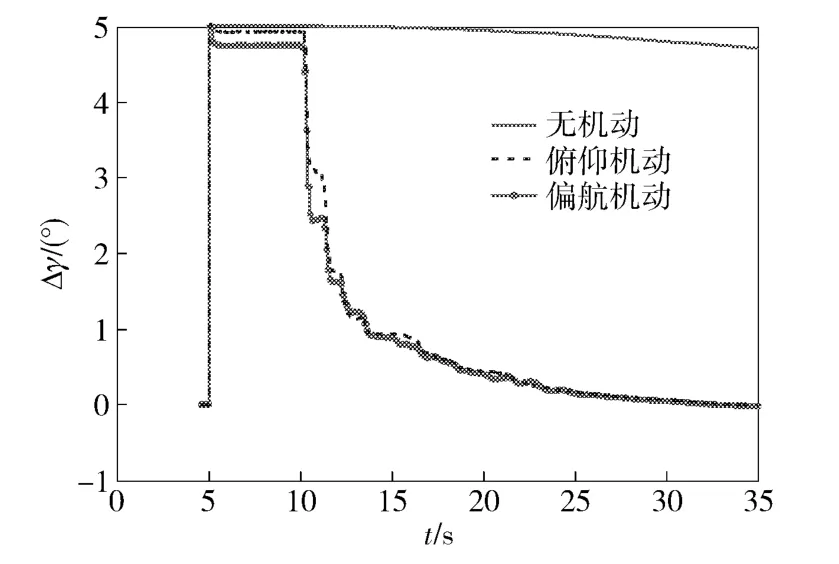
图6 3 种弹道下Δγ 的最优估计结果Fig.6 Δγ curves in three trajectories

2)俯仰角误差Δϑ 在不同弹道下的滤波结果如图7 所示。Δϑ 在组合开始的几个节拍内迅速收敛。在前面分析Δϑ 的可观性时发现，由于弹道初始段轴向加速度较大，Δϑ 的可观性较好，当弹体轴向加速度减小时，Δϑ 的可观性也开始变差。同时，在最初的迅速收敛之后，Δϑ 又开始缓慢变大，这与系统建模的误差也有一定的关系。当弹体有俯仰机动时，Δϑ 的发散会得到抑制(如图7 中点划线所示)。

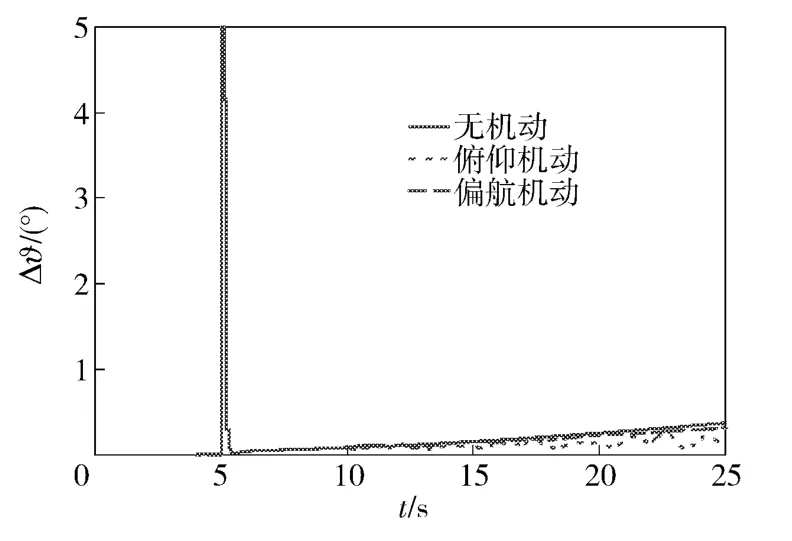
图7 3 种弹道下Δϑ 的最优估计结果Fig.7 Δϑ curves in three trajectories

3)方位角误差Δψ 在不同弹道下的滤波结果如图8 所示。与Δϑ 类似，Δψ 很快收敛，但是却出现了类似于控制系统中的超调现象。另外，在仿真中发现，当Δψ 快速收敛过程中，Δγ 会增大，增大的速度与Δψ 收敛的速度呈正比。也就是说，在只存在轴向加速度的情况下，Δψ 的估计会带来Δγ 的错误估计。这是因为，在这种情况下不存在法向加速度，Δγ 本身的可观性较弱，同时，在仿真中，方位角误差收敛时，俯仰角为35°左右，此时，滚转角与方位角存在动态耦合，Δψ 的变化会引起Δγ 的错误估计。这种现象如图9 所示，从图中可以发现，如果弹体发生机动，则由于错误估计导致的滚转角偏差会收敛，这与之前分析的滚转角可观性规律相符。

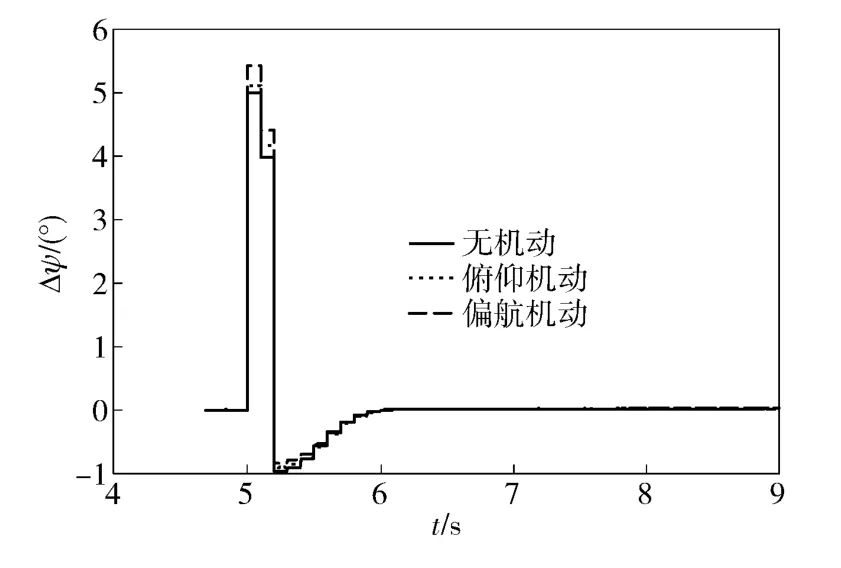
图8 3 种弹道下Δψ 的最优估计结果Fig.8 Δψ curves in three trajectories

图9 由于角度动态耦合引起的Δγ 的错误估计Fig.9 Fault estimation of Δγ caused by coupling with azimuth

4 结论

在奇异值法分析可观性的基础上，定义了状态等效奇异值这一概念，来作为系统状态可观性的度量标准。应用此方法，重点分析了炮射火箭弹的姿态角误差在典型弹道下的可观性变化趋势，仿真结果与可观性的分析结果具有一致性。

通过分析以及仿真，对于炮射火箭弹飞行时姿态角误差的可观性，可得到如下结论:俯仰角误差的可观性主要受轴向过载的影响，轴向过载越大，可观性越好;方位角误差的可观性则与弹体的水平过载直接相关，水平过载越大，可观性越好;滚转角误差则只与弹体的法向过载相关，法向过载越大，可观性越好。最后得到一致结论:垂直于Euler 角方向的加速度越大，相应的Euler 角偏差的可观性越好。

References)

［1］Maessen D C，Gill E K A. Relative state estimation and observability analysis for formation flying satellites［J］. Journal of Guidance，Control，and Dynamics，2012，35(1):312 -326.

［2］Meskin G，Itzhack B. Observability analysis of piece-wise constant systems［J］. IEEE Transactions on Aerospace and Electronic System，1992，28(4):1056 -1075.

［3］Kong Xingwei，Guo Meifeng，Dong Jingxin. An improved PWCS approach on observability analysis of linear time-varying system［C］∥Proceedings of 2009 Chinese Control and Decision Conference. Guilin，China:IEEE，2009，761 -765.

［4］万德钧，房建成. 惯性导航初始对准［M］. 南京:东南大学出版社，1998.WAN De-jun，FANG Jian-cheng. Initial alignment of inertial navigation［M］. Nanjing:Southeast University Press，1998. (in Chinese)

［5］刘百奇，房建成. 一种基于可观测度分析的SINS/GPS 自适应反馈滤波校正新方法［J］. 航空学报，2008，29(2):430 -435.LIU Bai-qi，FANG Jian-cheng. A new adaptive feedback Kalman filter based on observability analysis for SINS/GPS［J］. Acta Aeronautica et Astronautica Sinica，2008，29(2):430 - 435.(in Chinese)

［6］刘百奇，房建成. 一种基于可观测度分析的SINS/GPS 空中对准新方法［J］. 系统仿真学报，2008，20(16):4302 - 4305，4348.LIU Bai-qi，FANG Jian-cheng. Novel in-flight alignment based on observability analysis for SINS/GPS［J］. Journal of System Simulations，2008，20(16):4302 -4305，4348. (in Chinese)

［7］施桂国，周军，葛致磊. 基于无迹卡尔曼滤波的巡航导弹地磁自主导航方法［J］. 兵工学报，2008，29(9):1088 -1093.SHI Gui-guo，ZHOU Jun，GE Zhi-lei. Geomagnetic autonomous navigation technology of cruise missile based on the unscented Kalman filter［J］. Acta Armamentarii，2008，29(9):1088 -1093.(in Chinese)

［8］宋峰，张奕群. 星光大气折射观测导航方法可观性研究［J］.现代防御技术，2012，40(2):65 -70，81.SONG Feng，ZHANG Yi-qun.Research on observability of navigation approach using starlight refraction measurements［J］. Modern Defence Technology，2012，40(2):65 -70，81. (in Chinese)

［9］Feng Zhihua，Jiang Weiwei. Research of rapid transfer alignment and observability analysis［C］∥2nd International Conference on Intelligent Control and Information Processing (ICICIP). Harbin，China:IEEE，2011:204 -207.

［10］Lu Hongqian，Li Mingming. Observability of Geomagnetism/GPS/SINS integration during maneuvers［C］∥2011 3rd International Conference on Advanced Computer Control (ICACC 2011). Shanghai，China:IEEE，2011:604 -609.

［11］LIU Zhiping，YU Fan. Observability analysis and simulation of integrated navigation system during maneuver［C］∥The 30th Chinese Control Conference. Yantai，China:Shandon University and Yantai University，2011:3679 -3682.

［12］Sinpyo Hong，Man Hyung Lee. Observability of error states in GPS/INS Integration［J］. IEEE Transactions on Vehicular Technology，2005，54(2):731 -743.

［13］芦佳振，张春熹，彦廷洋. 应用卡尔曼滤波的线性系统可观测度实时估计算法［J］. 宇航学报，2009，30(3):982 -987.LU Jia-zhen，ZHANG Chun-xi，YAN Ting-yang. A real time estimation method of degree of observability for linear system using Kalman filter［J］. Journal of Astronautics，2009，30(3):982 -987. (in Chinese)

［14］Li Maodeng，Wang Dayi. Study on the observability analysis based on the trace of error convariance matrix for spacecraft autonomous navigation［C］∥10th IEEE International Conference on Control and Automation (ICCA). Hangzhou，China:IEEE，2013:95 -98.

［15］Bageshwar V L，Demoz G E，Garrard W L，et al. A stochastic observability test for discrete-time Kalman filters［J］. Journal of Guidance，Control，and Dynamics，2009，32(4):1356 -1370.

［16］Sinpyo Hong，Ho-Hwan Chun. Observability measures and their application to GPS/INS［J］. IEEE Transactions on Vehicular Technology，2008，57(1):97 -106.

［17］Tang Yonggang，Wu Yuanxin，Wu Wenqi. INS/GPS integration:global observability analysis［J］. IEEE Transactions on Vehicular Technology，2009，58(3):1129 -1142.

［18］Titerton D H，Weston J L. Strapdown inertial navigation technology［M］. 2nd ed. UK:The Institution of Electrical Engineers，2006.