逐发瞄准火炮的击发频率特性分析

王向民,姚兴太,王军,郭治

(1.南京理工大学自动化学院,江苏南京 290014;2.中国白城兵器试验中心,吉林白城 137001）

逐发瞄准火炮的击发频率特性分析

王向民1,姚兴太2,王军1,郭治1

(1.南京理工大学自动化学院,江苏南京 290014;2.中国白城兵器试验中心,吉林白城 137001）

针对逐发瞄准的火炮,在射击诸元误差为均方可导、各态历经的正态过程假定下,给出了射击诸元误差对椭圆射击门随机穿越周期的分布特性;在火炮存在射击准备(后坐、复进、装填、瞄准)时间的约束下,导出随机射频的分布特性,给出平均射频的解析表达。通过仿真示例和实验数据分析,验证了对平均射频分析的有效性和实用性。该研究为逐发瞄准武器系统的射击频率的论证、设计和检测提供了分析工具。

兵器科学与技术;逐发瞄准;射击门;随机穿越特性;击发频率

0 引言

逐发瞄准的火炮射频的均值是火力反应速度的关键性指标,它已被纳入战术技术指标体系。然而,有关这种体制下对随机射频的统计特性分析的文献却很鲜见,文献[1-3]主要研究的是首穿问题和滞留时间问题,其利用了大偏差理论,要求噪声方差无限小,因而并不适用于射击过程。文献[4]分析了各态历经的正态序列对具有矩形射击门的随机射频,它虽然给出了射击诸元误差必须在射击门内滞留一段时间后才允许射击的约束条件,但却未能引入两次射击时间必须大于射击准备(后坐、复进、装填、瞄准)时间这一必要的约束。文献[5]在相似约束条件下,将文献[4]的结论扩展到各态历经正态过程。文献[6-7]利用文献[4-5]的成果,讨论了它们在坦克炮或高炮上的应用。然而上述文献均未讨论受射击准备时间限制的火炮随机射频的分布特性。本文针对逐发瞄准火炮的射击特点,假定火炮射击诸元误差为各态历经正态过程,给出了随机射频(其倒数为随机击发周期)的分布函数及其均值的数学表达式,以及均值的计算方法,最后通过示例,还昭示了平均射频与系统的结构参数间的定量关系,为论证、设计、检测逐发瞄准的武器系统的平均射频提供了数学分析工具。

1 问题的描述

对现代的自动火炮,特别是行进间射击的自动火炮,不论是车载还是舰载,虽都配置了稳定装置,也难使其射击过程中的随机振动达到需求的稳定程度。为解决这一问题,行进间射击的直瞄火炮均以其火控解算诸元为中心,而间瞄火炮则以其陀螺装置构建的复瞄器所保持的火控解算诸元为中心,设置一个射击门。如果射击门为椭圆,射击诸元误差对其随机穿越过程如图1所示。

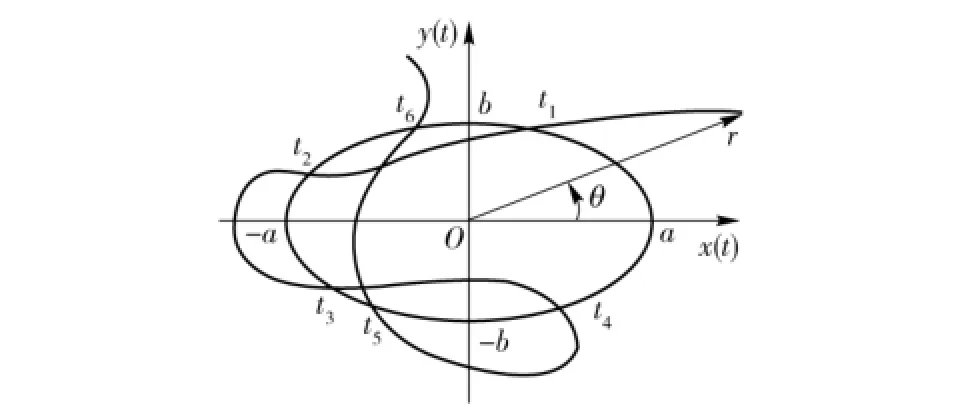
图1 射击诸元误差穿越椭圆射击门示意图Fig.1 Schematic diagram of firing data error passing through the elliptic shot area

图1中,坐标原点为火控解算射击诸元;以a、b为长、短半轴的椭圆为预置的射击门,记为Ω;Z(t)= [x(t),y(t)]T∈R2中的x(t),y(t)分别为火炮方位角、高低角对应的射击诸元误差;称t1,t3,t5,…为Z(t)对于射击门Ω的正(由外向内)穿越点,t2,t4, t6,…为Z(t)对于射击门Ω的负穿越点。

如果对Z(t)采用连续的检测装置(如自整角机或正余弦变压器),再考虑到火炮击发后,还需要上述的射击准备时间Tδ,为能尽快的自行生成击发指令,逐发瞄准体制下的火炮击发瞬时的选择准则应是:第一个正穿越点t1是首发击发瞬时;后一击发瞬时与前一击发瞬时所对应的两个正穿越点间的时间间隔是大于Tδ中的最小者。很显然,这里给出的逐发瞄准火炮的射频是随机的,它与射频为定值的高炮、机枪有明显的区别。

2 对射击门随机穿越强度

设Z(t)=[x(t),y(t)]T∈R2中x(t),y(t)为相互独立、各态历经、均方可导、零均值的正态过程。由随机理论知它们的均方导数x·(t),y·(t)也为零均值正态过程,且与其原函数相互独立。故有它们的联合密度函数

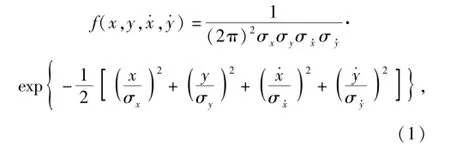
式中:σx、σy分别为x(t)、y(t)的均方差;σx·、σy·分别为(t)、(t)的均方差。

设射击门为椭圆,如图1所示,即

若做如下坐标变换:

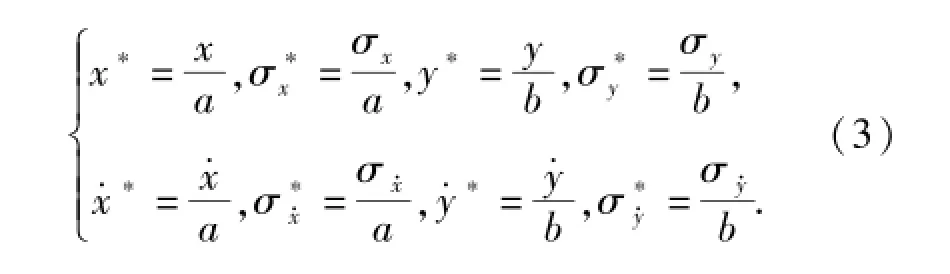
为了表达简洁,下面将删去经(3)式变换后带“*”号各量上的“*”号。此时,变椭圆射击门成单位圆,即x2+y2=1,如图2所示。

再做进一步的变换

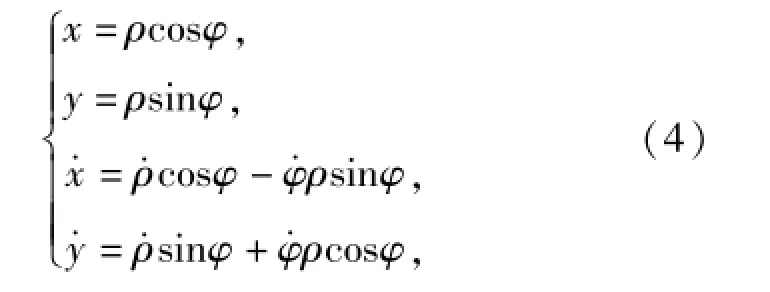
式中:ρ、φ分别为直角坐标系转换成极坐标的极径和极角,则变换后Z(t)的密度函数为

图2 变换后单位圆示意图Fig.2 Unit circle after transformation

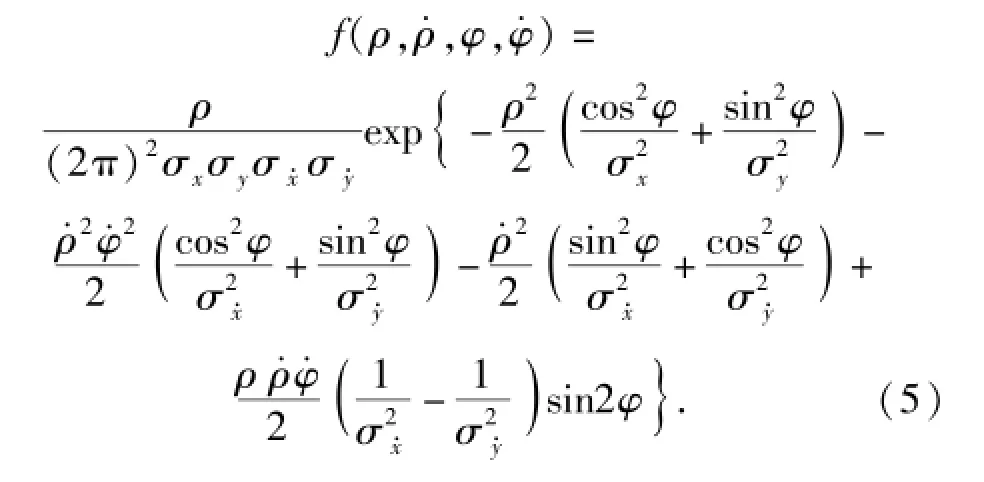
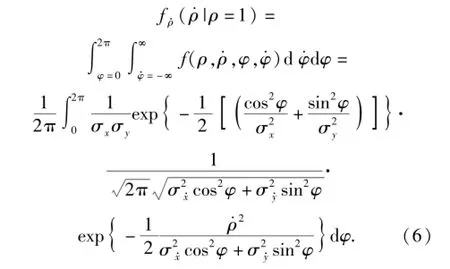
记λ为Z(t)在瞬时t对射击门单向穿越次数的均值,为与时间无关的常数,又称随机穿越强度,则有

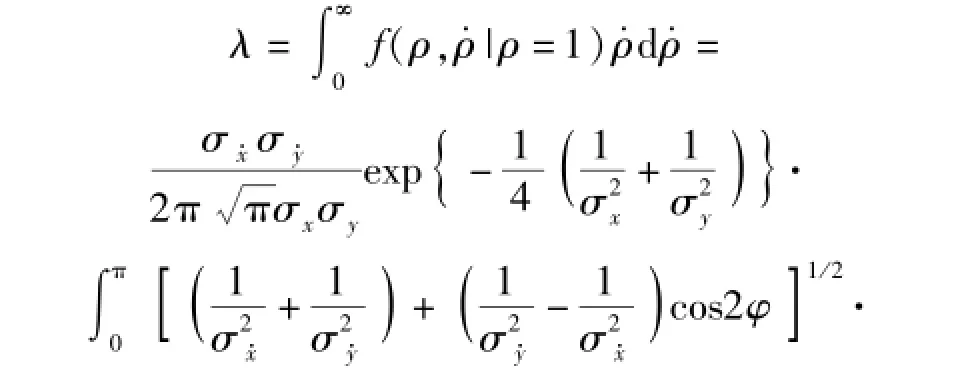
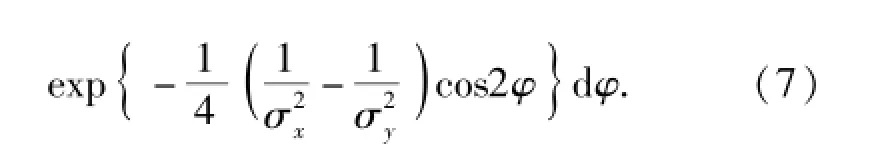
由于λ是一个重要参数,下面给出两个特殊条件下的表达式,即当σx·=σy·时,有

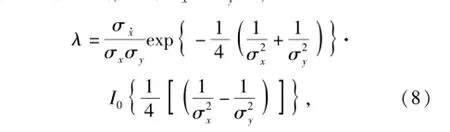
3 随机穿越周期

由文献[5]可知均方可导且各态历经的随机过程对射击域的随机穿越强度λ为时不变常数时,则:

1)单个滞留时间Tin=t服从指数分布

且该随机周期内的滞留时间和待机时间互相独立,其中

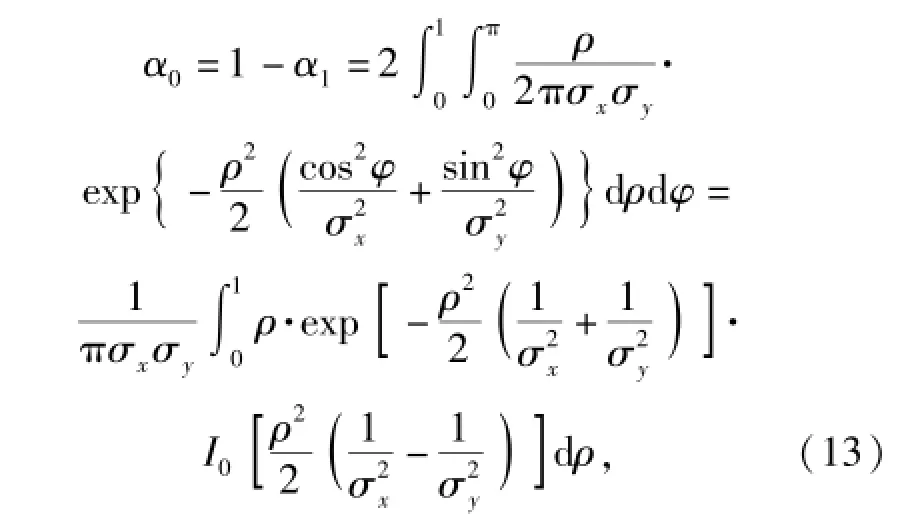
为射击诸元[x(t),y(t)]在射击门内的概率,而α1为其在射击门外的概率。

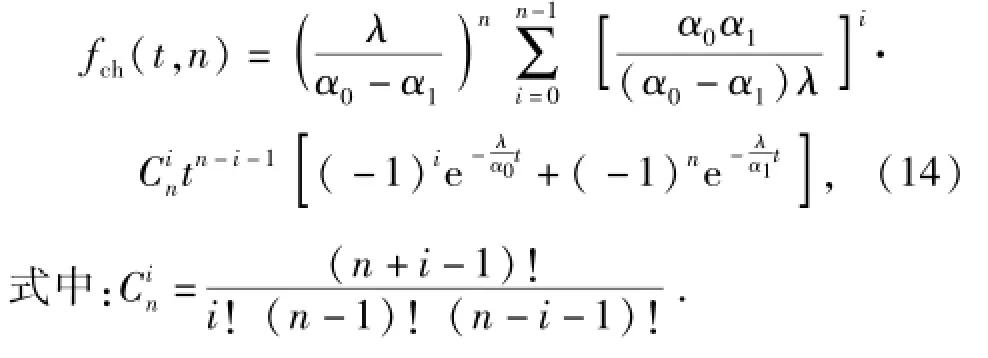
由于相互独立的n个连续随机变量和的密度函数等于它们密度函数的n-1次卷积,记*为卷积符号,考虑到滞留时间与待机时间都是相互独立的,故有

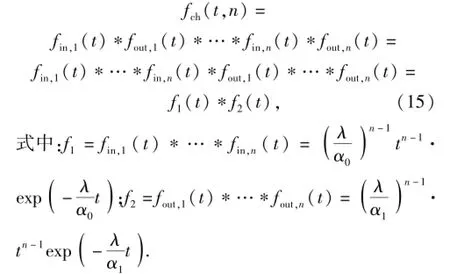
将f1和f2的表达式代入(15)式即为所求。

现对(14)式的含义做如下诠释:当n为常数时,它是n个周期长度之和、连续的密度函数;当t= Tσ为固定值时,它给出的是t∈(0,Tδ]区间内,出现n个随机周期的概率,为离散的概率分布函数。由于t=0∉(0,Tδ],故t=0这个正穿越点不属于第一个穿越周期,若n=0则表示在t∈(0,Tδ]区间内,不存在正穿越点。

4 逐发瞄准火炮的击发时间特性

当火炮射击诸元误差满足(10)式～(13)式的条件,且依前述之击发准则实施击发时,火炮的随机击发周期Tj的密度函数为

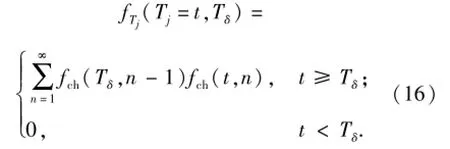
将图1中的所有穿越点依时间轴展开,如图3所示。

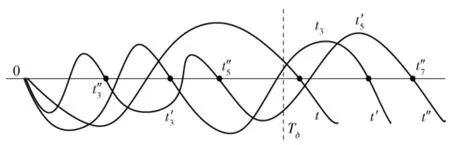
图3 穿越椭圆射击门展开示意图Fig.3 Elliptic shot area spreading out along the edge

图3给出了从t＞0点出发的3个可能的火炮射击诸元误差:它们分别表示在射击准备区间(0,Tδ]内出现n=0,1,2,3个正穿越点的4种情形,实际上,它们会依(14)式给出的概率出现更多的正穿越点。依前述的逐发瞄准射击准则,如果击发周期发生于第n个随机周期的终端,那么,这n个随机周期之和,即击发周期Tj,它的分布密度为fch(t,n), Tj=t≥Tδ.而上述事件等价于区间t∈(0,Tδ]内,必有n-1个随机周期,它发生的概率为fch(t,n-1).显然,如果击发周期Tj=t≥Tδ发生在第n个随机周期的终端,那么,它出现的概率密度应为fch(Tδ,n-1)· f(t,n),t≥Tδ.根据全概率公式,对fch(Tδ,n-1)· f(t,n)中n≥0的所有整数求和,即(16)式。

在满足(16)式的条件下,火炮的平均击发周期,依均值定义,有

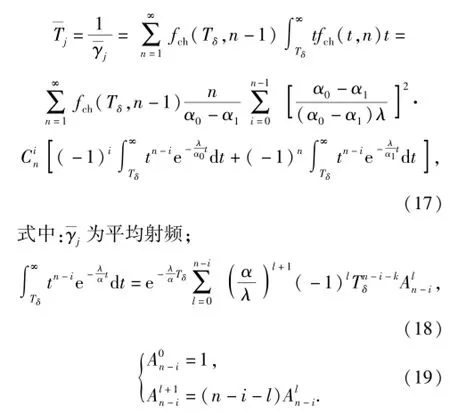
将(18)式、(19)式代入(17)式,即得平均射频的解析表达式。显然,(17)式为n、i、l三重循环计算式。由于在火炮射击准备时间Tδ内,火炮射击诸元误差的振动周期超过4次的概率极小。n通常取3～4之后即可终止计算,故(17)式虽繁,但计算的开销却可接受。在已知λ、α0、Tδ的条件下,可以由(16)式给出随机射频的密度函数的数字解,从而依定义直接计算更为简洁,但分析λ、α0、Tδ对平均射频的影响却不如(17)式方便。

5 示例

5.1 示例1

以不相关的两个正态白噪声分别通过传递函数为的成型滤波器,以其输出的不相关的各态历经函数x(t),y(t)作为在两个方向上的射击诸元误差的模拟量(设单位为mil),显然有[8]

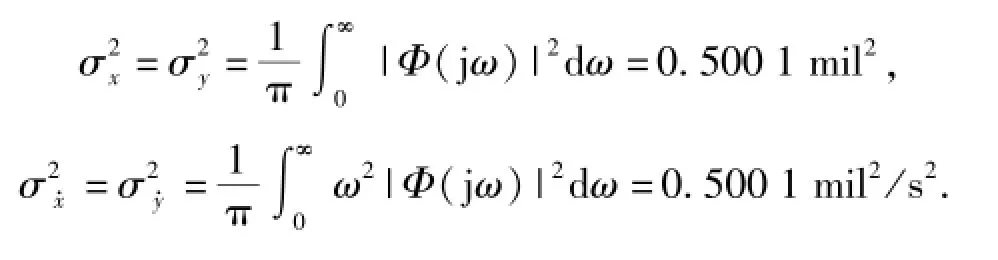
设射击门半径ρ=1 mil,则由(7)式知,射击诸元[x(t),y(t)]对射击门的随机穿越强度λ=0.2067 s-1.

再由(13)式求得:α0=0.135 3,α1=0.864 7.

若再设射击准备时间Tδ=0.8 s,则由(17)式可计算出平均击发周期和平均射频:

5.2 示例2

今有以40 ms采样周期的实测火炮射击诸元误差数据3组,分别整合成具有2 998个采样点、历时119.88 s的方位角x(k)、高低角y(k)曲线,如图4所示。

若取射击准备时间Tδ=1.9 s,椭圆形射击门:短轴a=1 mil;长轴b=1.768 mil.

利用Matlab中的统计工具箱,使用正态分布拟合的假设检验,x(k)与y(k)均以95%的置信度服从正态分布,并统计出相应的方差:σx=0.625 mil;σy=1.105 mil.

再用(13)式,可得:α0=0.083 2;α1=0.916 8.

利用各态历经正态过程x(t)的自然频率λx(在单位时间内,x(t)对其均值x(t)=0的正、负穿越点的个数之和,次/s)与其方差及导数的关系[8]

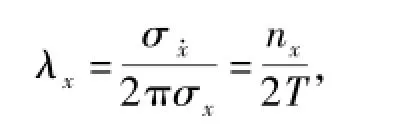
图4 处理后的火炮射击诸元误差数据Fig.4 The processed firing data errors

式中:T为采样总历时;nx为采样总历时内x(t)的正负穿越点的总数。根据图4中方位角和高低角射击诸元误差的数据可以分别统计它们穿越零均值的次数:nx= 61;ny=63.代入λx的计算式中可得: σx·=0.506 mil/s;σy·=0.913 mil/s.

利用(7)式与(17)式得到Z(t)对射击门随机穿越强度λ与平均射频

最后,从第一个正穿越点开始,依次检测并记录满足击发准则的正穿越点的个数(不含t=0时的正穿越点)n=11,故实际的射频

平均射频的理论计算值与实测值之差

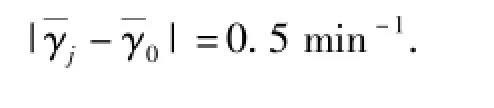
6 结论

为满足论证、设计、检验自动火炮平均射频这一新的战术技术指标的需求,本文以射击诸元误差对椭圆射击门的随机穿越特征量为工具,给出了随机射频的密度函数及其均值的解析表达式。示例1从射击诸元误差成型滤波器的传递函数出发,导出了相应火炮的平均射频,为论证和设计平均射频提供了工具;示例2从射击诸元误差的实测数据出发,通过对平均射频的理论计算与实测值之比较,既验证了平均射频计算公式的可信性,也为它的检测提供了方法。

由炮手直接操瞄的非自动火炮,它的瞄准镜不灵敏区的边界等效于射击门。坦克炮已有了现成的射击门,但其主要任务是提高首发命中率。如果在后续的射击过程中,要求提高它们的射速,(17)式将给出它们平均射速的最大值。

从(14)式、(16)式知,随机周期和射频的密度函数都仅取决于λ、α0、Tδ3个参数,对椭圆形状的目的域,只要已知上述3个参量,即可完成随机射频的分析,对研究随机射频具有普适意义。

References)

[1] Condamin S,Bénichou O,Tejedor V,et al.First-passage times in complex scale-invariant media[J].Nature,2007,450:77-80.

[2] Agnessa K.Control of a weakly perturbed Lagrangian system with a guaranteed escape rate[J].Probabilistic Engineering Mechanics,2011,26(1):39-43.

[3] Neumann M,Sze N S.On the inverse mean first passage matrix problem and the inverse M-matrix problem[J].Linear Algebra and Its Applications,2011,434(7):1620-1630.

[4] 王军,李玉山,张贤椿,等.具有射击域的武器系统的击发特性与精度[J].兵工学报,2010,31(2):144-148.

WANG Jun,LI Yu-shan,ZHANG Xian-chun,et al.The analysis on the shooting characteristics and precision for weapon system with shooting domain[J].Acta Armamentarii,2010,31(2):144-148.(in Chinese)

[5] 刘超,郭治,王远钢.机动目标在射击门下的概率模型估计[J].系统仿真学报,2008,20(3):697-701.

LIU Chao,GUO Zhi,WANG Yuan-gang.Estimate of probability models on maneuver object crossing shot door[J].Journal of System Simulation,2008,20(3):697-701.(in Chinese)

[6] 刘超,王军,郭治.一种基于滞留时间序列的毁伤率估计[J].兵工学报,2011,32(4):508-512.

LIU Chao,WANG Jun,GUO Zhi.An estimation method for kill probability based on random residence time series[J].Acta Armamentarii,2011,32(4):508-512.(in Chinese)

[7] 郑伟,王建斌,卢志刚.基于随机穿越特征量的射击门技术[J].火力与指挥控制,2010,35(增刊1):53-55.

ZHENG Wei,WANG Jian-bin,LU Zhi-gang.The firing gate technology based on the theory of random cut-through[J].Fire Control and Command Control,2010,35(S1):53-55.(in Chinese)

[8] 朱位秋.随机振动[M].北京:科学出版社,1992.

ZHU Wei-qiu.Stochastic vibration[M].Beijing:Science Press, 1992.(in Chinese)

Analysis on Firing Rate Characteristics of Duplicate-aim Artillery

WANG Xiang-min1,YAO Xing-tai2,WANG Jun1,GUO Zhi1
(1.School of Automation,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China; 2.China Baicheng Ordnance Test Center,Baicheng 137001,Jilin,China)

Under the assumption that the firing data error is a normal stochastic process of mean square differentiability and ergodicity,the distribution characteristics of stochastic passage period when firing data error passes through the elliptic shot area is given for the duplicate-aim artillery.While the preparing (recoil,counter-recoil,filling and aiming)time of artillery is taken into consideration,the distribution characteristics of random firing rate is deduced,and then the analytic expression for average firing rate is given.The practicability and effectiveness of average firing rate analysis are verified by the simulation examples and experimental data analysis.This research provides the analysis tool for proving,designing and detecting the firing rate of duplicate-aim weapon system.

ordnance science and technology;duplicate-aim;shot door;stochastic passage characteristic;firing rate

TP273

:A

1000-1093(2014)02-0158-06

10.3969/j.issn.1000-1093.2014.02.003

2012-08-06

国家自然科学基金项目(51109215、61104197);国家部委预先研究项目(4040507013)

王向民(1975—),男,助理研究员,博士研究生。E-mail:wangxiangmin@mail.njust.edu.cn;郭治(1937—),男,教授,博士生导师。E-mail:guozhi@mail.njust.edu.cn