悬垂弹射自适应底座附加载荷变化机理研究

任杰,马大为,仲健林

(南京理工大学机械工程学院,江苏南京 210094）

悬垂弹射自适应底座附加载荷变化机理研究

任杰,马大为,仲健林

(南京理工大学机械工程学院,江苏南京 210094）

自适应底座的附加载荷是悬垂弹射系统的重要设计参数之一。为研究自适应底座在悬垂弹射时附加载荷的产生与变化机理,建立了自适应底座附加载荷的数学模型,推导附加载荷的微分与积分表达式,获得影响附加载荷的主要因素:底座的内压强、上端面的水平投影面积、触地区域的水平投影面积。通过数值模型对附加载荷理论公式进行了验证,解析解与数值解吻合较好,相对误差最大不超过1.9%.依据附加载荷积分公式,研究积分区域与附加载荷表现形式之间的关系,结果表明:附加载荷的方向与积分区域类型存在对应关系,可能出现局部作用方向相反的情况。当地基下沉量不大或出现局部剪切破坏时,附加载荷有可能不变;而地基下沉量较大时,附加载荷的幅值和方向可能均会变化。

应用力学;悬垂弹射;自适应底座;附加载荷;变化机理

0 引言

悬垂弹射技术是一种新颖的导弹冷发射技术,适用于压缩空气式、燃气式和燃气-蒸汽式弹射动力[1-6]。自适应底座是实现悬垂弹射的关键部件,其力学特性严重影响了发射品质和性能。自适应底座产生的附加载荷是悬垂弹射系统的重要设计参数之一,直接关系到导弹弹射的成功与否,涉及发射装置动力匹配、响应特性、结构强度、随机发射和安全性等重要问题。目前,国内对自适应底座的结构设计与应用才刚起步,尚未建立反映其结构形式与附加载荷之间内在规律的数学模型,较多的是通过试验手段来检验自适应底座的工作特性[7],因此研究附加载荷的产生与变化机理,对冷发射技术的发展有重要意义。

为研究自适应底座附加载荷的产生与变化机理,首先需要建立附加载荷的数学模型,从数学上描述附加载荷。本文针对悬垂弹射中常见的S弯形结构的自适应底座开展研究,取壁面微元推导附加载荷的微分表达式与积分表达式,获取附加载荷的影响因素与变化规律;在此基础上,依据附加载荷积分表达式,研究积分区域与附加载荷表现形式的关系;最后,依据附加载荷积分表达式探讨地基下沉对附加载荷的影响,为进一步的研究与实际工程应用提供理论参考。

1 悬垂弹射中的附加载荷问题

1.1 悬垂弹射系统

如图1所示,悬垂弹射系统主要由导弹尾罩、初容室、弹射动力源以及自适应底座所构成,其中自适应底座是由帘线-橡胶复合材料多层复合而成的柔性功能构件。在悬垂弹射中,自适应底座对地面的刚度、坡度以及不平度适应性较好,能够大幅降低对发射场坪的要求,应用前景非常广阔。

图1 悬垂弹射系统Fig.1 Drape ejection system

发射装置起竖后,初容室和自适应底座悬离地面一定高度。弹射时,初容室内部的弹射动力源产生高压气体,在初容室内部形成高压。压力作用在导弹尾罩上为导弹弹射提供动力,作用在自适应底座上则会使底座产生膨胀变形,触地后将压力释放至地面。由于底座悬垂,作用在底座上的气体压力不能全部传递到地面上,通过试验发现,底座对初容室底部形成了载荷作用,一般称之为“附加载荷”。附加载荷是悬垂弹射系统自适应橡胶底座结构设计重要的输入参数,对弹射载荷匹配和发射平台稳定性有重要影响。

1.2 自适应底座工作原理

如图2(a)所示,弹射动力源未工作前,自适应底座内部无高压气体存在,底座内外均为标准大气压强,底座保持初始状态,不发生变形,与地面不接触。弹射动力源开始工作后,形成的高压气体迅速充入自适应底座内部,底座受内部压力作用开始膨胀,此时底座内部为高压气体,外部为标准大气压。内外压强均作用在底座壁面上,由于壁面厚度很薄(约为十几毫米),忽略壁面厚度不会影响自适应底座附加载荷的研究。研究时忽略壁面厚度,并将其受力状态简化为只受内部相对压强p的作用。在压强p的作用下,自适应底座发生膨胀变形,最后与地面接触,释放压力达到平衡状态,如图2(b)所示。自适应底座的附加载荷在压强p作用下产生,对底座上部固定端面形成作用力,作用力的方向可能向上,也可能向下。

图2 自适应底座状态简图Fig.2 Schematic diagram of adaptive base state

目前,国内在附加载荷产生机理研究方面尚未有文献公开报道。在当前的设计中,主要通过模拟初容室建压的联合空放试验来测量附加载荷,但联合空放试验费时、费力、成本高,无法完全模拟实际边界条件。也有研究人员通过建立有限元仿真模型来计算弹射过程的附加载荷[7],但由于缺乏理论支撑,仿真计算的有效性还需进一步确认。

2 附加载荷产生与变化机理研究

2.1 附加载荷微分表达式

在柱坐标系下对膨胀状态的自适应底座进行研究,首先建立柱坐标系(ρ,φ,z),坐标系原点O取在底座上端面中心处,z向垂直向上,如图3所示。ρ1为底座上端面在水平面上投影的矢径,ρ2为底座壁面最外缘到z轴的距离,ρ3为底座触地边缘到z轴的距离,底座触地边缘与上端面的距离为h.

图3 柱坐标系中的自适应底座Fig.3 Adaptive base in the cylindrical coordinate system

在内部气体压力的作用下,底座的底部与地面接触,地面对底座产生反作用力。在矢径为ρ3的区域上,内部压力与外部反作用力相互平衡,可知作用在该区域上的内部压力不产生附加载荷。自适应底座壁面受气体压力的垂直作用,可将压力沿底座的径向和垂向进行分解,如图2(b)所示,压力的径向分量使底座承受径向张力作用,垂向分量产生附加载荷。

膨胀后的自适应底座壁面为曲面,在曲面上取微元dA进行研究,将dA在柱坐标系(ρ,φ,z)中进行放大,如图4所示。

图4 柱坐标系中的dAFig.4 dA in the cylindrical coordinate system

压强p垂直作用在dA微元上,产生的压力dp为

dp的垂向分量dF即为附加载荷,dF表示为

式中:α为dA微元与z轴的夹角。

微元dA的面积可表示为

式中:β为微元边长夹角;dφ为dA微元在柱坐标系中对应的角度。

由于β角非常小,有式中:dl为微元dA的边长。

将(4)式代入(3)式中,可得

由(5)式和(1)式可得到dA区域的压力dp:

将dρ=dlsin α代入(7)式中,略去高阶微量,整理后得

(8)式即为dA微元受压力作用所产生的附加载荷的微分表达式。(8)式中不包含dz,表明微元受压产生的附加载荷与高度h无直接关系。

2.2 附加载荷的积分表达式

自适应底座膨胀后的壁面为光滑曲面,设光滑曲面为∑.由于∑与平行于z轴的直线交点有可能为两个,故引入矢径为ρ2的辅助平面∑3,∑3将光滑曲面∑分为∑1和∑2,∑1和∑2为分片光滑曲面,且∑1、∑2与任一平行于z轴的直线交点只有一个,则∑1和∑2的方程均为单值函数z=z(ρ,φ),∑1和∑2在与z轴垂直的水平面上投影区域分别为D1和D2,函数z=z(ρ,φ)在Dρφ上具有连续偏导数,被积函数f(ρ,φ,z)在光滑曲面∑上连续,首先将曲面投影到水平面上,将对面积的曲面积分化为积分区域上的二重积分。

(8)式为dA曲面微元的附加载荷微分表达式,对自适应底座的壁面进行积分即可得到附加载荷的积分表达式。积分过程中,根据被积函数及积分域的形状选择适当的积分次序,以便使计算尽可能简单。根据曲面积分的算法,有

同样,由(5)式和(2)式可得dA区域上压力的垂向分量dF:

(9)式为附加载荷的积分表达式,是变上下限积分,ρ1和ρ3均为变量。ρ1为自适应底座上端面在水平面上投影的矢径,如上端面处于水平状态,则ρ1为定值,此时ρ1为上端面的内径,如图5(a)所示。

图5 积分区域的水平投影Fig.5 Horizontal projection of integral domains

ρ3与自适应底座触地的区域形状和大小有关,仅当地面水平时ρ3为定值,此时自适应底座触地区域与水平面平行,触地区域为圆形,ρ3为圆的半径。只有底座上端面处于水平状态,并且地面水平,积分表达式(9)式的上下限才有定值,如图5(b)所示。此时底座膨胀后的触地区域为圆形,(9)式可改写为

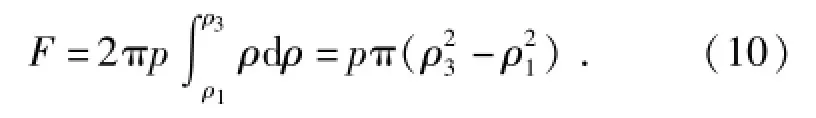
由(10)式可知,当自适应底座上端面与水平面平行,且地面水平时,自适应底座产生的附加载荷与内部压强p、上端面内径ρ1以及触地区域的半径ρ3有关。通常,自适应底座的内部压强p由导弹质量、弹射速度以及高度所决定。当自适应底座水平放置时,ρ1为上端面的内径,只有触地区域的半径ρ3能够发生变化,此时附加载荷只与底座触地面积有关。

为便于描述,将矢径ρ1包含的区域在水平投影设为D,区域D的面积设为S,矢径ρ3包含区域的水平投影设为D′,区域D′的面积设为S′,可将(10)式改写为

(11)式即为附加载荷的理论计算公式,可用来计算S弯型自适应底座在悬垂弹射时所产生的附加载荷。由上式可知,影响附加载荷的3个主要因素为压强p、上端面的水平投影面积S′、触地区域的水平投影面积S.

3 算例验证

为验证附加载荷积分表达式的正确性,建立S弯结构的自适应橡胶底座有限元模型[7],如图6所示。

图6 自适应底座有限元模型Fig.6 FEA model of adaptive base

自适应底座是由尼龙帘线-橡胶复合材料多层复合而成的柔性功能构件,其受压膨胀过程与气囊充气膨胀过程类似[8-9]。尼龙帘线-橡胶复合材料的力学特性较为复杂[10-13],需要采用基于细观力学的帘线-橡胶复合材料建模方法来建立自适应底座的有限元数值模型[14],对组分材料(尼龙帘线-橡胶材料)进行准确取值研究,考虑帘线股数对帘线拉伸性能的影响[15]。为使计算结果更具代表性,分别计算了9种工况,帘线弹性模量分别取0.7 GPa、0.8 GPa、1.0 GPa、2.0 GPa、2.5 GPa、3.0 GPa、3.5 GPa、4.0 GPa和5.0 GPa,不同的弹性模量所对应的底座变形程度不一致,触地区域也不相同。所有工况中底座上端面均保持水平,则S为定值,S= πρ21.而地面是倾斜的,坡度5%.

若已知p、S和S′,依据(11)式可计算相应的附加载荷。对于一个既定结构的自适应底座,p和S均已知,S′可以通过试验测得,也可通过仿真获取。本例中S′从仿真结果中获取,代入(11)式可得到附加载荷的解析解。数值解则由有限元软件对节点积分后得到。将计算结果进行无量纲化处理,如表1所示,负号表示附加载荷的方向向下。将仿真得到的数值解与解析解进行比较,以验证理论公式的正确性。表1中的相对误差是将两种解的差值与解析解相比后得到的。

表1 附加载荷的数值解与解析解Tab.1 Numerical solutions and analytical solutions ofadditional loads

表1中数值解与解析解吻合较好,误差最大为1.82%,出现误差的原因是有限元模型存在网格误差。取S′/S为横坐标,分别取无量纲化后的附加载荷解析解与数值解为纵坐标,绘制成曲线,如图7所示。

由表1和图7可知,附加载荷的解析解与数值解基本一致。这表明,自适应底座的附加载荷计算公式是正确的。

4 积分区域与附加载荷表现形式

4.1 积分区域

图7 附加载荷的解析解与数值解Fig.7 Numerical solutions and analytical solutions of additional loads

导弹弹射时,在瞬时强冲击载荷作用下,发射装置将会出现较大的晃动,使得自适应底座的上端面与水平面不再保持平行,而底座的触地区域也在时刻发生变化,导致其在水平投影面积S′也在不停变化,(9)式的积分上下限均不能确定,使得附加载荷存在多种表现形式。又由(11)式可知,区域D和D′的关系以及S和S′的大小对附加载荷F有很大的影响,通过分析发现,附加载荷存在以下5种表现形式:

1)若D⊂D′,则S＜S′,附加载荷F为正值,方向向上。

2)若D=D′,则S=S′,附加载荷F为0.

3)若D⊃D′,则S＞S′,附加载荷F为负值,方向向下。

4)若D∩D′,且有S＜S′,如图8所示,虽然总的附加载荷F仍为正值,但局部附加载荷有正有负,由于附加载荷直接作用在初容室底部,使初容室同时受方向相反的力作用,初容室的受力不均将影响发射装置的响应特性,给弹射过程带来了额外扰动。

图8 D∩D′,S＜S′Fig.8 D∩D′,S＜S′

5)若D∩D′,且有S＞S′,如图9所示,附加载荷的情况与4)相类似,总的附加载荷F为负值,但局部的附加载荷的方向并不相同,同样会使初容室受力不均,影响发射装置的响应特性。

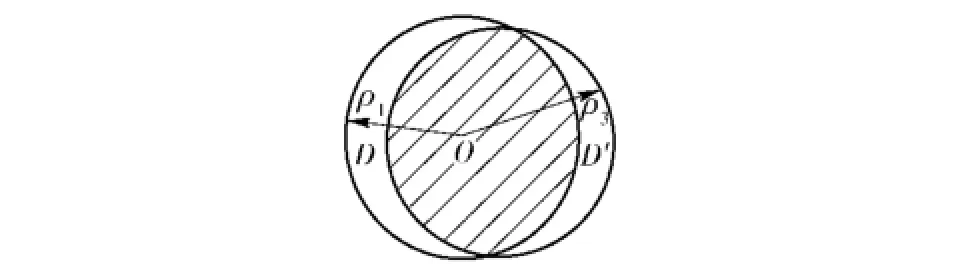
图9 D∩D′,S＞S′Fig.9 D∩D′,S＞S′

以上5类情况中,前3类情况在地面水平和地面倾斜时均会出现,后两类情况只出现在地面倾斜或者自适应底座的上端面与水平面不平行时。当地面存在倾斜时,如果在地面高点处自适应底座S弯的展开量在适应地面高度差后出现盈余,S弯处的壁面除了发生径向膨胀,还将有部分区域在压力作用下与地面发生接触,底座在地面高点处可能产生向上的局部附加载荷;而如果地面低点处自适应底座S弯的展开量不足以适应地面高度差,将会导致自适应底座底部的部分区域脱离地面,导致产生向下的局部附加载荷,最终形成两个方向相反的局部附加载荷,这种情况对初容室的受力与响应特性不利,应该予以避免。

4.2 地基下沉与附加载荷表现形式

在导弹弹射时,由自适应底座释放至地面的弹射载荷高达几十吨至上百吨,如在刚强度较差的地基上进行弹射,会导致地基出现下沉现象。一般认为地基的下沉会改变自适应底座的附加载荷,而依据本文的研究来看,既定结构的自适应底座工作时产生附加载荷仅与触地区域的水平投影面积直接相关。应根据地基下沉的类型来讨论其对触地区域水平投影的影响,再由触地区域水平投影的变化来判断对附加载荷产生的影响。

在弹射载荷作用下,地基的下沉类型主要有两种:一种为地基整体下沉,下沉区域大于底座触地区域;另一种为地基出现局部剪切破坏,也即仅底座触地区域内的地基出现下沉,触地区域外的地基不下沉。

第1种情况,地基整体下沉变相增大了自适应底座的离地高度,这种情况主要发生在表层刚强度较好而基础较薄弱的地基上。

1)如果地基下沉量不大,自适应底座S弯会通过调整壁面形状来适应路面的下沉而不影响触地区域的大小,即触地区域在水平面上的投影区域不会发生改变,则附加载荷不变。

2)如果地基下沉量较大,自适应底座S弯通过壁面形状的调整不能够完全适应离地高度的增大,则触地区域将会减小,此时附加载荷就会发生变化。如初始附加载荷向下,则地基下沉后附加载荷值将增大。如初始附加载荷向上,则地面下沉后附加载荷值将会减小,变为0,甚至可能出现反向的附加载荷。

第2种情况,地基出现局部剪切破坏,主要发生在刚强度较差的地基上,比如简易道路和砂石道路。这种情况下仅底座触地区域内的地基出现下沉,底座通过底部区域的拉伸变形来适应地基下沉,触地区域的水平投影不发生改变,由(11)式可知,附加载荷不发生改变。

5 结论

本文对悬垂弹射系统中自适应底座重要设计参数,即附加载荷的产生与变化机理进行了研究,得到了以下结论:

1)通过建立自适应底座附加载荷的数学模型,推导了附加载荷的微分表达式与积分表达式。在此基础上,获得附加载荷的理论计算公式。由理论公式可知,对充分膨胀后的自适应底座来说,附加载荷的大小与底座高度h无直接关系,影响其附加载荷的主要因素为:底座内部压强p、上端面在水平面上的投影面积S′、触地区域在水平面上的投影面积S.

2)为验证附加载荷理论公式的正确性,建立了自适应底座的有限元数值模型,数值模型中考虑自适应底座材料特性和地面倾斜。提取9种工况中附加载荷的数值解与解析解进行了比较,其相对误差最大不超过1.9%,吻合程度较好。

3)依据附加载荷积分公式,探讨了积分区域与附加载荷表现形式之间的关系,研究表明:5种不同的积分区域所对应的附加载荷作用方向均不相同,附加载荷值存在正值、零和负值3种情况,载荷作用方向也存在向上和向下两种,甚至存在局部作用方向相反的情况。5种类型的积分区域中,前3类情况在地面水平和地面倾斜时均会出现,后两类情况只出现在地面倾斜或者自适应底座的上端面与水平面不平行时。

4)探讨弹射过程中地基下沉对附加载荷的影响,对地基可能出现的下沉类型进行了细分。通过讨论可知,如果地基下沉量不大或出现局部剪切破坏时,底座的附加载荷值有可能不发生变化;如果地基下沉量较大,附加载荷值将会发生变化,附加载荷作用方向可能会出现反向的情况。

References)

[1] Spearman M L.Innovation in aerodynamic design features of soviet missiles,NASA 20080014230[R].US:NASA,2008.

[2] 芮守祯,邢玉明.几种导弹弹射动力系统内弹道性能比较[J].北京航空航天大学学报,2009,35(16):765-770.

RUI Shou-zhen,XING Yu-ming.Comparative studies of interior ballistic performance among several missile eject power systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009,35(16):765-770.(in Chinese)

[3] 杨风波,马大为,杨帆,等.高压弹射装置内弹道建模与计算[J].兵工学报,2013,34(5):527-534.

YANG Feng-bo,MA Da-wei,YANG Fan,et al.Interior ballistics modeling and calculation of high-pressure ejection device[J].Acta Armamentarii,2013,34(5):527-534.(in Chinese)

[4] 赵伟,阮健,李胜,等.液压弹射机构动力系统研究[J].兵工学报,2013,34(4):459-464.

ZHAO Wei,RUAN Jian,LI Sheng,et al.Research on power system of hydraulic catapult mechanism[J].Acta Armamentarii, 2013,34(4):459-464.(in Chinese)

[5] 刘上,刘红军,陈宏玉.富氧燃气发生器动态特性分析[J].航空动力学报,2013,28(1):226-232.

LIU Shang,LIU Hong-jun,CHEN Hong-yu.Analysis of oxidizerrich preburner dynamic characteristics[J].Journal of Aerospace Power,2013,28(1):226-232.(in Chinese)

[6] 肖虎斌,赵世平.燃气蒸汽式发射动力装置复杂内流场数值模拟[J].固体火箭技术,2009,32(4):392-395.

XIAO Hu-bin,ZHAO Shi-ping.Numerical simulation of the complex flow field in combustion gas-steam launching system[J]. Journal of Solid Rocket Technology,2009,32(4):392-395. (in Chinese)

[7] 刘琥,倪晓琛,白静.自适应底座悬垂弹射过程附加载荷分析[J].导弹与航天运载技术,2012(3):23-25.

LIU Hu,NI Xiao-chen,BAI Jing.Additional load study during the drape launch of adapting base[J].Missiles and Space Vehicles, 2012(3):23-25.(in Chinese)

[8] 卫剑征,谭惠丰,苗常青,等.空间折叠薄膜管的充气展开动力学实验研究[J].力学学报,2011,43(1):202-207.

WEI Jian-zheng,TAN Hui-feng,MIAO Chang-qing,et al.Experimental research of inflatable deployment dynamics of folded membrane booms[J].Chinese Journal of Theoretical and Applied Mechanics,2011,43(1):202-207.(in Chinese)

[9] 顾太平,何琳,赵应龙.囊式空气弹簧平衡性分析[J].机械工程学报,2011,47(3):69-72.

GUI Tai-ping,HE Lin,ZHAO Ying-long.Equilibrium performance analysis for bellows type air spring[J].Chinese Journal of Mechanical Engineering,2011,47(3):69-72.(in Chinese)

[10] Akangah P,Lingappa S,Shivakumar K.Effect of nylon 66 nanofiber interleaving on impact damage resistance of epoxy carbon fiber composite laminates,AIAA2009-2590[R].US:AIAA, 2009.

[11] Hu H T,Lin W P,Ke L S.Nonlinear analysis of fiber-reinforced composite laminates subjected to uniaxial compressive load, AIAA2013-1783[R].US:AIAA,2013.

[12] Xie Z M,Chai D L,Chen S C,et al.Effect of cord construction on the properties of rubber composites[J].Applied Mechanics and Materials,2013,328:906-910.

[13] Xie Z M,Chai D L,Du H W,et al.Interface parameters of composite materials with an elliptical cross-section fiber bundle[J]. Applied Mechanics and Materials,2013,275/276/277:1688-1692.

[14] Ren J,Zhong J L,Ma D W.A method of cord-rubber composite materials based on cord tensile modulus correction[C]∥2013 International Forum on Special Equipments and Engineering Mechanics.Nanjing:Nanjing University of Science and Technology, 2013:248-252.

[15] 姚穆.纺织材料学[M].北京:中国纺织出版社,2009.

YAO Mu.Textile materials[M].Beijing:China Textile&Apparel Press,2009.(in Chinese)

Research on Variation Mechanism of Additional Load of Adaptive Base during Drape Ejection

REN Jie,MA Da-wei,ZHONG Jian-lin
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

To research the formation and variation mechanism of the additional load,a mathematical model of the additional load is established,and the differential and integral formula of additional load are derived.The main factors which affect the additional load are obtained,such as pressure in adaptive base, horizontal projected area of upper face,and horizontal projected area of touchdown zone.The theoretical formula of additional load is verified by the numerical model.The analytical solution is well consistent with the numerical solution,and the relevant error is less than 1.9%.The relationship between the integral area and the expression form of the additional load is studied according to the integral formula of the additional load.The results indicate that there exists corresponding relationship between the direction of the additional load and the kind of the integral area,and that situation of that the direction is opposite in some areas may happen.When the ground subsidence is small or the shear failure exists in some area, the additional load may stays the same.When the ground subsidence is large,the amplitude and direction of the additional load may change.

applied mechanics;drape ejection;adaptive base;additional load;variation mechanism

V553.1

:A

1000-1093(2014)05-0670-06

10.3969/j.issn.1000-1093.2014.05.014

2013-08-22

国家自然科学基金项目(51303081);江苏省自然科学基金项目(BK20130761)

任杰(1982—),男,讲师。E-mail:renjie@njust.edu.cn;

马大为(1953—),男,教授,博士生导师。E-mail:ma-dawei@mail.njust.edu.cn